- Учителю
- Решение задач с помощью дробных рациональных уравнений. Алгебра (8-й класс)
Решение задач с помощью дробных рациональных уравнений. Алгебра (8-й класс)
Решение задач с помощью дробных рациональных уравнений. Алгебра (8-й класс)
Цель урока
- отработка навыков решения задач на составление дробных рациональных уравнений;
- знакомство с геометрическим способом решения уравнений;
- развитие способности к содержательному обобщению и рефлексии;
- развитие алгоритмического мышления;
- повышение интереса к решению математических задач
- показать связь с другими предметами, с жизнью.
Пусть математика сложна,
Ее до края не познать
Откроет двери всем она,
В них только надо постучать.
Чтобы двери в мир математики открывались как можно легче мы сегодня будем учиться… Чему?
Ребус этот разреши,
А ответ нам напиши
Сей ответ встречаешь часто,
Не решаешь их напрасно.
![]()
- Правильно, наш урок посвящен задачам, и не простым, а задачам на составление дробных рациональных уравнений.
I. Актуализация опорных знаний.
1. Большинство задач на составление дробных рациональных уравнений в результате сводится к решению квадратных уравнений. Большой вклад в решение уравнений внес французский математик - … Как его звали? -Франсуа Виет "вызывает вас на соревнование, предлагая для решения следующие уравнения:
(На экране и на партах уравнения)
- Как называются такие уравнения?
- С помощью какой теоремы решим данные уравнения?
- Какое свойство коэффициентов квадратного уравнения можно использовать при решений некоторых уравнений?
В-1
-
Х2 + 7Х +10 = 0
-
Х2- 19 Х+18=0
-
Х2+9Х+20=0
-
Х2-17Х+30=0
-
13Х2-29Х+16=0
-
17Х2-19Х-36=0
В-2
-
Х2 + 7Х-8 = 0
-
Х2+ 17Х-18=0
-
Х2-15Х+50=0
-
Х2+13Х+30=0
-
12Х2-35Х+23=0
-
100Х2+150Х+50=0
-
А сейчас поменяйтесь работами с соседом по парте, делаем проверку, выставляем оценку (ответы на экране) Собираем работы, чтобы я тоже могла посмотреть и выставить оценки.
-
2. Проверка домашнего задания с последующим использованием для углубленного изучения темы:
-
- нужно оформить решение домашней задачи № 610 на доске (1 ученик);
-
- а мы поработаем устно.
-
1) Верно ли решены уравнения?
-
А)
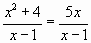 х1 =1, х2=4
х1 =1, х2=4
-
Ответ: нет, корень х=1 - посторонний.
-
Почему?
-
Б)
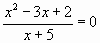 х=1
х=1
-
Ответ: нет, есть еще один корен Х=2.
-
Какой вывод нужно сделать?
-
2) Найти общий знаменатель дробей в каждом из уравнений:
-
Ответ: 5х-2 или 2-5х
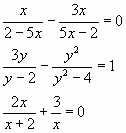
-
Ответ: у2-4
-
-
Ответ: х(x+2)
-
II. Поиск задач, математическими моделями которых являются дробные уравнения.
-
- Мы научились решать дробные уравнения.
-
А для чего они нужны? Какие задачи приводят к их появлению?
-
- Такие ,в которых одна величина выражается через другие при помощи дробного выражения.
-
Например: время =
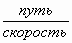 ;
;
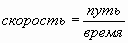 ;
;
-
Cторона прямоугольника=
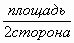 ;
;
-
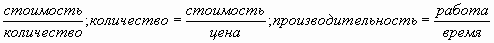 ;
;
-
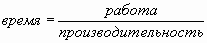 и другие.
и другие.
-
Итак, вы могли убедиться, что людям разных профессий приходится иметь дело с задачами на дробно-рациональные уравнения.
-
И на свете нет профессий
Вы заметьте-ка
Где бы нам не пригодилась Ма-те-ма-ти-ка! -
III. Решение задач + рисунок.
-
Проверим домашнюю задачу № 610. Поезд опаздывал на 1 час,чтобы приехать вовремя, увеличил скорость на 10 км/час на перегоне в 720 км. Найти скорость поезда по расписанию.720
-
Х
-
На самом деле
-
720
-
Х+10
-
72О
-
Х+10
-
-
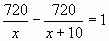 720х+7200-720х-х2-10х=0
720х+7200-720х-х2-10х=0
-
х 2 +10х-7200=0
-
Х1=80 х2= -90 (не удовлетворяет условию задачи).
-
80 км/час- скорость поезда по расписанию.
-
Ответ: 80 км/час.
-
Вы решили эту задачу алгебраическим методом. Я предлагаю решить используя геометрический метод
-
2. Геометрический метод.
-
Экскурс в историю. Геометрический метод решения задач появился во времена Евклида ( 3 век до нашей эры) и использовался не только в геометрии, но и в алгебре. Развивалась геометрическая алгебра. В старинных индийских сочинениях этого времени доказательство или решение сводилось к чертежу, подписанному одним словом "Смотри!". Решение алгебраической задачи геометрическим методом осуществляется в три этапа:
-
1) построение геометрической задачи, то есть перевод ее на язык геометрии,
-
2) решение получившейся геометрической задачи,
-
3) перевод полученного ответа с геометрического языка на естественный.
-
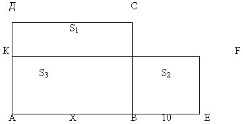
АВ=х -скорость поезда по расписанию (км/час).
-
АД - время движения поезда по расписанию (ч).
-
SАВСД = АВ х АД =720
-
Так как поезд увеличил скорость на 10 км/час, то прибавим к отрезку АВ отрезок ВЕ, условно изображающий 10 км/час. C увеличенной скоростью поезд прошел весь путь на 1 час быстрее, поэтому вычтем из отрезка АД отрезок ДК, условно изображающий 1 час.
-
S AEFK=SАВСД =720
-
S1+S3=S2+S3 -> S1=S2. S1 = Х и S2 =10 х EF.
-
Отсюда
-
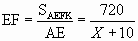
-
Получили, что
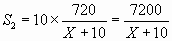 используя что S 1=S2 получим уравнение:
используя что S 1=S2 получим уравнение:
-
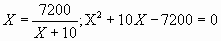
-
Решив это уравнен мы узнаем, что скорость поезда по расписанию была 80 км/час
-
Уравнения могут быть такими:
-
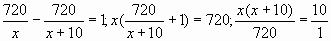
-
Обратите внимание, что переход к квадратному уравнению от первого и последнего уравнений осуществляется быстрее, чем в случае с другими составленными уравнениями.
-
IV.Физкультминутка (упражнение для глаз).
-
V. Задача ( ЕГЭ) В9.
-
Одна мастерская должна была изготовить 420 деталей, другая, за тот же срок 500 деталей. Первая выполнила свою работу на 4 дня раньше срока, а вторая на 7. Сколько деталей в день изготовляла вторая мастерская, если известно, что ежедневно она изготовляла на 5 деталей больше, чем первая?
-
- О чем идет речь в задаче? (О двух мастерских)
-
- Значит имеем: 1 и 2 мастерские
-
- Чем занимались эти мастерские ?
-
- Что спрашивается в задаче?
-
Пусть х (х>0)l деталей в день изготавливала П мастерская, тогда 1 изготавливала (Х-5) деталей в день. Сколько дней работала каждая мастерская?
-
- Какая из них быстрее справилась с работой?
-
- На сколько? (На 3 дня раньше чем 1 мастерская)
Получим уравнение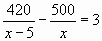 х(х-5)
х(х-5)
-
420х?-500(х-5)-3(х?-5х)=0
-
420х-500х +2500-3х?+15х =0
-
-3х? -65х -2500=0
-
Д=4225 +30000=34225=185?
-
Х 1 =
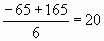
-
Х2=
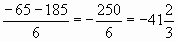 (не удовлетворяет условию задачи)
(не удовлетворяет условию задачи)
-
- Значит 2 мастерская изготавливала в день 20 деталей.
-
Ответ: 20 деталей.
-
VI. Домашнее задание: (заранее написать на доске) № 609.
-
(Придумать задачу по уравнению и решить ее
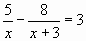 )
)
-
VII. Самостоятельно решить задачу № 615.
-

-
12(Х+10)+12Х-(х2+10Х)=0
-
12Х+120+12Х-х2-10Х=0
-
Х2 -14Х-120=0 Д=196+480=676=26? Х1=
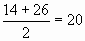
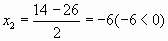
-
Один из рабочих выполнит работу за 20 дней, а другой за 30 дней. Ответ: 20 дней и 30 дней.
-
Итог урока: Общеизвестно высказывание: "Решение математической задачи можно сравнить со взятием крепости".
-
После данного урока решение большинства задач, я надеюсь,со взятием крепости уже не ассоциируется. Вы согласны со мной, ребята?
-
Математика всегда
-
То интересна, то сложна.
Получается задача -
Радуется душа. -
Пусть вам будут по плечу любые задачи. Успехов! Спасибо за урок!