Разработка урока 'Основное свойство алгебраической дроби' (8 класс)

Муниципальное бюджетное образовательное учреждение

«Средняя общеобразовательная школа №14»

Конспект урока по алгебре

в 8 классе

«ОСНОВНОЕ СВОЙСТВО АЛГЕБРАИЧЕСКОЙ ДРОБИ»

подготовила Вакалова Н.Н.,

учитель математики

высшей категории

НИЖНЕВАРТОВСК

2015

Основное свойство алгебраической дроби

Цели:

-повторение ранее изученного материала: основное свойство дроби;

-изучение основного свойства алгебраической дроби; рассмотреть примеры как сокращать дроби и приводить дроби к одинаковому знаменателю; закрепить умение применять основное свойство дроби;

-овладение знаниями и умениями, необходимыми для применения в практической деятельности,

-развитие памяти, речи, любознательности, познавательного интереса; формирование умений применять полученные знания в новой ситуации; развитие умственных операций (перенос знаний, сравнение, анализ)

-воспитание аккуратности, дисциплины; настойчивости в достижении цели; ответственного отношения к учёбе; воспитание взаимопомощи, культуры общения.

Ход урока

1. Организационный момент

Сообщить тему и цели урока.

2. Самостоятельная работа - 1

3. Объяснение нового материала

Слайд 2

Значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число.

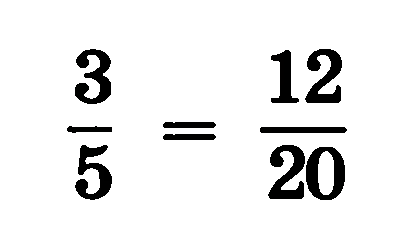
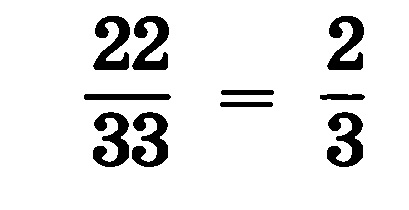
Слайд 3

Правила: основное свойство алгебраической дроби.

1. И числитель и знаменатель алгебраической дроби можно умножить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это - тождественное преобразование заданной алгебраической дроби.

2. И числитель и знаменатель алгебраической дроби можно разделить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это - тождественное преобразование заданной алгебраической дроби, его называют сокращением алгебраической дроби.

Слайд 4

Слайд 5

4. Закрепление нового материала

№ 2.3 (в); № 2.4(в,г); № 2.9(в,г); № 2.12(в,г); № 2.15(в,г); № 2.22(в,г);

№ 2.24(в,г); № 2.25(в,г)

V. Подведение итогов

VI. Домашнее задание:

§2. № 2.3 (а); № 2.4(а,б); № 2.9(а,б); № 2.12(а,б); № 2.15(а,б).

Информационные источники

1. Мордкович А.Г. Алгебра-8. Часть 1. Учебник.

2. Мордкович А.Г., Александрова Л.А., Мишустина Т.Н., Тульчинская. Алгебра-8. Часть 2. Задачник.

3. Александрова Л.А. Алгебра - 8. Самостоятельные работы / Под редакцией А.Г.Мордковича.