- Учителю
- Конспект урока алгебры для 9 класса 'Прогрессия вокруг нас'
Конспект урока алгебры для 9 класса 'Прогрессия вокруг нас'
Открытый урок в 9а классе по теме «Прогрессии вокруг нас».
Тип урока: комбинированный.
Цели урока:
1) образовательные:
- продолжить работу над определениями арифметической, геометрической прогрессий; формулами n-го члена, суммы n первых членов; характеристическими свойствами, которым обладают члены прогрессий; выработать общие рекомендации по выполнению заданий, содержащих данные прогрессии;
- убедится, что раздел математики «Прогрессии» являются неотъемлемой частью общечеловеческой культуры;
- продолжать формировать навыки применения прогрессии к решению прикладных задач;
- обобщить и систематизировать знания учащихся по данной теме.
2) воспитательные:
- содействовать воспитанию интереса к математике и ее приложениям, активности, умению общаться, аргументировано отстаивать свои взгляды.
3) развивающие:
- продолжить дальнейшую работу по выработке умения сравнивать математические понятия, находить сходства и различия, умения наблюдать, подмечать закономерности;
- учиться проводить рассуждения по аналогии; формировать умение строить и интерпретировать математическую модель некоторой реальной ситуации.
Ход урока:
1. Организационный момент:
Сегодня у нас заключительный урок по прогрессиям. Урок - подведения итогов нашей совместной проектной работы. На предыдущих уроках вы познакомились с возрастающими, убывающими, ограниченными, неограниченными последовательностями, но особое внимание удели двум последовательностям, каким?
Ответ: арифметическая и геометрическая прогрессия.
Что обозначает слово «прогрессия»?
Ответ: движение вперед.
Сегодня мы будем двигаться вперед и еще раз убедимся и убедим всех присутствующих в том, что…
- что раздел математики «Прогрессии» является неотъемлемой частью общечеловеческой культуры;
- прогрессия - это не просто математическая «игрушка», а мощный инструмент для решения реальных задач в различных сферах человеческой жизни;
- что знания о прогрессиях были известны еще в древнем мире;
- что знания по прогрессиям необходимы в банковских расчетах, в микробиологии и медицине, в строительстве и даже спорте.
Почти весь месяц мы всем классом готовили исследовательский проект по теме «Прогрессии». Дело в том, что основанием для этой работы послужили два момента: противоречия, возникшие между нами. Одни из нас считали, что прогрессии абсолютно не пригодятся в жизни, другие же были уверены в обратном. Второй момент заключается в том, некоторые задачи, предложенные нам для решения Аллой Вячеславовной, вызвали у многих из нас неподдельный интерес. Например, задача о мудром Сете, изобретателе шахмат, задача о финансовой пирамиде, задача о проторговавшемся покупателе лошади.
Мы назвали наш проект «Прогрессии вокруг нас».
Сформулировали основополагающий вопрос:
Прогрессия - это шикарная математическая «игрушка», или мощный инструмент для решения реальных задач в различных сферах человеческой жизни?
Проблемные вопросы
1. Какое практическое значение имеет факт размножения бактерий в геометрической прогрессии на жизнь на Земле?
2. Как используется факт размножения бактерий в геометрической прогрессии в пищевой промышленности, в медицине, в фармакологии, в сельском хозяйстве?
3. Когда скупой платит дважды?
4. Как богатеют банкиры?
5. Что знали о прогрессии люди, жившие несколько веков назад?
Учебные вопросы
1. Откуда к нам пришла арифметическая (геометрическая) прогрессия?
2. Что называется арифметической (геометрической) прогрессией?
3. Какими свойствами обладают арифметическая (геометрическая) прогрессии?
4. По какой формуле вычисляется n-ый член и сумма арифметической (геометрической) прогрессий?
Дальше разбились на 4 группы: историки, теоретики, микробиологи и экономисты. Каждая группа готовила теоретический материал и задачи в своем направлении. Весь полученный материал затем был проанализирован и синтезирован в текстовом носителе и в презентации. К тому же каждая группа подготовила красочный буклет с задачами на прогрессии по выбранной тематике.
2. Актуализация знаний:
Группа теоретиков собирала, анализировала и обобщала теоретический материал о прогрессиях, поэтому я обращаюсь в первую очередь к вам и ко всем с вопросами:
1. Какую прогрессию называют арифметической?
2. Какую прогрессию называют геометрической?
3. Почему арифметическую прогрессию называют арифметической? Сформулируйте ее характерное свойство.
(потому, что члены этих прогрессий находятся как среднее арифметическое для арифметической и среднее геометрическое - для геометрической прогрессии)
4. Для какой прогрессии записаны формулы слева? справа?
5. Назовите формулу n -го члена арифметической прогрессии. Что в формуле обозначает n? Какие значения он может принимать?
7. В чем состоит сходство между прогрессиями? А в чем есть отличия? ( сходство: есть формулы для нахождения любого члена прогрессии и суммы n первых членов прогрессии, прогрессии задаются по определенному правилу; различие: убывающая геометрическая прогрессия уменьшается гораздо стремительнее, чем арифметическая с одинаковыми исходными данными, и наоборот)
3. Устная работа:
1. Выбери последовательность, которая является арифметической прогрессией.
а) 34; 33; 31; 28; ...
б) 45; 15; 5; 14; ...
в) 12; 17; 22; 27; ...
г) 29; -28; 27; -26; ...
2. Найди разность арифметической прогрессии 45; 39; 15;… .
а) 15
б) -15
в) 2
г) 1/2
3. Последовательность (с ), задана формулой с
), задана формулой с =15-3n. Найдите с
=15-3n. Найдите с и c
и c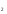 .
.
4. Определите знаменатель геометрической прогрессии ( а ), для которой а
), для которой а , а
, а .
.
5. Найдите седьмой член арифметической прогрессии, если а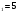 =12, а
=12, а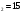 =16,5.
=16,5.
6. Определите знаменатель геометрической прогрессии ( а ), для которой а
), для которой а , а
, а
7. Окно расположено в трех метрах от двери класса. Сколько шагов мне необходимо сделать, чтобы выйти из класса, если первый мой шаг будет равен 1м, второй- 0,5м, третий - 0,25м и т. д. ?
8. Выбери последовательность, которая является геометрической прогрессией.
а) 1; 4; 9; 16;…
б) 23; 25; 29; 32;…
в) 1; 

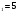
г) 2; 4; 12; 48;…
4. Решение задач:
Вами проведена большая исследовательская познавательная работа. Над проектом у нас работали четыре группы. Теоретики уже продемонстрировали свою работу. Теперь слово предоставляется группе историков. Они скажут несколько слов о появлении прогрессий и предложат нашему вниманию интересные исторические задачи на прогрессии.
Ученик: Термин «прогрессия» имеет латинское происхождение и был введен римским автором Боэцием в 6 веке. Сами названия «арифметическая» и «геометрическая» были перенесены на прогрессии из теории непрерывных пропорций, изучением которых занимались древние греки. В развитие теории о прогрессиях внесли свой вклад такие ученые, как Архимед, Пифагор и его ученики, французские математики Леонард Фибоначчи и Баше де Мезириак, немецкие математики М. Штифель, Н.Шюке и К. Гаусс.
Предание о царе Шераме и изобретателе Сете нам уже известно и задачу мы эту уже решали. Предложим вам две другие не менее интересные исторические задачи.
Задача №1 (из учебника Магнитского):
Богач-миллионер возвратился из отлучки необычайно радостный: у него была по дороге счастливая встреча, сулившая большие выгоды. Рассказывает он домашним: «Вот и на мою деньгу денежка бежит. Повстречался мне в пути незнакомец, из себя не видный. Предложил выгодное дельце, что у меня дух захватывает». «Сделаем,- говорит, - такой уговор. Я буду целый месяц приносить тебе ежедневно по сотне тысяч рублей. Недаром, разумеется, но плата пустяшная. В первый день я должен по уговору заплатить - смешно сказать - всего 1 копейку. А за вторую сотню тысяч - 2 копейки. И так целый месяц, каждый день вдвое больше предыдущего. Находим выгодность сделки.
Решение: Деньги, отданные богачом незнакомцу, составляют геометрическую прогрессию, например (b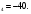 ). Тогда, b
). Тогда, b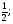 =1, b
=1, b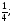 , b
, b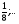 =4
=4  q= 2
q= 2
Богач-миллионер заплатил незнакомцу:
S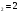 = 2
= 2 - 1 =10737418,23копеек
- 1 =10737418,23копеек  11 миллионов рублей.
11 миллионов рублей.
Незнакомец заплатил богачу: 30∙100 тыс = 3000 тыс. = 3000000 рублей.
Убыток 11000000 - 3000000=8000000 рублей.
Задача №2 (старинная еврейская задача)
На 10 братьев приходится  мины серебра. Брат над братом поднимается, на сколько поднимется не знаю. Доля восьмого - 6 шекелей. Брат над братом на сколько выше?
мины серебра. Брат над братом поднимается, на сколько поднимется не знаю. Доля восьмого - 6 шекелей. Брат над братом на сколько выше?
Решение: Необходимо знать, что 1 мина = 60 шекелям.
Здесь требуется по сумме первых 10 членов арифметической прогрессии, равной 100 шекелям и известному 8-му члену, определить разность арифметической прогрессии.
a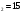 =a
=a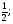 +7d
+7d  a
a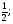 =6-7d
=6-7d

Ответ: d= -1,6.
Спасибо историкам. Пришла очередь экономистам показать, чем они занимались в рамках нашего проекта.
Ученик: Изучая материалы, связанные с прогрессиями, мы нашли большое количество задач с экономическим содержанием. Это задачи на банковские проценты на вклад, изменение оплаты труда и увеличение производства на предприятии, изменение цены товара и т. д.
Задача №3: Первоначальная цена товара на торгах повышалась несколько раз на одно и то же количество рублей. После третьего повышения цена равнялась 1200 р., а после двенадцатого повышения - 1650 р. Через сколько повышений первоначальная цена удвоилась?
Решение: (b )- арифметическая прогрессия, b
)- арифметическая прогрессия, b =1200; b
=1200; b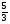 =1650;
=1650;



Так как цена товара увеличилась в два раза, то она стала равна 2100 рублей.
b = 2b
= 2b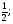 ; 2100 = 1050+50(n-1)
; 2100 = 1050+50(n-1)
50(n-1) = 1050
n-1 = 21
n = 20
Ответ: через 20 повышений.
Задача №4: В течение календарного года на автомобильном заводе «Фиат» зарплата каждый месяц повышалась на одно и тоже число долларов. За июнь, июль, август зарплата в сумме составила 9900 долларов, а за сентябрь, октябрь и ноябрь - 10350 долларов. Найдите сумму зарплат одного работника за весь год.
Решение: (b )-арифметическая прогрессия,
)-арифметическая прогрессия,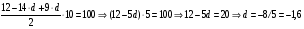 , а
, а 
Из этих двух равенств получаем систему уравнений и решаем ее:
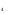
Теперь найдем суммарную зарплату работника «ФИАТА» за год:
S
Ответ: за год доход работника составил 39300 $.
Спасибо экономистам за хорошие задачи. Пришла очередь четвертой группы, группы микробиологов и медиков.
Ученик: Микробиология - наука о живых организмах, невидимых невооруженным глазом: , , микроскопические и , часто этот список продляют и . В область интересов микробиологии входит микроорганизмов, их , , , , роль в , а также возможности практического использования.
Эпиде́мия -- широкое распространение инфекционных болезней среди людей или среди животных, значительно превышающее обычно регистрируемый на данной территории уровень заболеваемости.
Задача№5: Человек, заболевший гриппом, может заразить четырех человек. Через сколько дней заболеет все население поселка в количестве 341 человека?
Решение: (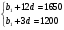 )- геометрическая прогрессия.
)- геометрическая прогрессия.
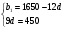 = 1; q= 4.
= 1; q= 4.
Найти 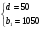 =341, где k - порядковый номер дня, когда все в поселке заболеют.
=341, где k - порядковый номер дня, когда все в поселке заболеют.
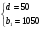 =
= 
341=1

 =341
=341
Так как, 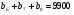 =256, а
=256, а 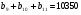 =1024, то человек заразит всех в поселке уже вначале 5-го дня .
=1024, то человек заразит всех в поселке уже вначале 5-го дня .
Ответ: 5 дней.
Ученик: Гомеопатия - терапевтический метод лечения, разработанный великим немецким врачом и ученым Самуилом Ганеманом (1755-1843). В основе гомеопатии лежит принцип подобия - вещество, способное в больших дозах вызывать определённые симптомы в организме, в малых дозах способно похожие симптомы лечить, т.е. подобное лечится подобным.
Задача №6: Больной принимает гомеопатическое лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день - на 5 капель больше, чем в предыдущий. Приняв 40 капель, он 3 дня пьет по 40 капель лекарства, а потом ежедневно уменьшает прием на 5 капель, доведя его до 5 капель. Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
Решение: (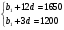 )- арифметическая прогрессия
)- арифметическая прогрессия
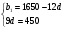 = 5
= 5
d=5
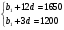 : 5, 10, 15,…,40, 40, 40, 35, 30,…,5
: 5, 10, 15,…,40, 40, 40, 35, 30,…,5
Найти :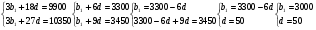 =180
=180
Решение : а = а1+d(n-1)
= а1+d(n-1)
40=5+5(n-1),
n=8
S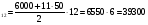
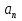
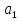 n
n
S8 = (5+40)·8:2=180 ; 180 капель больной принимал по схеме в первый период и столько же по второй период. Всего он принял 180+40+180=400 (капель), всего больной выпьет 400:250=1,6 (пузырька). Значит, надо купить 2 пузырька лекарства.
Ответ: 2 пузырька.
Ученик: Так как мы ограниченны во времени, то не можем показать все разнообразие задач по прогрессиям на одном уроке. Хочется лишь отметить, что задачи на прогрессии встречаются во многих сферах человеческой жизни. Прогрессии действительно везде вокруг нас. С помощью прогрессий можно проводить вычисления результатов в спорте, в компьютерной игре, решения физических и геометрических задач. Можно объяснить суть финансовых пирамид. Прогрессии существуют даже в литературе!
Спасибо всем группам за отличную работу и интересные задачи.
5. Рефлексия:
Работая над проектом, я понял…
Работая над проектом, я узнал…
Работая над проектом, мне понравилось…
Работая над проектом, меня порадовало…
Работая над проектом, я научился…
6. Подведение итогов.
Достигнуты ли цели нашего исследовательского проекта?
Понравилась работа над проектом?
Какие трудности были во время коллективной работы?