- Учителю
- Способ предоставления материала по теме Площадь многоугольника
Способ предоставления материала по теме Площадь многоугольника
Площадь многоугольника.
С темой «Площадь плоских фигур» учащиеся сталкиваются постоянно. Эта тема присутствует в заданиях ОГЭ и ЕГЭ, где нужно найти площади фигур напрямую, применяя формулы, и где необходимо разбивая фигуру на элементы. Учитывая этот момент и требования ФГОС, я вводила формулы нахождения площадей плоских фигур следующим образом.
Площадь параллелограмма.
При введении формулы площади параллелограмма я опиралась на имеющиеся уже знания обучающихся: формулы нахождения площади квадрата, прямоугольника и свойства фигур.
Раздала вырезанные фигуры параллелограмма и попросила разрезать
его так, чтобы получить новую фигуру, у которой можно найти
площадь. Ученики разбили ее таким образом.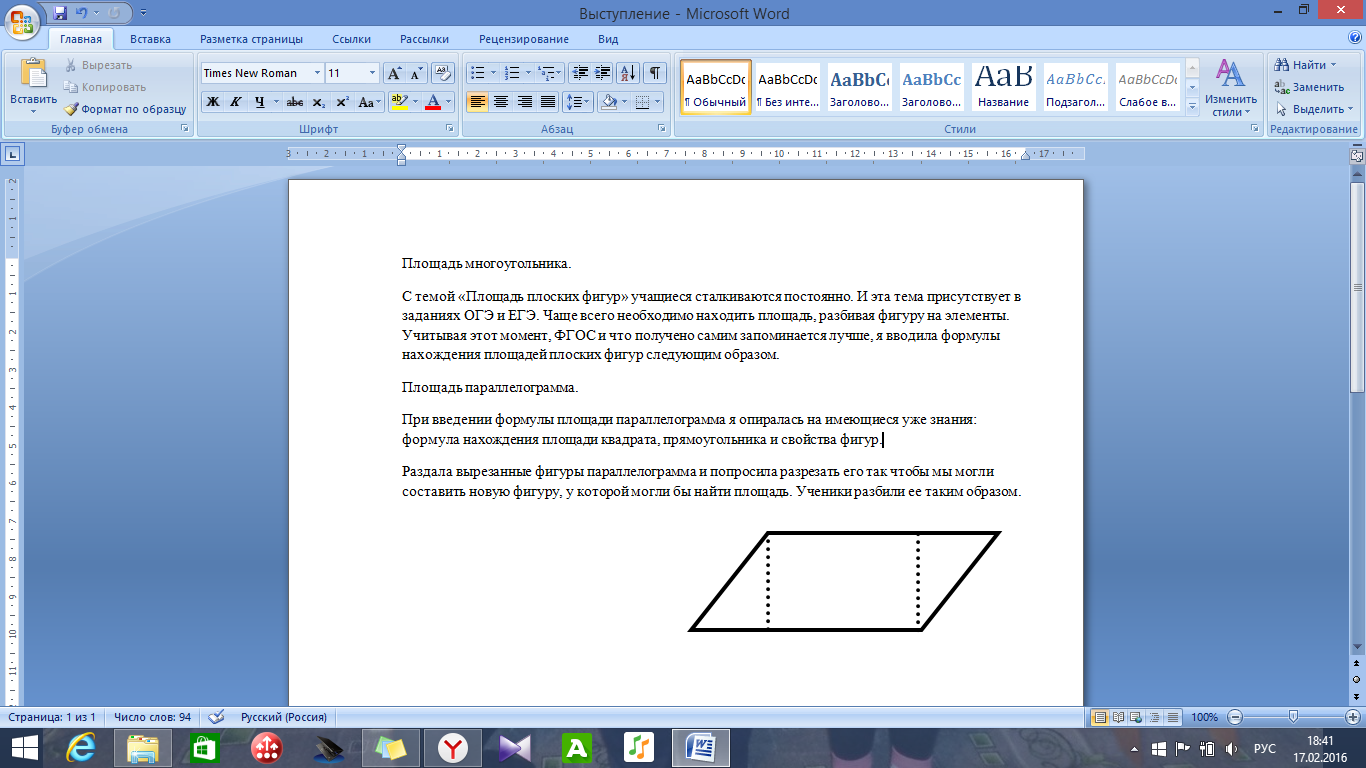
Далее проговариваем, что PB для параллелограмма является высотой. И делаем вывод, что площадь параллелограмма равна произведению высоты на сторону, к которой проведена эта высота.
Площадь треугольника.
Для нахождения площади треугольника опираемся на уже известную нам формулу - формулу площади параллелограмма.
В параллелограмме проводится диагональ, которая разбивает его на два равных треугольника. Равные фигуры имеют равные площади.
Вывод: площадь треугольника равна половине произведения высоты на сторону, к которой она проведена.
Площадь трапеции.
При изучении этой темы я предложила выбрать одну из трех разбивок трапеции и найти ее площадь.
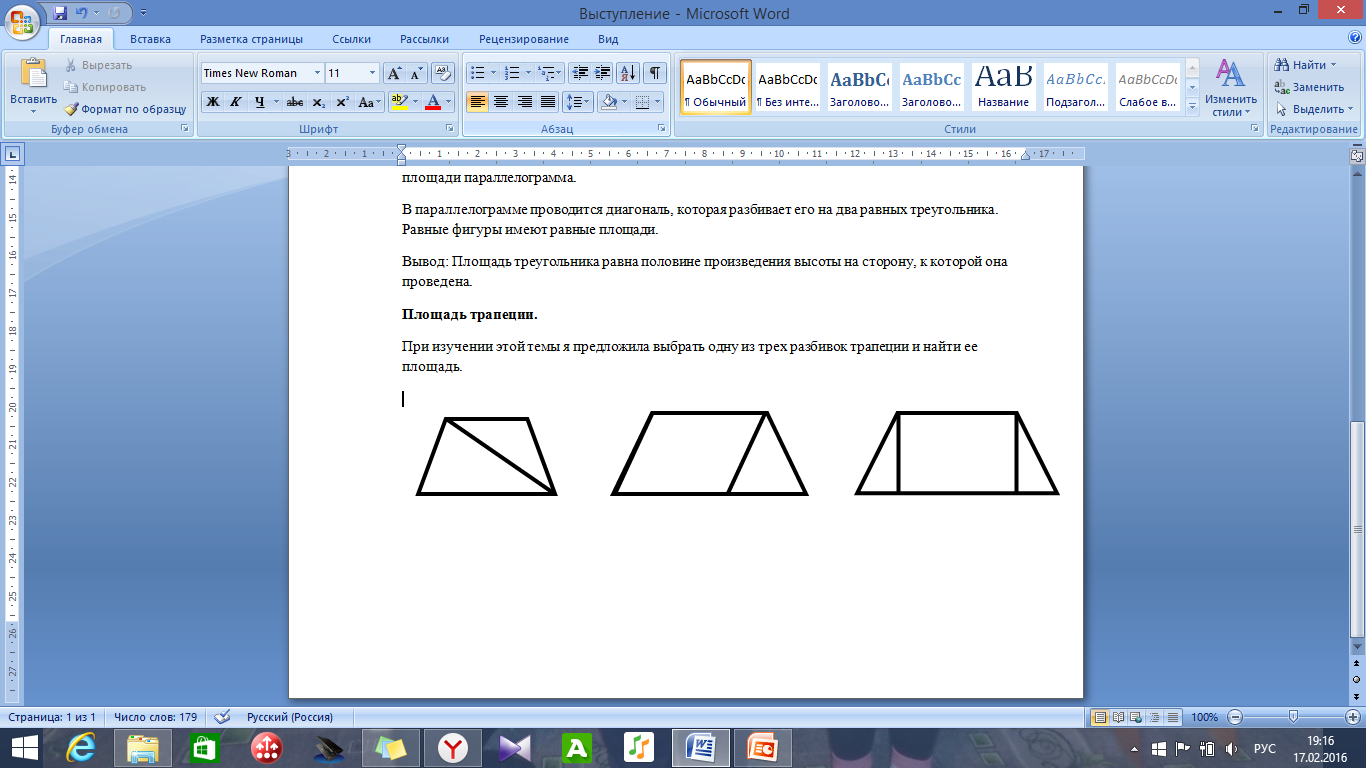
Ученики класса выбрали второй случай, но соединили еще две точки В и М. В итоге получили три треугольника. Составили формулу нахождения площади сложной фигуры и расписали ее по нашим обозначениям. Затем исходили из определения трапеции: в трапеции две стороны параллельны. А перпендикуляры, проведенные к параллельным прямым, равны. Поэтому, выполнив некоторые преобразования, мы получили, что площадь трапеции равна половине произведения суммы оснований на высоту, проведенную к основаниям.
Площадь ромба.
В ромбе провели одну из диагоналей, и нашли площади двух получившихся, равных треугольников. Но сумма высот треугольников является высотой ромба. Отсюда получили формулу нахождения площади ромба через его диагонали.
</ После изучения этого раздела, я совместно с учителями составила вспомогательный кластер по этой теме.