- Учителю
- Задачи на оптимизацию
Задачи на оптимизацию
Открытый урок - семинар по теме «Задачи на оптимизацию» (10 -11 класс)
Цель: Показать связь математики с реальной действительностью; формировать умение наблюдать, обобщать, проводить рассуждения по аналогии; развивать мышление и речь учащихся.
Сформировать умение применять алгебраический аппарат к изучению реальной действительности.
За неделю до проведения урока - семинара класс делиться на 5 - 6 групп, каждая из которых получает индивидуальное задание. Все учащиеся группы решают 2 - 3 задачи, а один из них готовит сообщение или решение одной данной задачи для остальных учащихся класса.
Ход урока.
I. Исторический экскурс.
Урок начинается вступительными словами учителя.
Учитель: Человеку часто приходиться решать задачи оптимизации своей деятельности, в которых нужно с помощью наименьших затрат, сил, средств, материалов получить наилучший результат. Как из круглого бревна выпилить прямоугольную балку с наименьшим количеством отходов?
Каких размеров должен быть ящик при заданном расходе материала и чтобы его объем был наибольшим?
В каком месте следует построить мост через речку, чтобы дорога проходящая через него и соединяющая два города была кратчайшей?
А самая простая и самая древняя задача была такой: какой из всех прямоугольников заданного периметра имеет наибольшую площадь? Решена она была древнегреческим математиком Евклидом. Все задачи такого содержания в древней Греции были объединены одним названием - «задачи Дидоны». Они названы по имени легендарной основательницы одного из старейших городов Греции и его первой царицы Дидоны.
Согласно легенде, вынужденная бежать из своего родного города, Дидона вместе со своими спутниками прибыла на северный берег Африки и хотела приобрести у местных жителей землю для нового поселения. Ей согласились уступить участок земли, однако не больше, чем объемлет воловья шкура. Хитроумная Дидона разрезала воловью шкуру на узкие ремешки, и разложив их, сумела ограничить гораздо большую площадь по сравнению с той, которую можно было покрыть одной шкурой. Если учесть, что царица выбирала участок примыкающий к берегу моря, то математическую задачу, с которой она столкнулась, можно сформулировать так: какой формы должна быть кривая L, чтобы площадь фигуры, ограниченной этой кривой и заданной линией Г, была наибольшей?
Задача Дидоны очень сложная и относиться к специальному разделу высшей математики, так называемому вариационному исчислению. Ну, а мы с вами постараемся разобрать такие задачи, с которыми каждый из нас может встретиться. Сначала, мне бы хотелось, чтобы вы познакомились с одним законом, диктующим размеры и формы всех промышленных продуктов. Прослушаем о нем сообщение (сообщение Метелкиной Е.).
II. Что такое ГОСТы.
I группа: В технике все держится на стандартизации. Много в мире делается механизмов, и все они состоят из различных деталей. Со всех участков завода поступают готовые детали в сборочный цех, некоторые из них привозят из других городов, а также из разных стран. И все детали подходят друг к другу. Если бы это было не так, невозможно было бы собрать ни один прибор.
Соответствие деталей друг другу обеспечивает стандартизация - установление единых норм и требований, предъявляемых к сырью, полуфабрикатам, готовым изделиям и материалам. Службы стандартизации разрабатывают систему государственных (а часто и межгосударственных) стандартов - ГОСТов.
ГОСТ - это закон, диктующий размеры и формы всех промышленных продуктов. Стандартизуется все - детали машин, профили проката (балки, уголки, швеллеры, трубы), формы и размеры досок, кирпичей, бутылок и пакетов и многое, многое другое. [4]
Методы математики являются основой стандартизации, а значит и фундаментом всей промышленности.
Вспомним один старый анекдот.
Портной сказал заказчику, что на его костюм пойдет 4 метра, но потребовал принести 7 метров материи, объяснив необходимость в лишних метрах очень просто: «Остальное я искромсаю». Портной, очевидно, не собирался экономить материал заказчика, а в технике экономия материалов занимает важнейшее место. И следя за экономией, прежде всего ГОСТы. Они не допускают, чтобы заготовка, из которой делается деталь, намного превосходила размеры самой детали. Иначе ценные материалы - металл или дерево будут уходить в стружку в процессе вытачивания маленькой детали из слишком большой заготовки.
III. Решение задач по группам (методами дифференциального исчисления и графически).
Учитель: Решение многих задач практически приводит к отысканию наибольшего или наименьшего значений некоторой функции на некотором промежутке. Сейчас, каждая группа, имея свою задачу, над которой должны были подумать дома, попытается решить ее графически с помощью компьютера, а потом продемонстрирует всем остальным ее решение как графически, так и методом дифференциального исчисления (с помощью производной)
Итак, вам дается 7 минут, для того, чтобы решить и подготовиться к защите своих задач.
IV. Защита решений задач.
I группа:
Задача: Какова наибольшая площадь прямоугольного участка земли, который можно огородить куском проволоки длиной 2p?
Решение: Обозначим длину одной из сторон прямоугольника x, тогда длина другой стороны будет (p - x), а потому площадь участка ![]() . При этом
. При этом ![]() . Найдем критические точки функции S(x). Производная S(x) равна:
. Найдем критические точки функции S(x). Производная S(x) равна: ![]() . Она обращается в 0 при
. Она обращается в 0 при ![]() . Итак, надо найти наибольшее значение функции
. Итак, надо найти наибольшее значение функции ![]() при
при ![]() , p-x=p -
, p-x=p -![]() прямоугольник - квадрат со стороной
прямоугольник - квадрат со стороной ![]() и его площадь равна
и его площадь равна ![]() . Т.е. наибольшим значением площади прямоугольника будет площадь квадрата.
. Т.е. наибольшим значением площади прямоугольника будет площадь квадрата.
II группа:
Задача: из круглого бревна, толщина которого d см., следует вырезать балку прямоугольного сечения. Прочность балки пропорциональна ab2 (a, b - измерения сечения балки в см.). При каких значениях а и b прочность балки будет наибольшей?
Решение: Под толщиной круглого бревна понимается диаметр его более тонкого конца. Факторами на прочность балки являются диаметр бревна, форма и размеры сечения, вид древесины, из которой балка изготовлена (но этим условием мы пренебрегаем при решении задачи).
О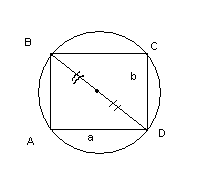
dбозначим прочность балки через Р, а коэффициент пропорциональности через k (k>0). По условию задачи Р=kab2. Тогда математическая задача может быть сформулирована следующим образом: «При каких значениях переменных а и b функция Р принимает наибольшее значение?
b2=d2 - a2 (AB=b, AD=a, BD=d) (рис.1).
Отсюда Р(а)=ka(d2-a2) a![]() (0;d).
(0;d). ![]()
![]() . Найдем критические точки функции:
. Найдем критические точки функции:![]() ,
, ![]() = 0
= 0 ![]()
![]() . или
. или ![]()
![]() (0;d) (рис.2).
(0;d) (рис.2).
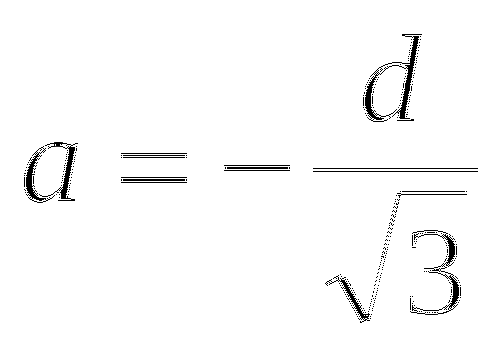

0 ![]() d
d
Рис.2.
При а![]() (0;
(0; ![]() ) Р'(a)>0 и, следовательно, функция Р(а) возрастает на (0;
) Р'(a)>0 и, следовательно, функция Р(а) возрастает на (0; ![]() ).
).
При а![]() (
(![]() ;d) Р'(a)<0 и, следовательно, функция Р(а) убывает на (
;d) Р'(a)<0 и, следовательно, функция Р(а) убывает на (![]() ;d).
;d).
Таким образом, точка ![]() - точка максимума и функция Р(а) принимает в ней наибольшее значение. (Если функция, непрерывная на промежутке, имеет на нем один экстремум, то он совпадает с ее наибольшим (наименьшем) значением на этом промежутке). Из равенства b2=d2- a2 имеем
- точка максимума и функция Р(а) принимает в ней наибольшее значение. (Если функция, непрерывная на промежутке, имеет на нем один экстремум, то он совпадает с ее наибольшим (наименьшем) значением на этом промежутке). Из равенства b2=d2- a2 имеем ![]() . Таким образом функция Р принимает наибольшее значение при
. Таким образом функция Р принимает наибольшее значение при ![]() и
и ![]() . Тогда прочность балки составляет
. Тогда прочность балки составляет ![]() .
.
Вывод: Уменьшение прочности балки при размерах прямоугольного сечения, отличных от оптимальных, означает, что балка либо не выдержит нагрузки, либо срок е службы будет меньше, а это экономически невыгодно.
Учитель
Отыскание наибольших и наименьших значений функции применяется при решении многих задач физики. Например, в положении равновесия потенциальная энергия системы достигает экстремального значения, причем в положении устойчивого равновесия потенциальная энергия максимальна. Рассмотрим еще следующий пример.
III группа. Задача: Найдем на АВ такую точку С, чтобы сумма длин отрезков МС и NC была минимальна.
М N
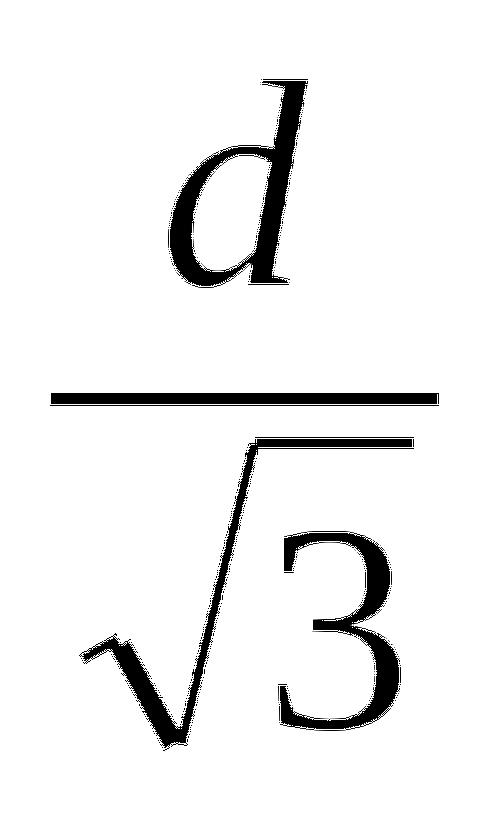

A x С l -x B
Рис.3.
Решение: Примем точку А за начало координат на прямой и обозначим координату точки С через х. (рис.3) МС=![]() и NC=
и NC=![]() , а потому f(x)=MC+NC=
, а потому f(x)=MC+NC=![]() +
+![]() .
.
Чтобы найти наименьшее значение функции f(x), вычислим ее производную и приравняем к нулю:
![]() . (1)
. (1)
Не решая полученного уравнения, заметим, что ![]() = sin
= sin![]() ,
, ![]() = sin
= sin![]() . Поэтому равенство (1) означает, что sin
. Поэтому равенство (1) означает, что sin![]() = sin
= sin![]() , откуда
, откуда ![]() =
=![]() (острые углы равны, если равны их синусы). Итак, сумма длин отрезков МС и NC будет наименьшей, если угол падения равен углу отражения. Из курса физики известно, что это равенство выполняется при отражении луча света. Значит, луч свет «выбирает» при отражении путь экстремальной длины.
(острые углы равны, если равны их синусы). Итак, сумма длин отрезков МС и NC будет наименьшей, если угол падения равен углу отражения. Из курса физики известно, что это равенство выполняется при отражении луча света. Значит, луч свет «выбирает» при отражении путь экстремальной длины.
Учитель: Ребята, в наше время всем нам приходиться много работать с компьютером. Я думаю, что всем нам будет интересна следующая задача
IV группа.:
Задача: На странице текст должен занимать 384 см2. Верхнее и нижнее поля должны быть по 3 см, левое и правое - по 2 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?
Решение: Пусть длина печатного текста будет хсм., причем ![]() , тогда ширина его -
, тогда ширина его - ![]() см.
см.
Р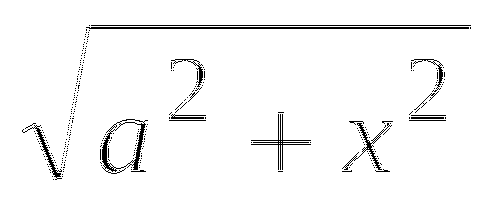 азмеры страницы соответственно будут (х+4)см и (
азмеры страницы соответственно будут (х+4)см и (![]() +6)см (рис.4).
+6)см (рис.4).
Площадь страницы S=(х+4)(![]() +6)=
+6)= ![]() .
.
Найдем производную S(x):
![]() ,
, ![]() при
при ![]() =0
=0 ![]() 6х2=1536
6х2=1536 ![]() х1 = 16 или х2 = - 16
х1 = 16 или х2 = - 16 ![]() (0;384).
(0;384).
Итак, размер листа должен быть 16+4=20 см, ![]() см.
см.
Ответ: 20 см. и 30 см.
Рис.4.
V группа:
З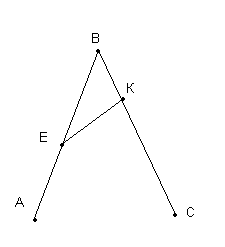 адача: Три пункта А, В, С не лежат на одной прямой, причем
адача: Три пункта А, В, С не лежат на одной прямой, причем ![]() АВС=600. Одновременно из точки А выходит автомобиль, а из точки В - поезд. Автомобиль движется по направлению к точке В со скоростью 80 км/ч, поезд - к точке С со скоростью 50 км/ч. В какой момент времени (от начала движения) расстояние между поездом и автомобилем будет наименьшим, если АВ=200 км?
АВС=600. Одновременно из точки А выходит автомобиль, а из точки В - поезд. Автомобиль движется по направлению к точке В со скоростью 80 км/ч, поезд - к точке С со скоростью 50 км/ч. В какой момент времени (от начала движения) расстояние между поездом и автомобилем будет наименьшим, если АВ=200 км?
Р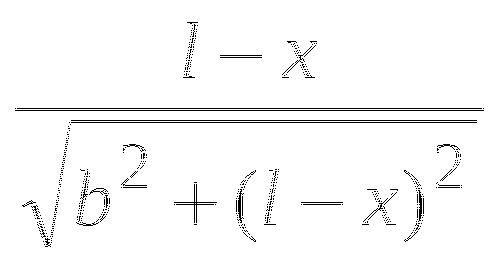 ешение: Пусть в момент времени t, t
ешение: Пусть в момент времени t, t ![]() [0;
[0;![]() ], т.е t
], т.е t ![]() [0;2,5], автомобиль находится в точке Е, а поезд в точке К. Тогда ВЕ=200-80t, ВК=50t. По теореме косинусов: ЕК2 = ВК2+ ВЕ2 - 2 ВЕ ВКcos В.
[0;2,5], автомобиль находится в точке Е, а поезд в точке К. Тогда ВЕ=200-80t, ВК=50t. По теореме косинусов: ЕК2 = ВК2+ ВЕ2 - 2 ВЕ ВКcos В.
ЕК2 =(200 - 80t)2+(50t)2 - 2*![]() *50(200 - 80t)t =12900 t2-42000 t+40000. Пусть ЕК2= S(t)= 12900 t2-42000 t+40000.
*50(200 - 80t)t =12900 t2-42000 t+40000. Пусть ЕК2= S(t)= 12900 t2-42000 t+40000.
S' (t)=25800t-42000 S' (t)=0 ![]() 25800 t=42000
25800 t=42000 ![]() t=
t=![]()
![]() [0;2,5], поэтому наименьшее значение ЕК2 достигается при t=
[0;2,5], поэтому наименьшее значение ЕК2 достигается при t=![]() = 1
= 1![]() (часа)
(часа)
Учитель: Подводя итог решению всех рассмотренных задач с помощью дифференциального исчисления, заметим, что все задачи решаются по следующему плану:
-
Выбирают одну из переменных (независимую переменную) и выражают через нее ту переменную, для которой ищется наибольшее или наименьшее значение.
-
Находят промежуток изменения независимой переменной.
-
Находят производную полученной в пункте 1 функции.
-
Находят критические точки функции ( в том числе и те, в которых производная не существует).
-
Определяют какие из них принадлежат промежутку из пункта 2.
-
Находят наибольшее или наименьшее значение функции.
При этом для простоты вычислений полезно иметь в виду следующие замечания:
-
Точка, в которой функция принимает наибольшее или наименьшее значение, не изменяется при следующих преобразованиях выражения задающего функцию:
а) прибавление постоянного слагаемого;
б) умножение на отличное от нуля число (только при умножении на отрицательное число наибольшее значение переходит в наименьшее и обратно);
в) возведение в степень с натуральным показателем, если функция неотрицательна.
Например, функция ![]() имеет на отрезке [0;7] наибольшее значение в той же точке, что и функция
имеет на отрезке [0;7] наибольшее значение в той же точке, что и функция ![]() .
.
2) Если положительная функция f принимает в точке а наибольшее (наименьшее) значение, то функции -f и ![]() принимают в той же точке наименьшее (соответственно наибольшее) значение.
принимают в той же точке наименьшее (соответственно наибольшее) значение.
Например, функция (х-2)2+5 принимает наименьшее значение при х=2, а потому функция ![]() имеет при х=2 наибольшее значение.
имеет при х=2 наибольшее значение.
На этом уроке мы ограничились рассмотрением алгебраических задач, но и геометрические задачи тоже сводятся к алгебраическим.
Одним из сильных методов решения геометрических задач на экстремумы функции является использование неравенств, в частности, неравенства о среднем арифметическом и среднем геометрическом (неравенства Коши):
![]() , т.е.
, т.е. ![]() или, в общем виде:
или, в общем виде: ![]() .
.
Решим задачу:
Каких размеров должен быть ящик, чтобы при заданной площади поверхности S, его объем был наибольшим?
Решение:
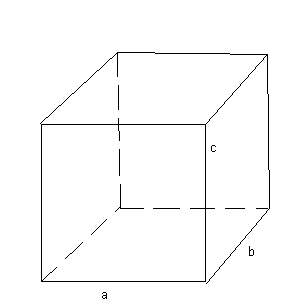
S пов =2(ab+bc+ac), V=abc, ab+bc+ac=![]()
![]()
![]()
![]()
![]()
ab=bc=ac ![]() a=b=c
a=b=c
Итак, среди всех ящиков с заданной площадью полной поверхности наибольший объем имеет ящик кубической формы.
V. Итог урока.
Мы сегодня показали, как важны знания математики человеку, сидящему за компьютером, строителю, инженеру, экономисту, а так же простому плотнику; показали связь математики с другими предметами, в частности, с физикой и информатикой. Надеюсь, что эти знания пригодятся в жизни.
Список используемой литературы.
-
Виленкин Н.Я. «Алгебра и математический анализ».Учебное пособие для учащихся школ и классов с углубленным изучением математики.
-
Колмагоров А.Н. «Алгебра и начала анализа». Учебник для 10 - 11 классов общеобразовательных учреждений.
-
Журнал «Математика в школе» №7, 2003 г.
-
Детская энциклопедия», т.5, АПН РСФСР, 1960 г.
7