Семинары по математике Иррациональные уравнения и неравенства

Семинар:

Автор-составитель:

Воробьева Инна Викторовна

Предмет: Алгебра и начала анализа

Классы: 10А, 11А.

Тема: «Иррациональные уравнения»

1-ый семинар для учащихся 10-11 классов

Свойства корней

1. Основное свойство корня:

.

2. Умножение корней:

, a, b .

3. Деление корней:

a, b .

4. Возведение корня в степень:

, .

5. Извлечение корня из корня:

, a.

6. Вынесение множителя из-под знака корня:

, b, в частности:

,

.

7. Внесение множителя под знак корня:

.

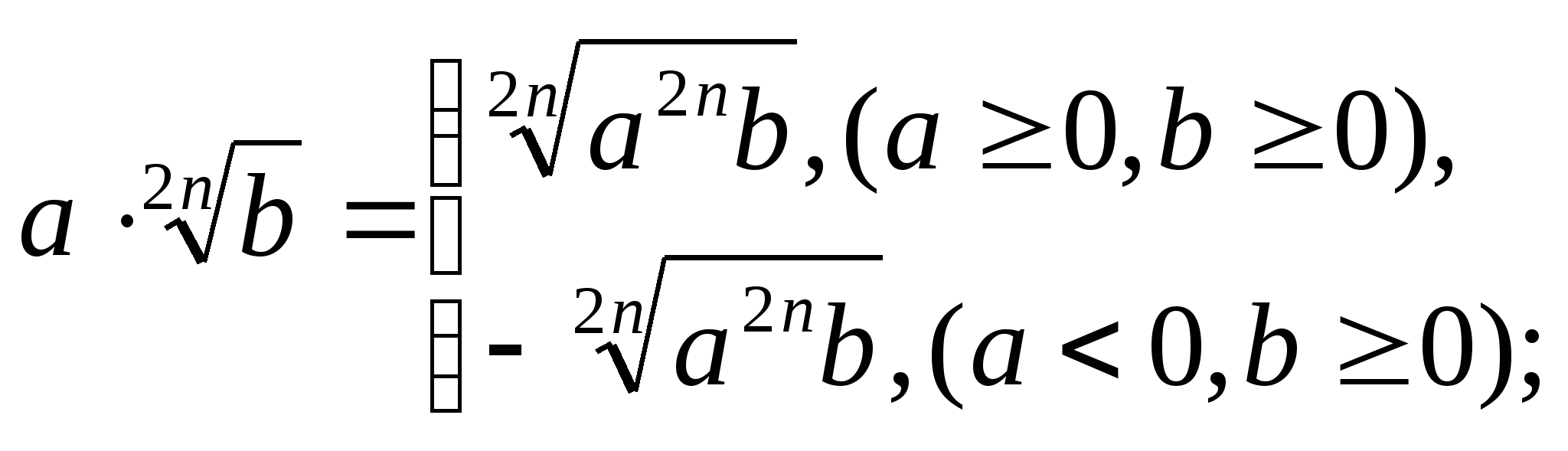
Определение. Уравнения, в которых под знаком корня содержится переменная, называют иррациональными.

При решении иррациональных уравнений необходимо учитывать следующее:

1. Если показатель радикала - четное число, то подкоренное выражение должно быть неотрицательным;

2. Если показатель радикала - нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак радикала совпадает со знаком подкоренного выражения.

Методы решения иррациональных уравнений, как правило, основаны на возможности замены с помощью некоторых преобразований иррационального уравнения рациональным уравнением, которое либо равносильно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного уравнения.

I группа. .

Если а<0, то уравнение не имеет корней.

Если а0, то f(x)=a.

Примеры:

a) - решения нет.

б) .

Ответ: 2.

II группа. . или .

Из 2-х систем выбираем ту, которая решается легче.

Пример:

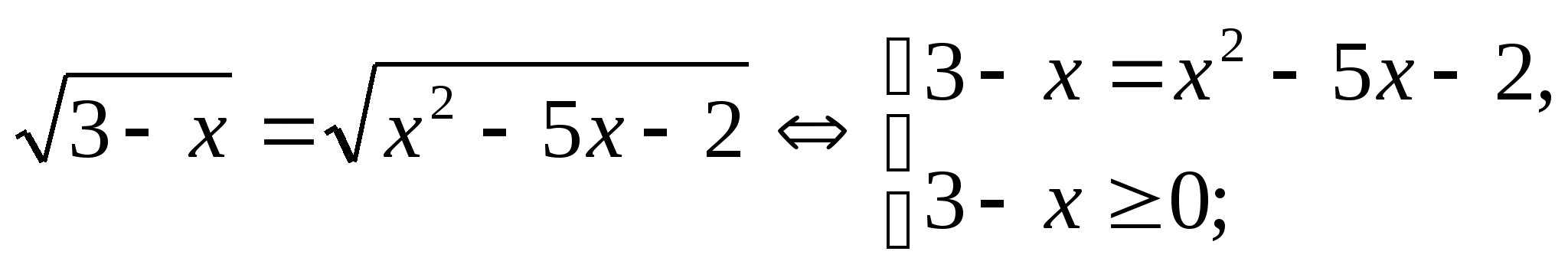
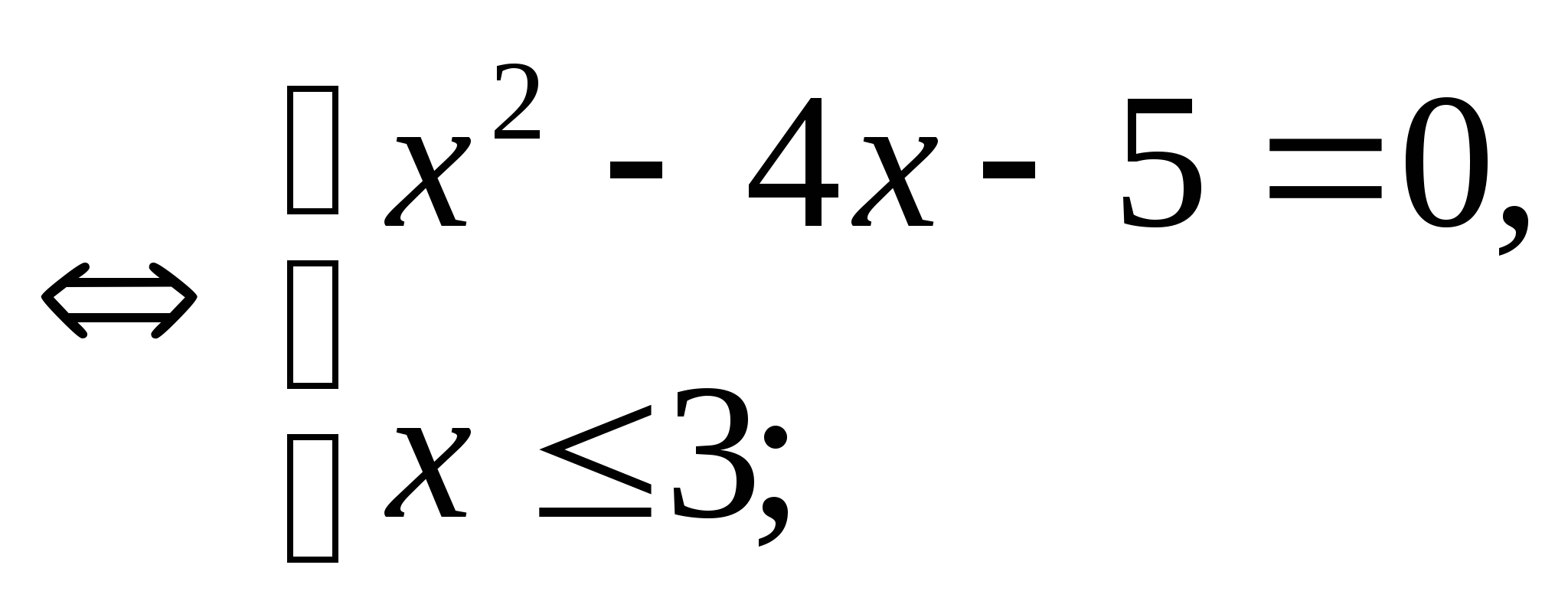
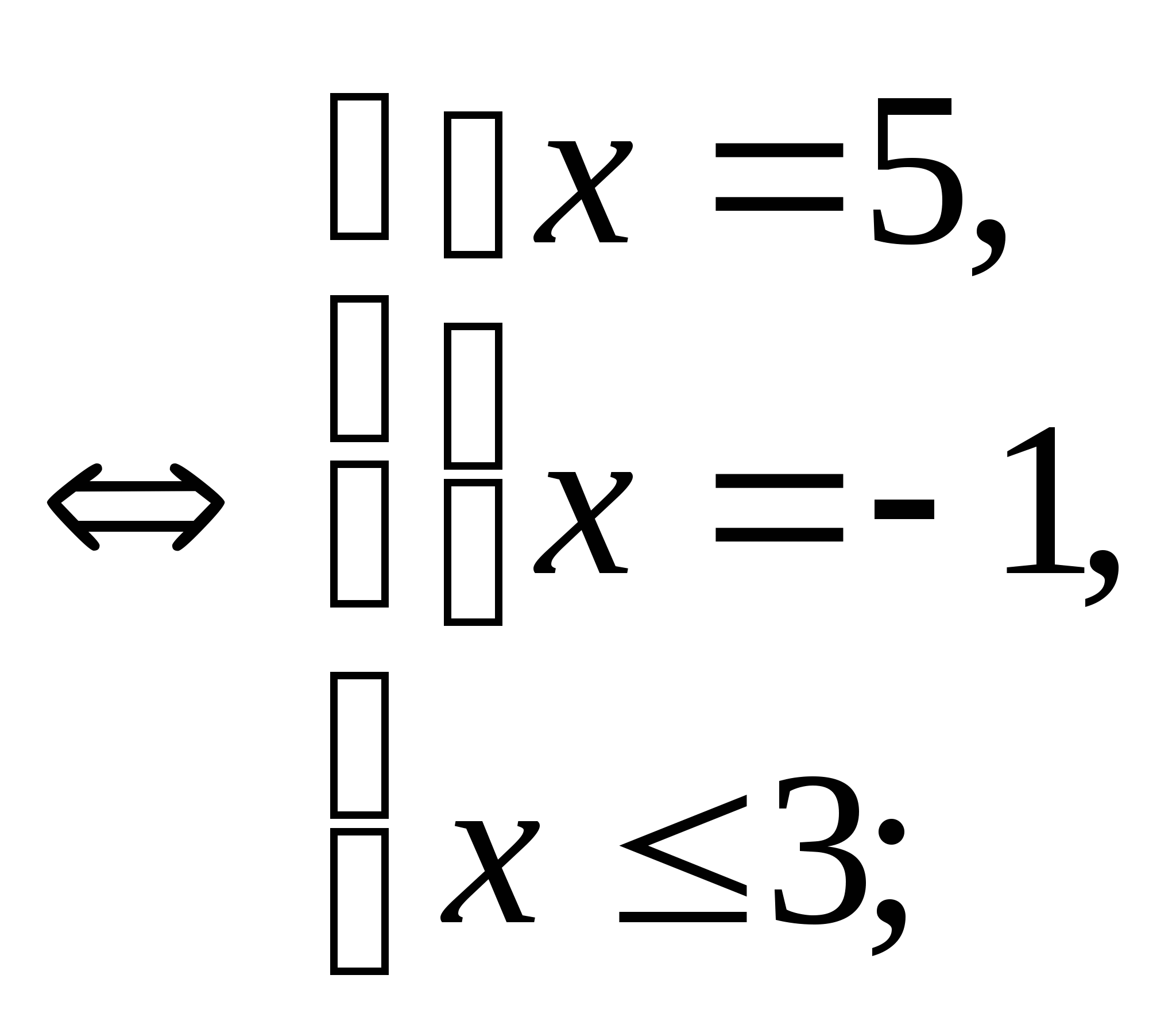
Ответ: -1..

III группа. .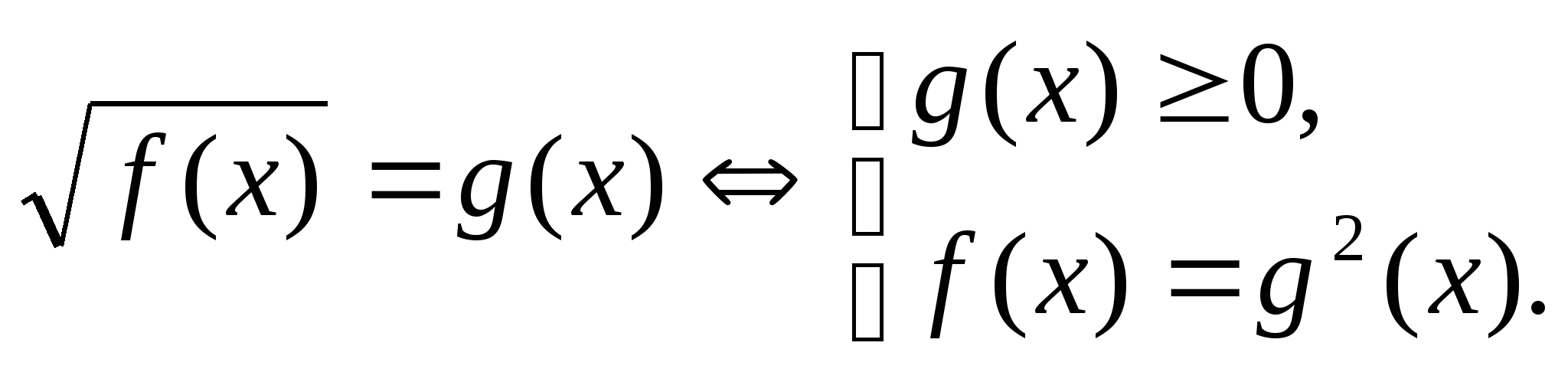

Пример:

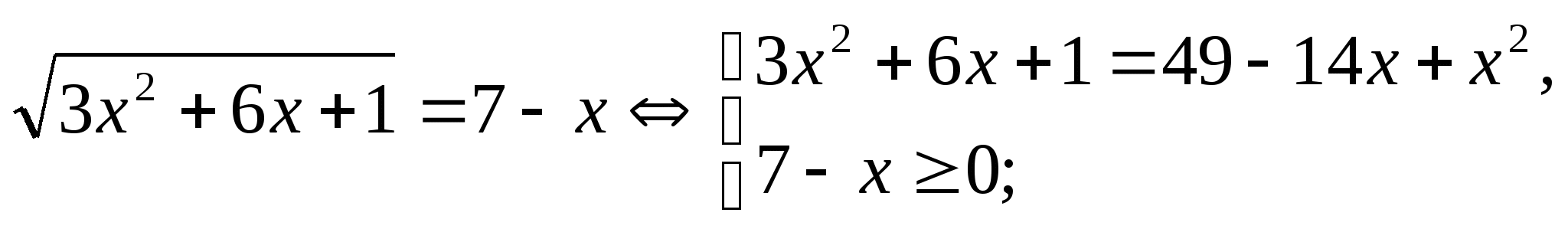
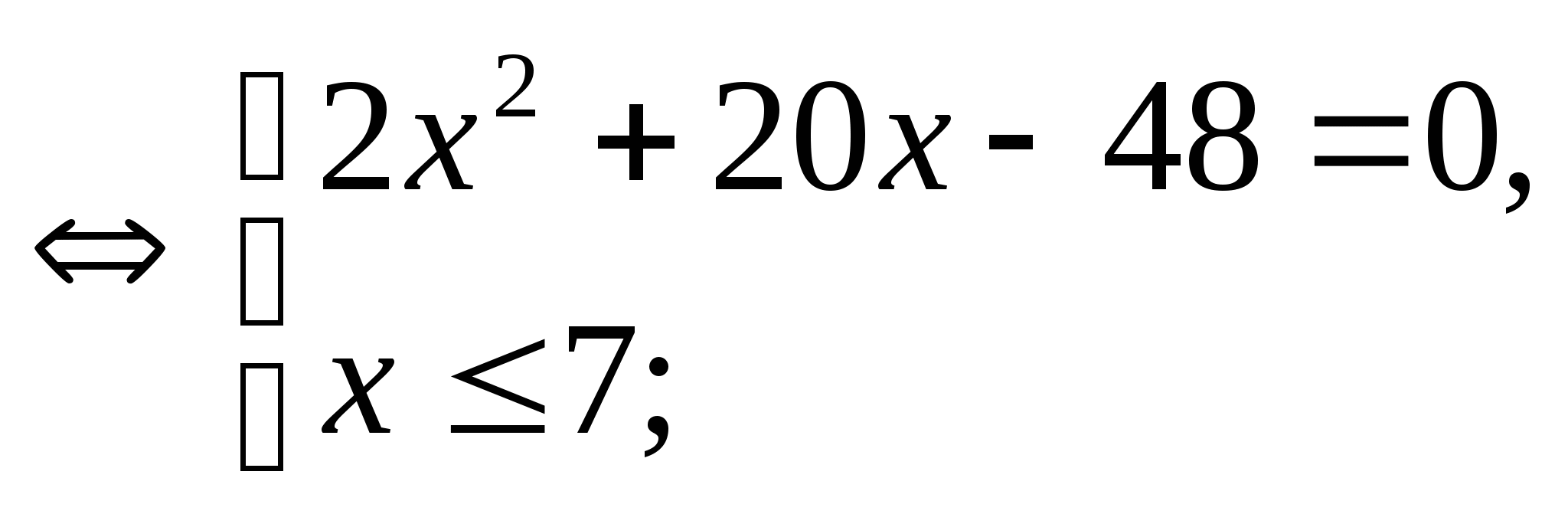
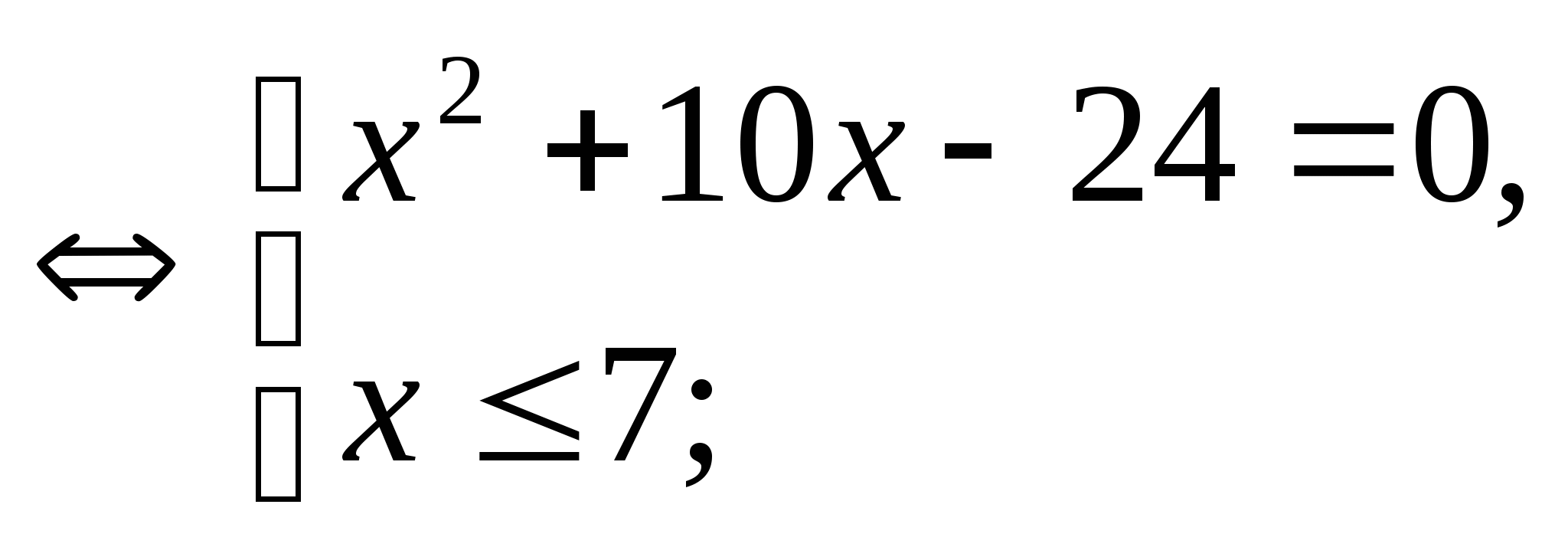
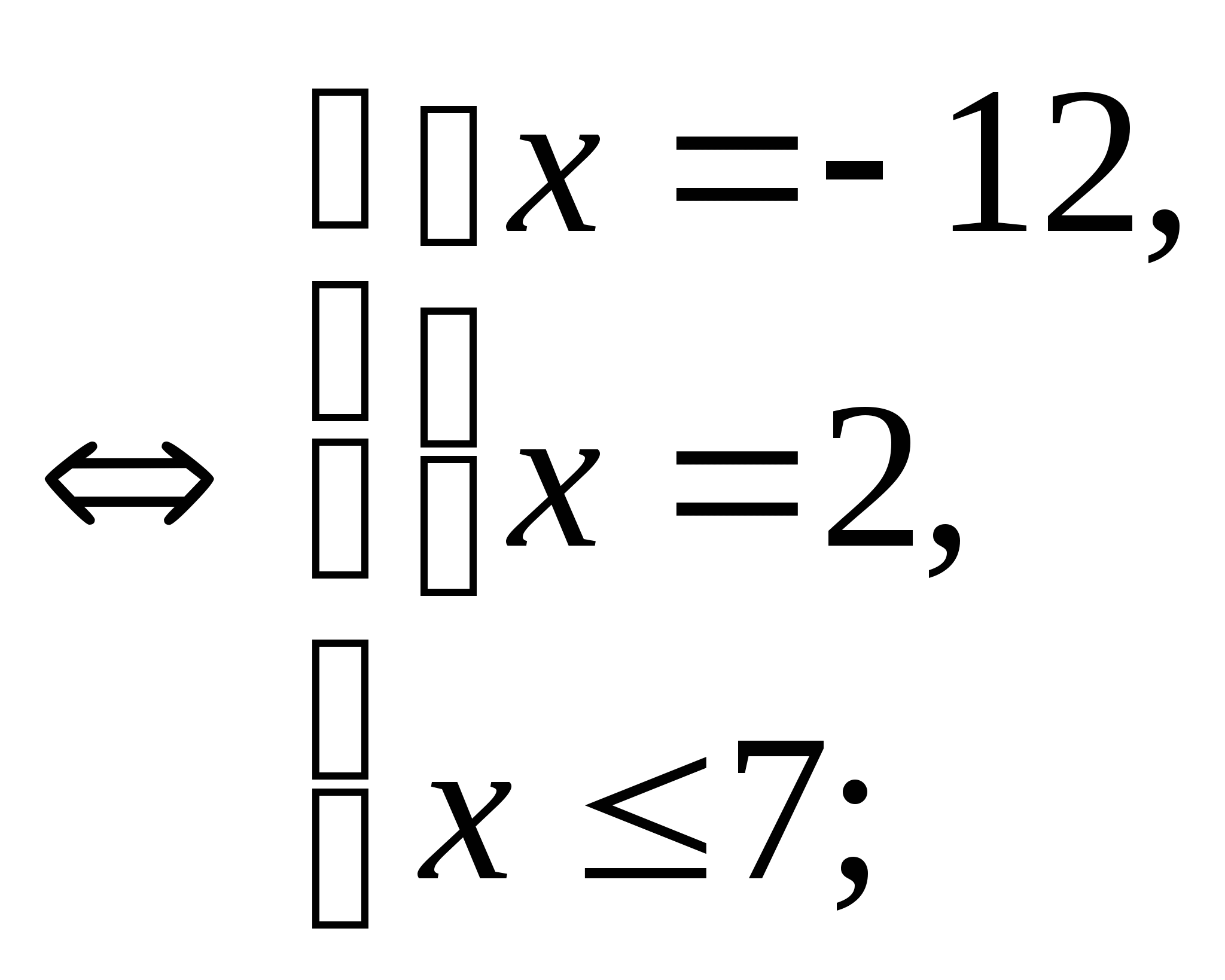
Ответ: -12;2.

IV группа. Уравнения, для которых нахождение области определения обязательно.

Примеры:

a) .

ОДЗ: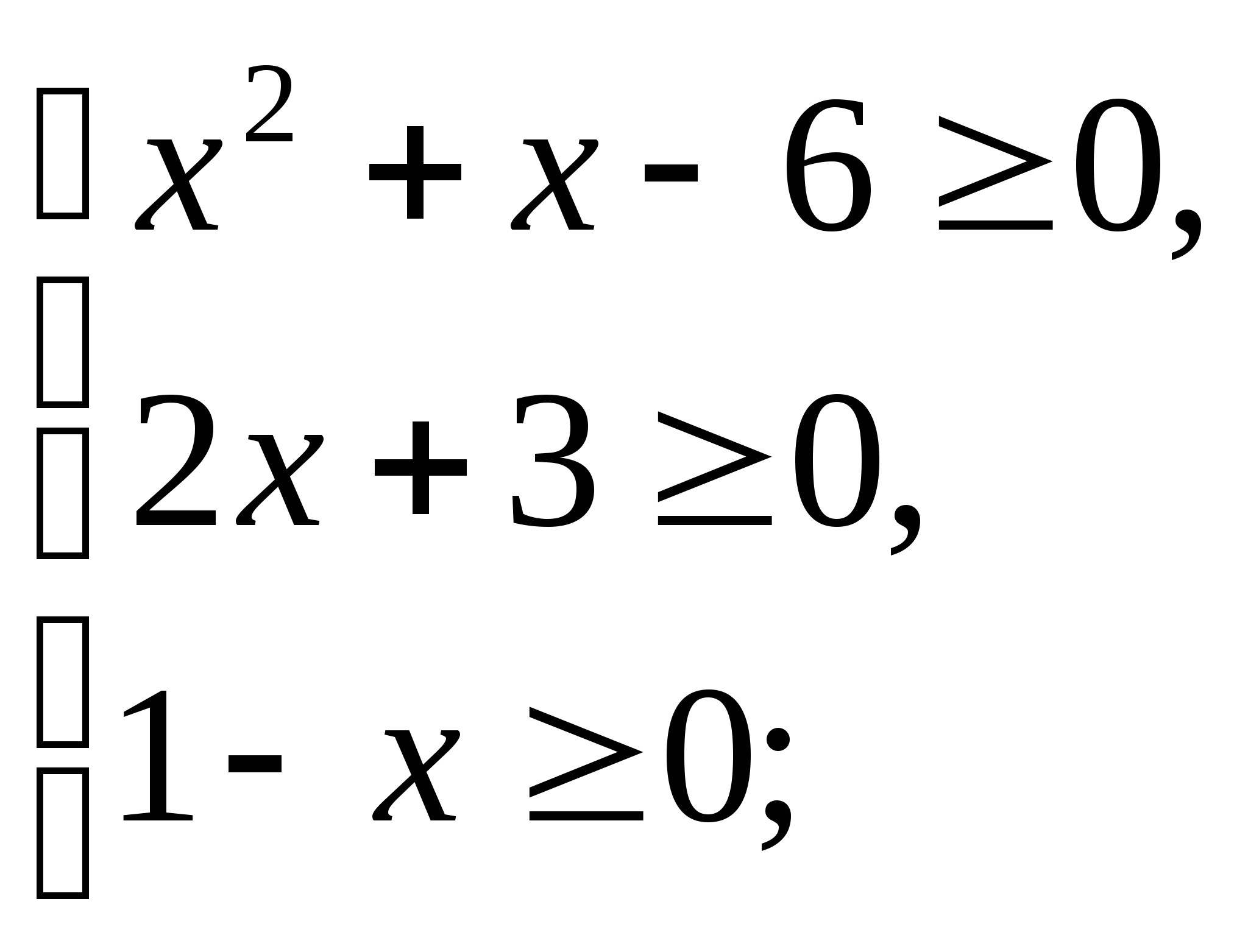

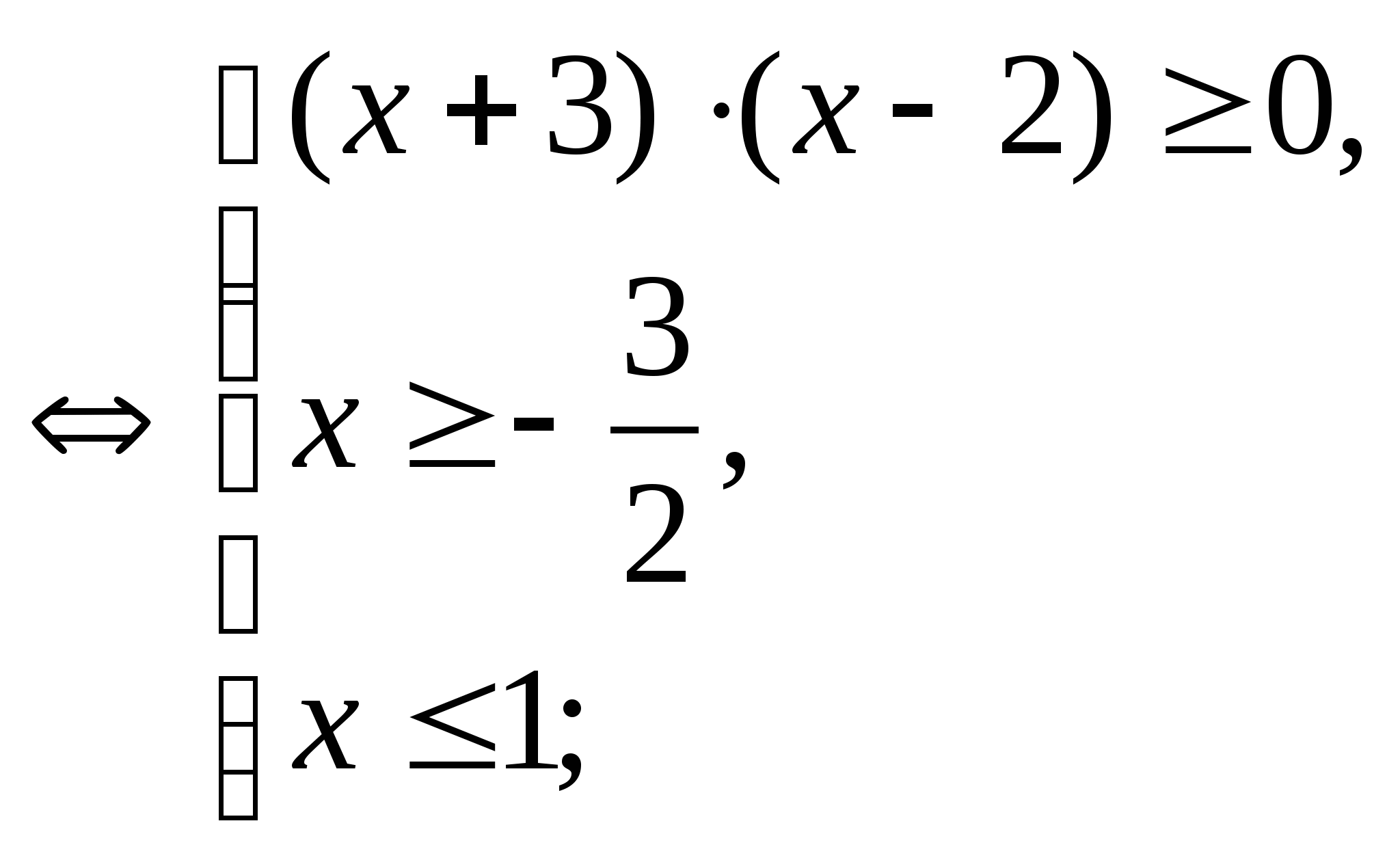
Ответ:.

б) .

3+x² всегда > 0. Значит, для данного уравгнгия:

.

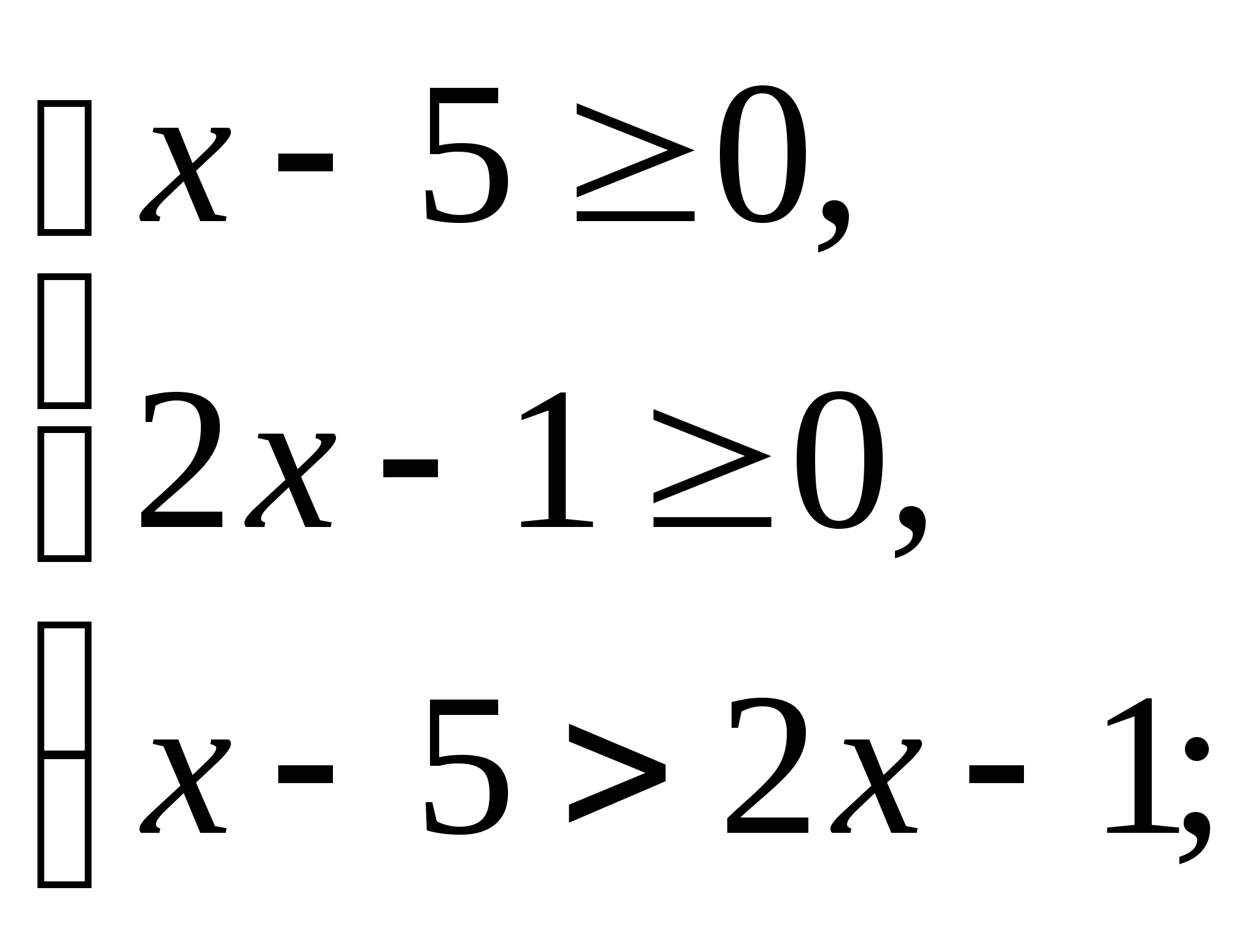
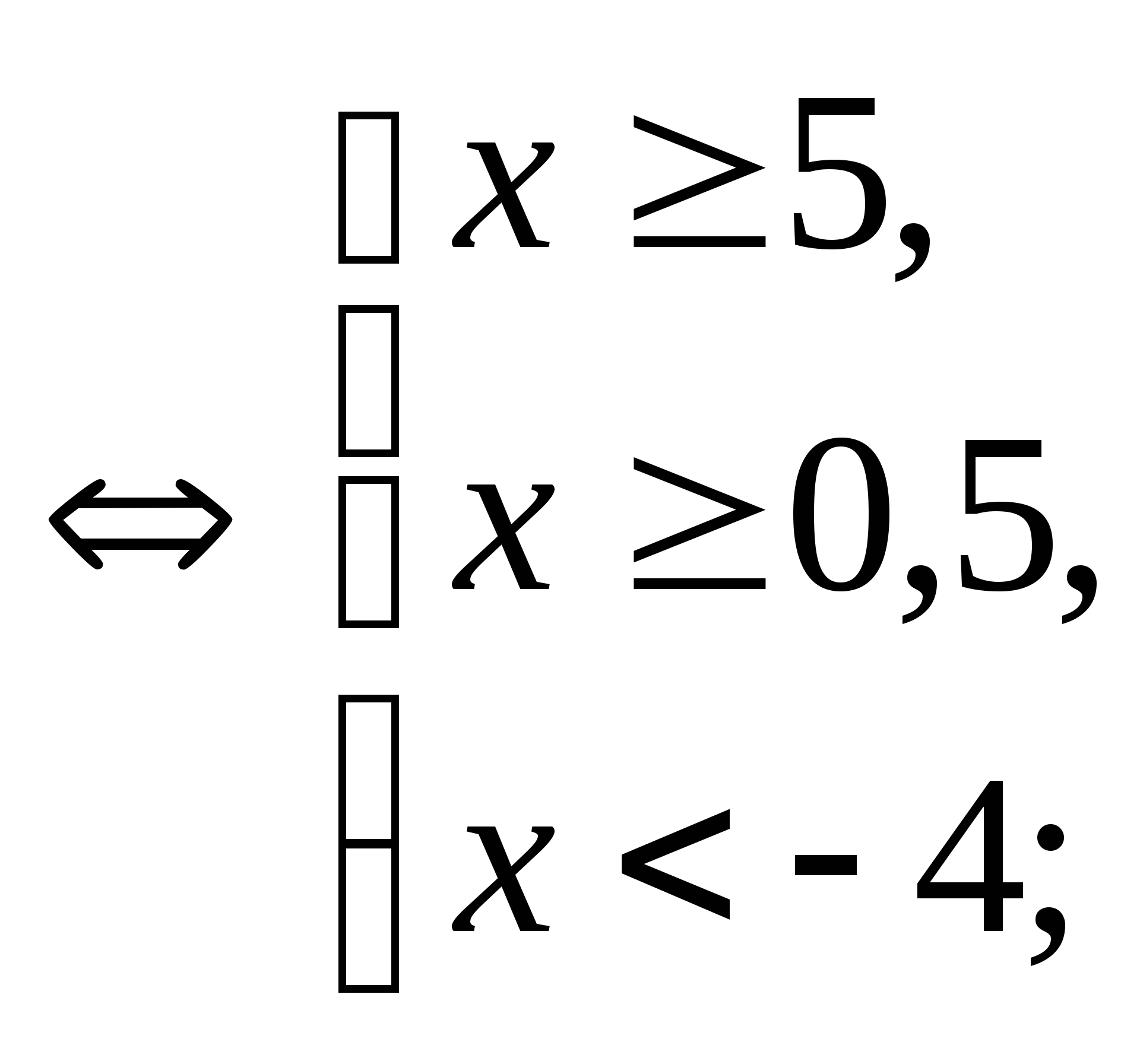
Ответ:.

в) .

ОДЗ:

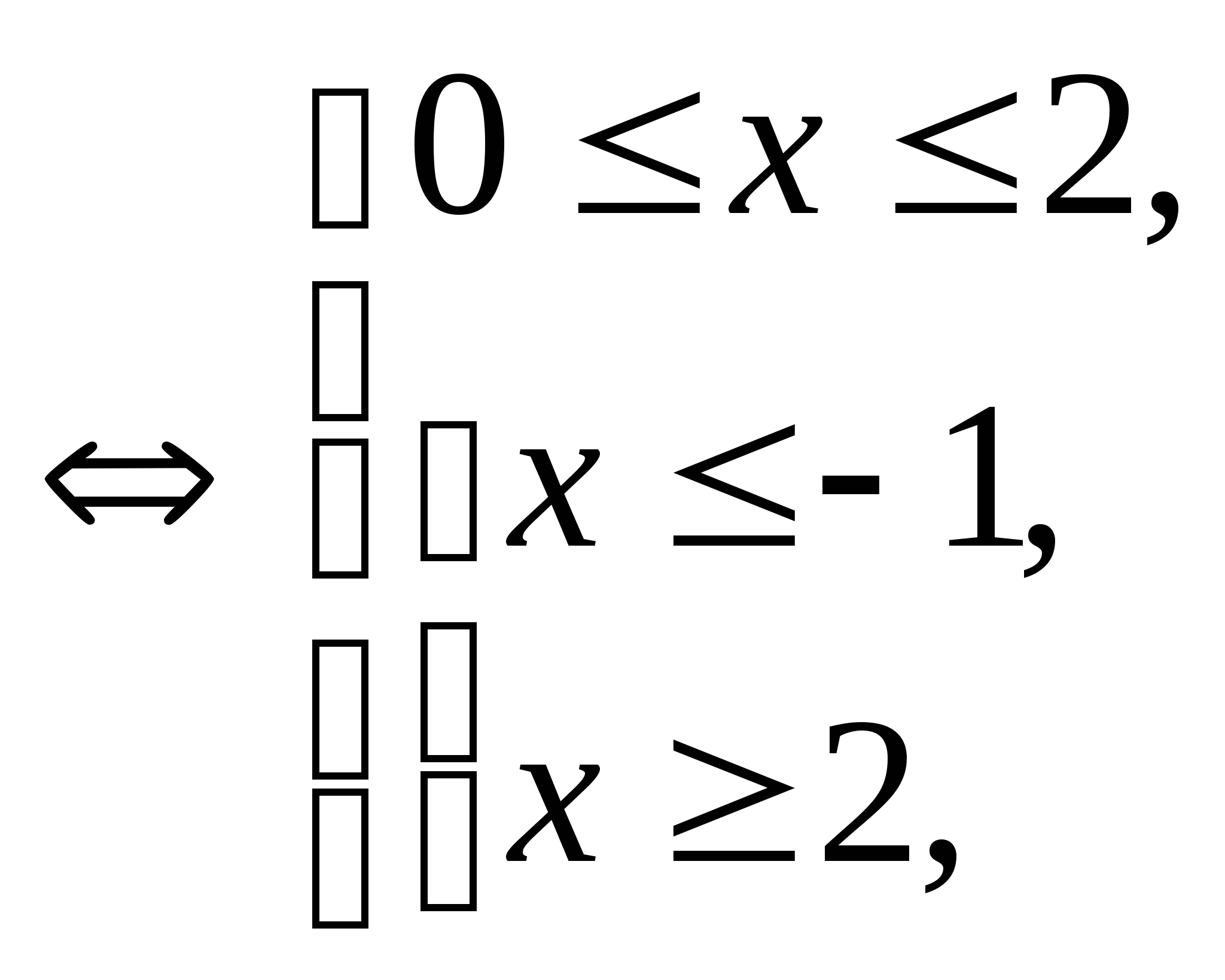
Проверка:

Ответ: 2.

V группа. Уравнения, которые решать не надо.

Примеры:

a) - решения нет.

б) - решения нет.

в) - решения нет.

VI группа. Разные уравнения.

Примеры:

a) .

ОДЗ: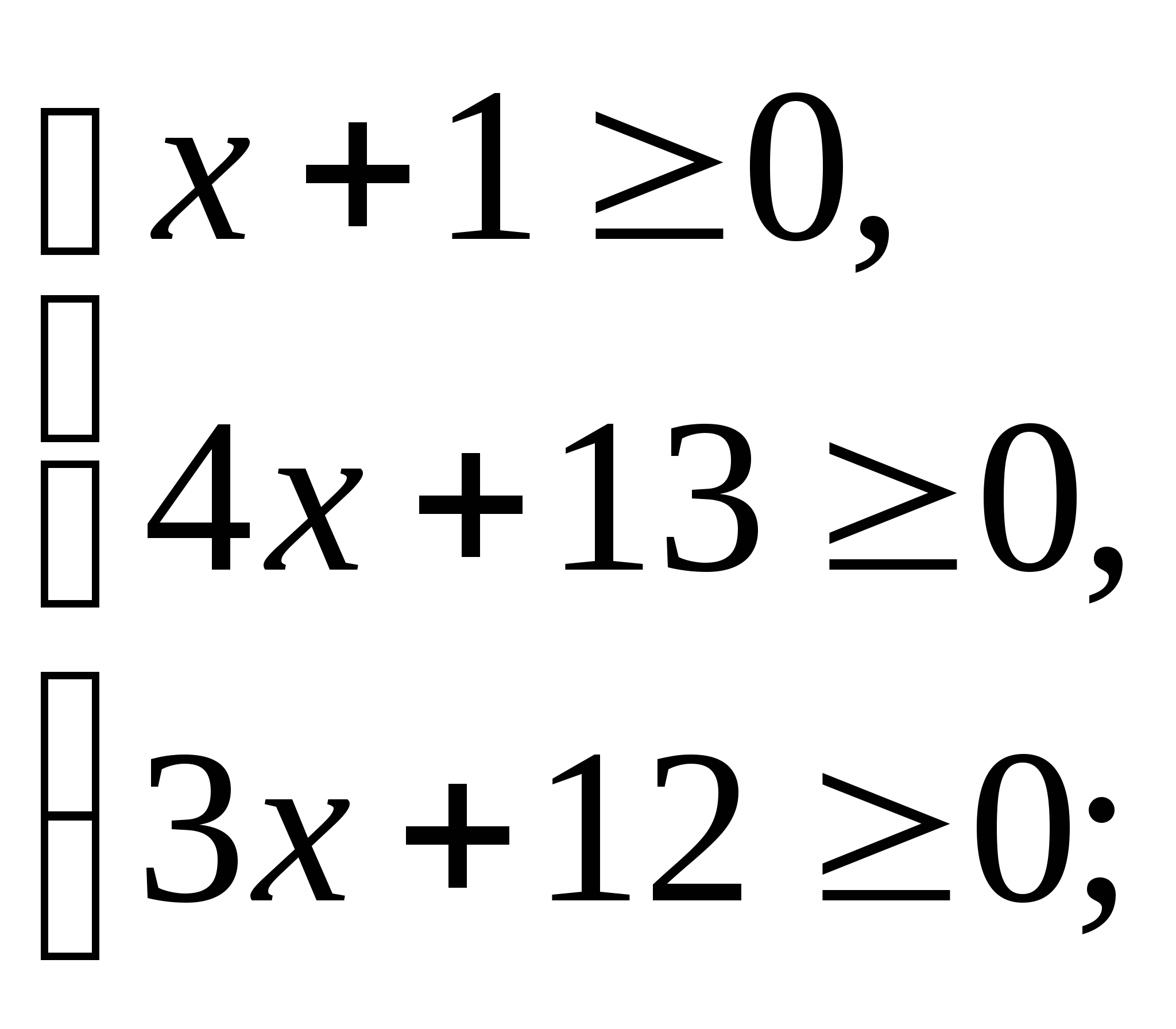

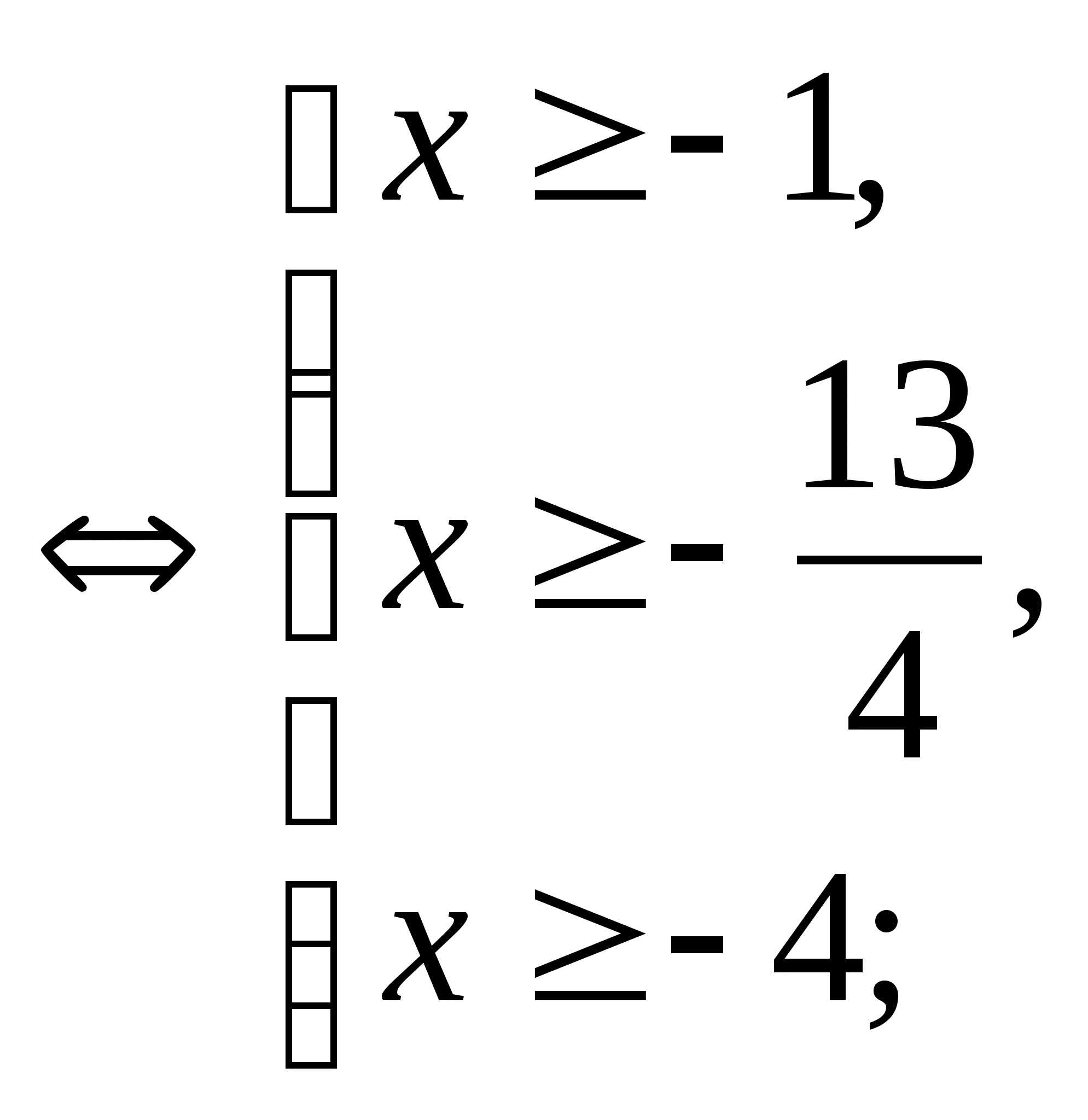
Запишем уравнение в виде:

, возведем в квадрат:

x=-1 или x=-4,

x=-4 - посторонний корень, т.к. не входит в ОДЗ.

Проверка: , 3=3.

Ответ: -1.

б) .

ОДЗ: x+2.

, возведем в 6 степень.

(x+2)³=(3x+2)²,

x³+6x²+12x+8=9x²+12x+4,

x³-3x²+4=0,

x³-3x²+1+3=0, (x³+1)-3(x²-1)=0, (x+1)(x²-x+1)-3(x+1)(x-1)=0,

(x+1)(x²-x+1-3x+3)=0,

(x+1)(x²-4x+4)=0,

(x+1)(x-2)²=0,

x=-1 или x=2.

Оба корня входят в ОДЗ.

Проверка:

- неверно, x=-1 - посторонний корень.

- верно.

Ответ: 2.

в) .

ОДЗ: .

,

,

Пусть ,

,

8y²+8-65y=0,

8y²-65y+8=0,

,

;

, или .

, ,

, ,

, ,

, ,

, .

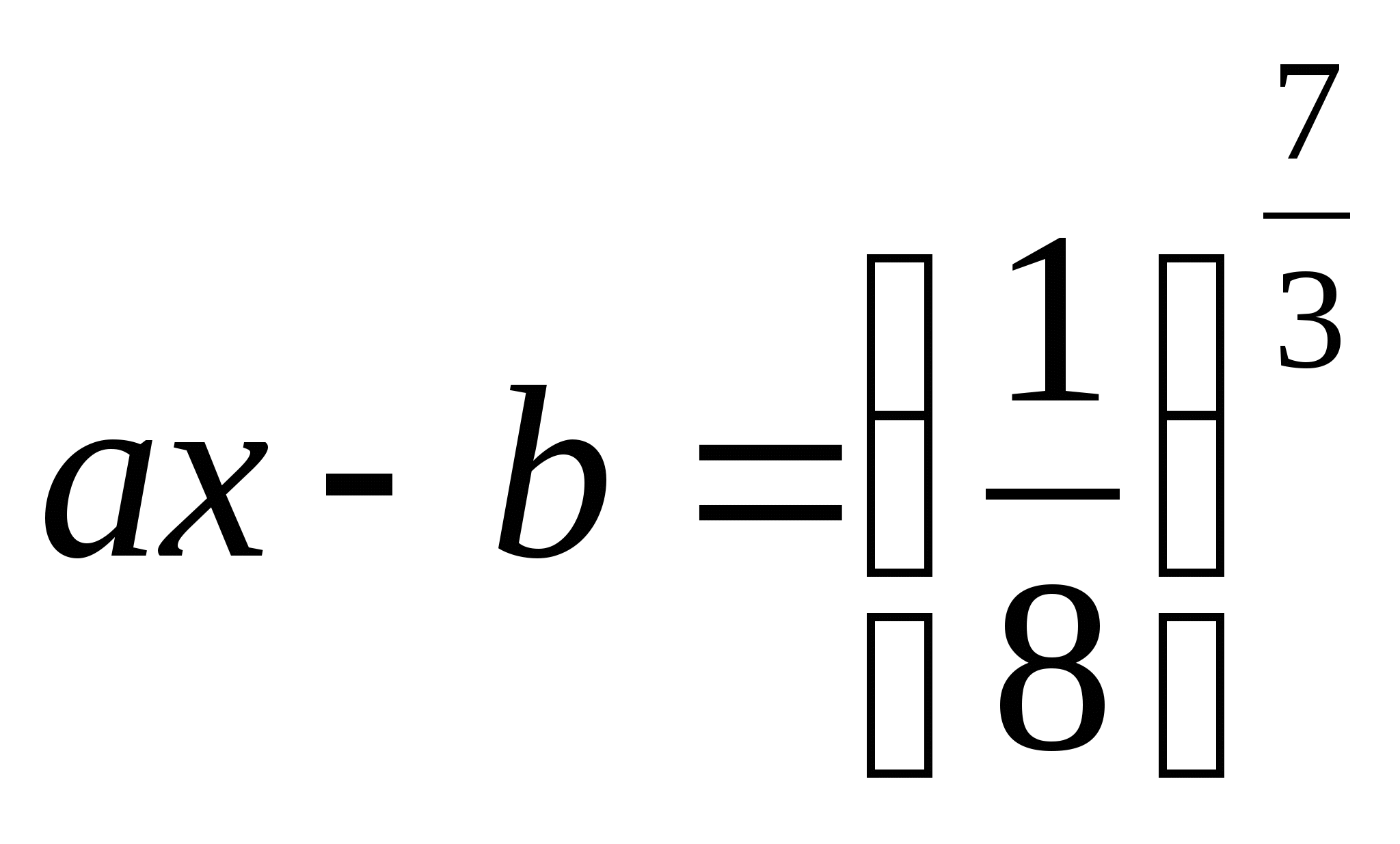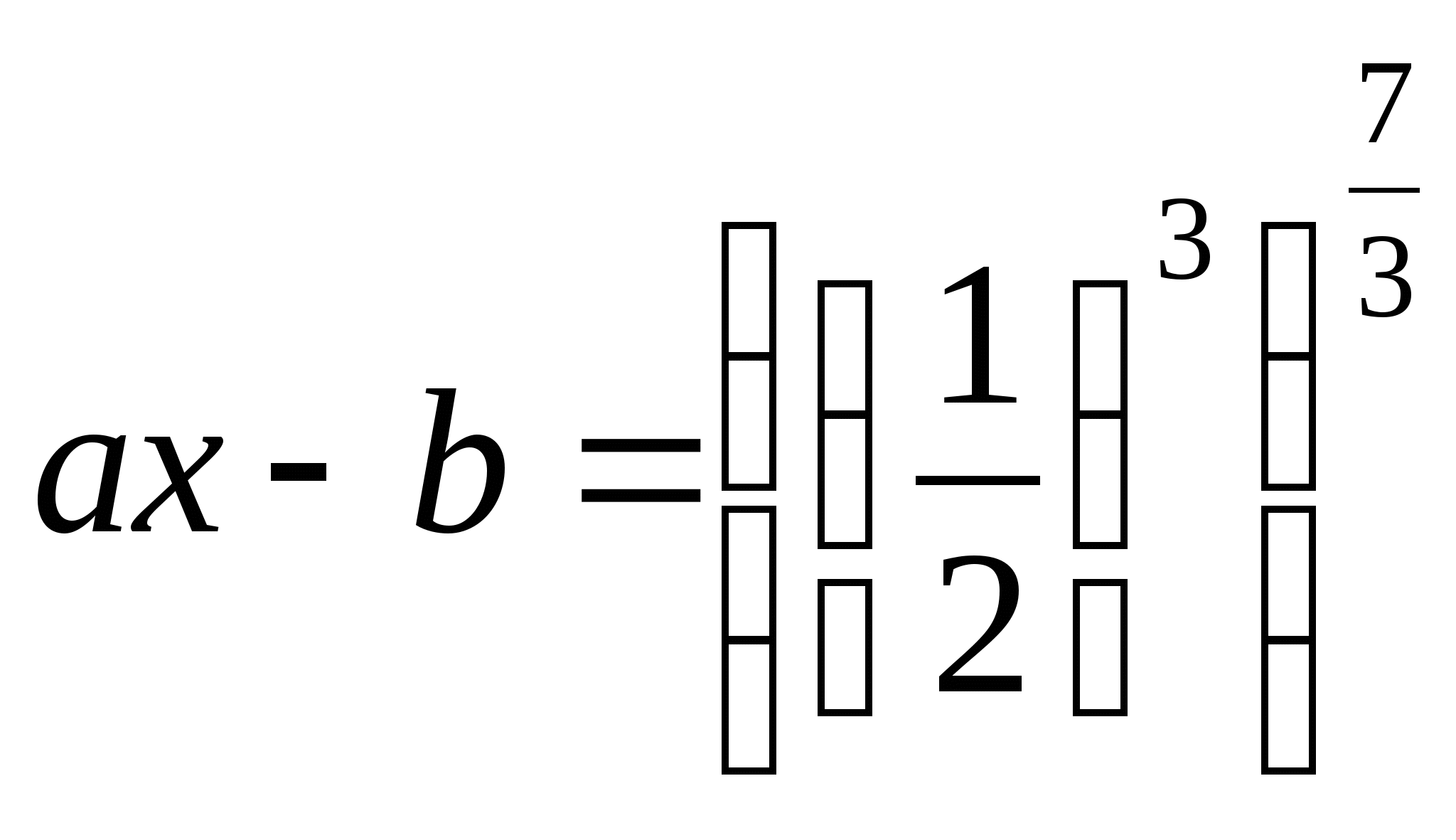Ответ: ; .

г) .

ОДЗ: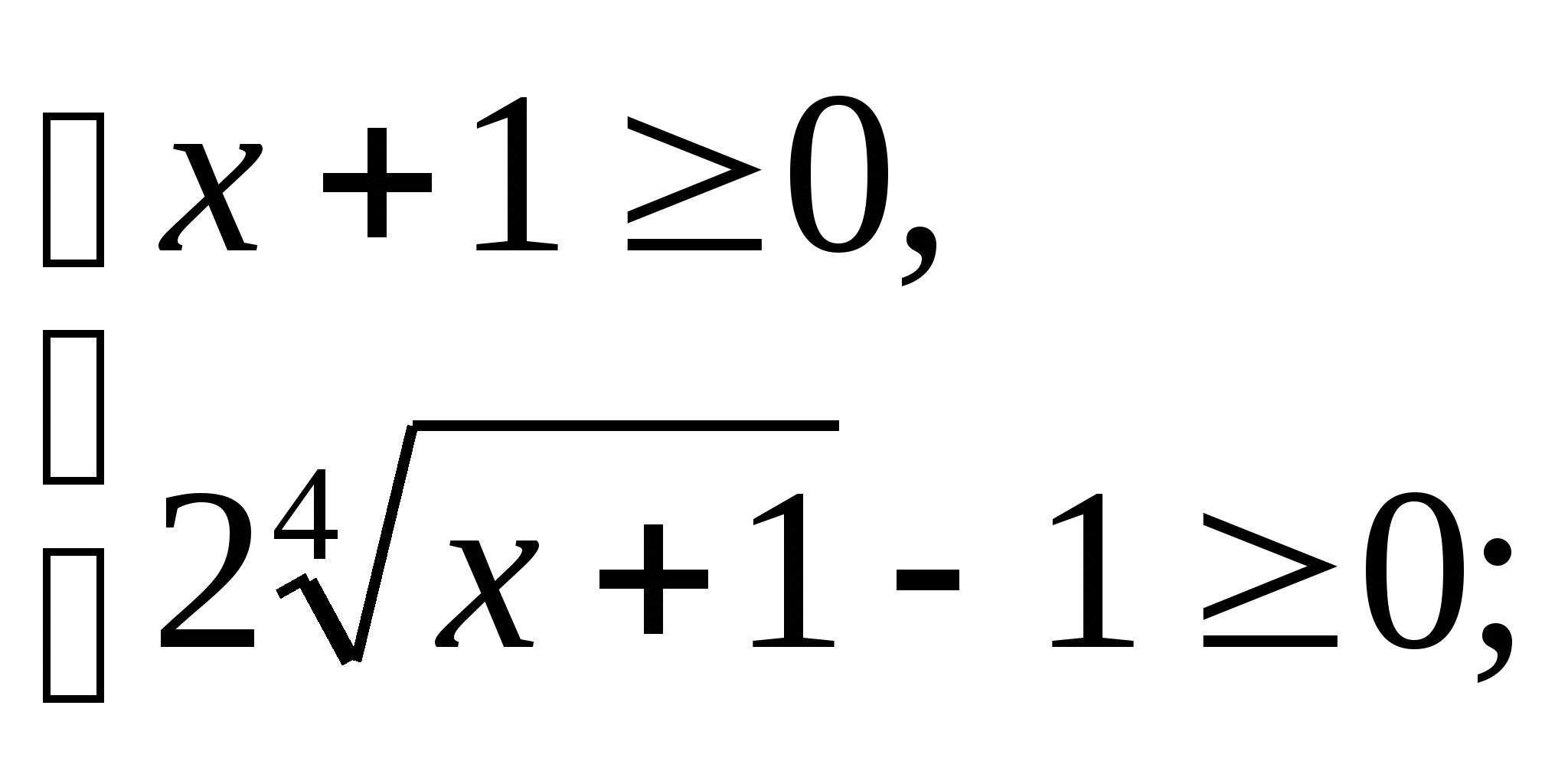

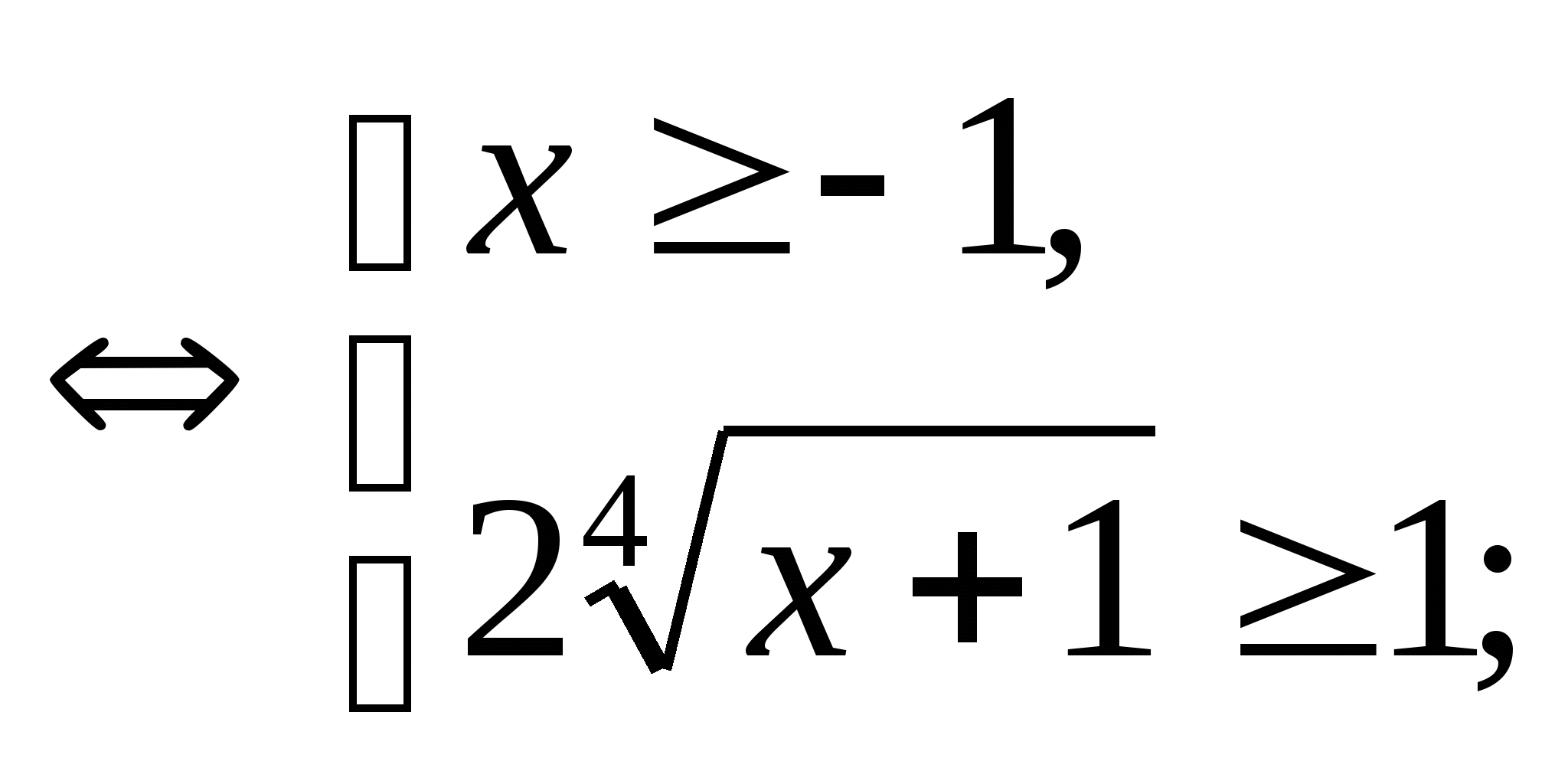
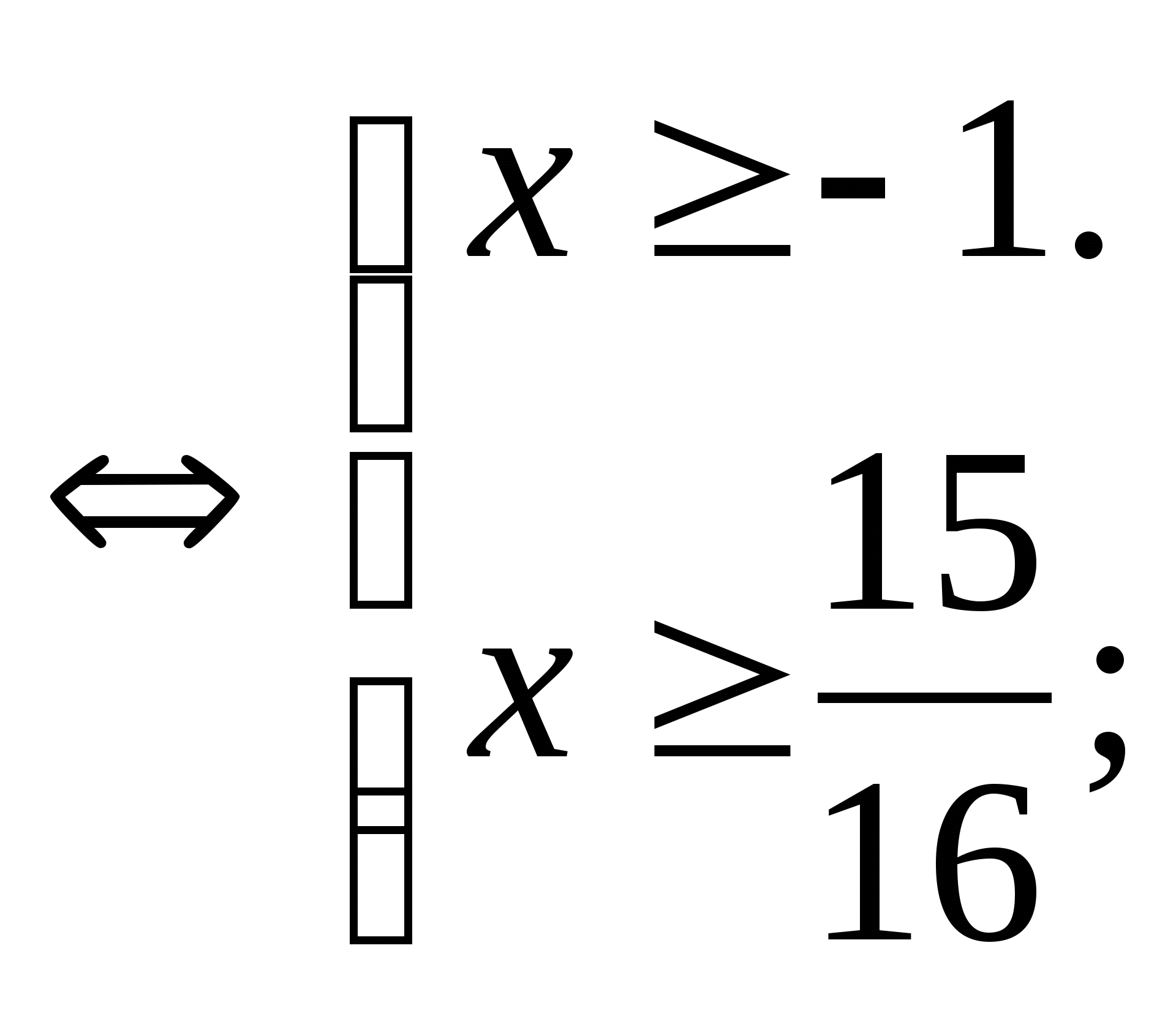
Пусть

, возведем в квадрат,

,

,

, возведем в квадрат,

,

,

,

,

- посторонний корень, т.к. .

,

x+1=1,

x=0.

Проверка: ,

6-1=5.

Ответ: 0.

л) .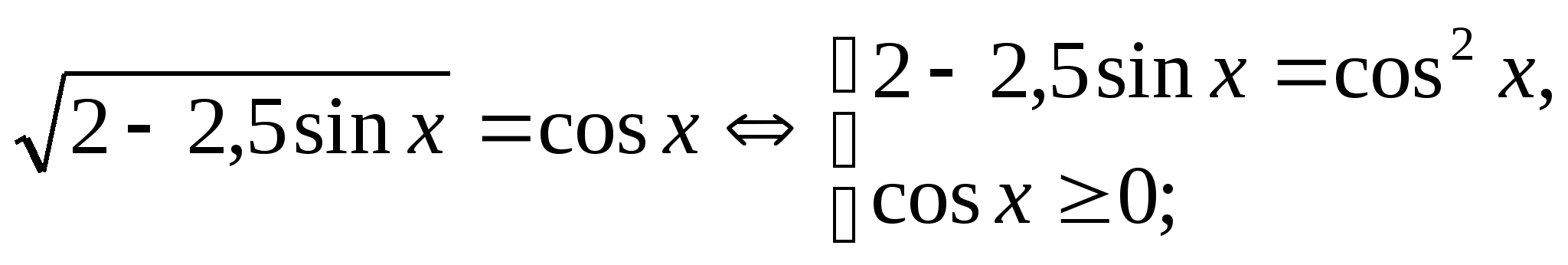

.

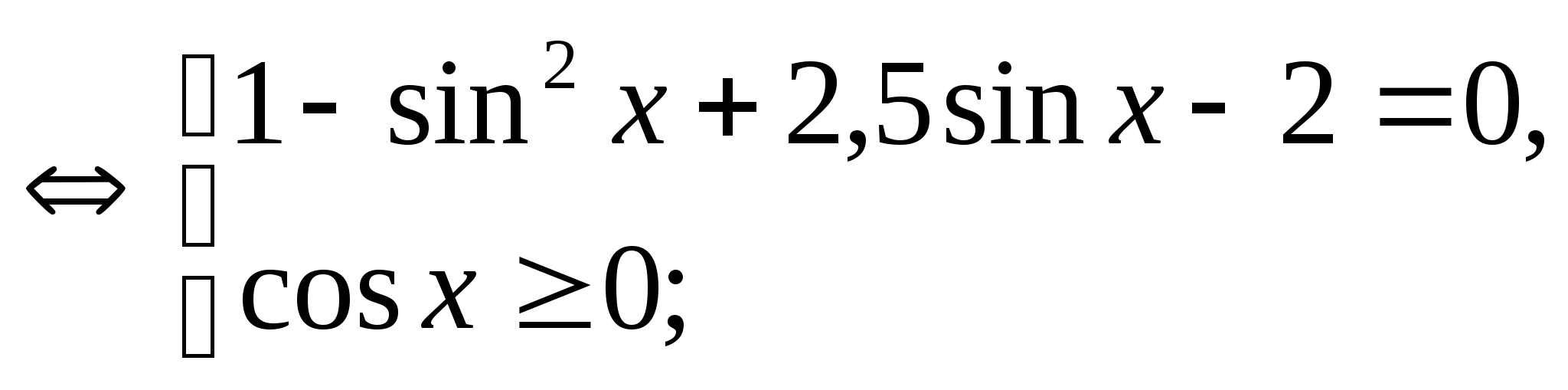
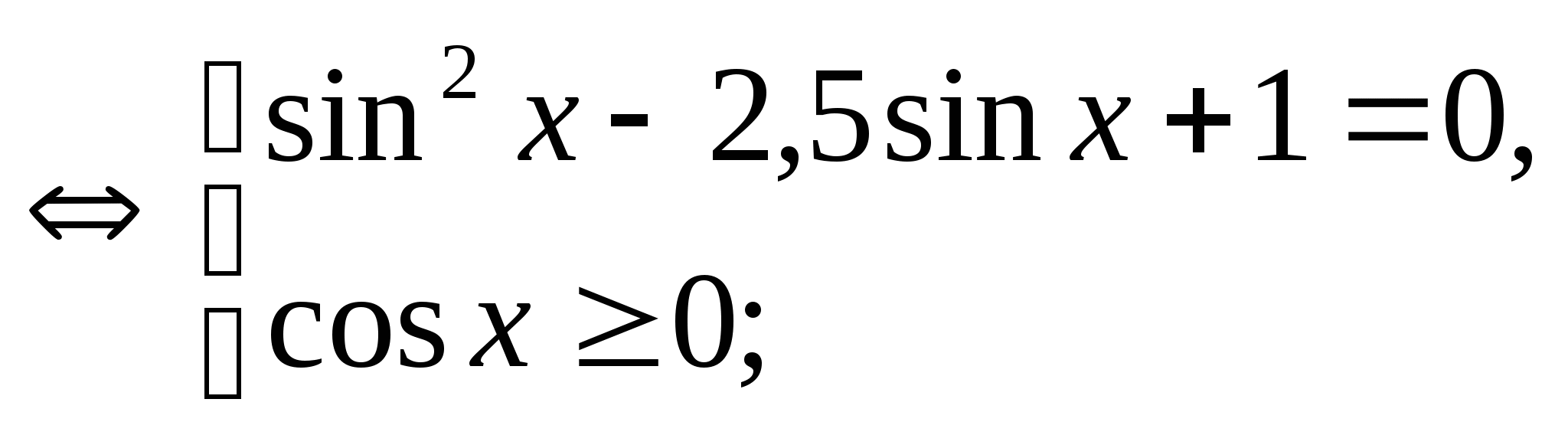
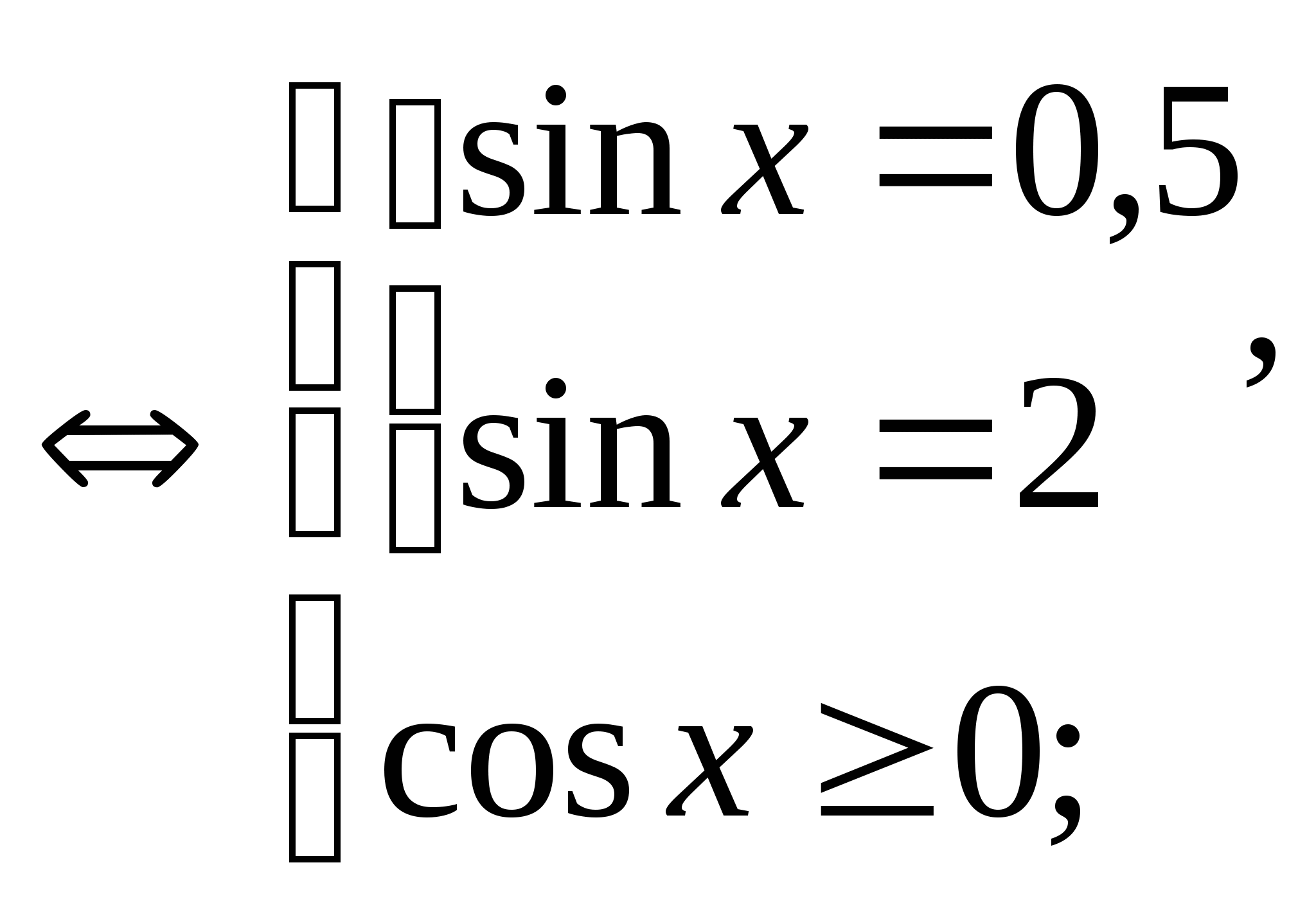
Ответ: .

Домашнее задание к 1-му семинару:

1) ;

2) ;

3) ;

4) ;

5) .