- Учителю
- Конспект урока по геометрии на тему: Второй признак равенства треугольников (7 класс)
Конспект урока по геометрии на тему: Второй признак равенства треугольников (7 класс)
УРОК № 18 (10.11.2016)
Предмет: геометрия, 7 класс
Тема урока: Второй признак равенства треугольников.
Цели урока:
-
Обучающая: изучить второй признак равенства треугольников, выработать навыки использования его при решении задач.Систематизировать, расширить и углубить знания учащихся о треугольнике, закрепить навыки и умения при решении задач, используя определения и теоремы по данной теме.
-
Развивающая: развивать математическую речь учащихся, их память, внимание, наблюдательность, умение сравнивать, обобщать, обоснованно делать выводы, развивать умение преодолевать трудности при решении задач, а также познавательный интерес учащихся.
-
Воспитательная: воспитание навыков контроля и самоконтроля, воспитание правильной самооценки, аккуратности, внимательности, положительное отношение к обучению, честности.
Тип урока: изучения нового материала
Ход урока:
1.Организационный момент
2.Повторение. Актуализация опорных знаний.
3.Объяснение нового материала.
4.Закрепление материала. Решение упражнений.
5. Итоги урока. Рефлексия.
6. Домашнее задание
1. Организационный момент. Приветствие. Мотивация.
«Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать».
Галилео Галилей
2 . Повторение. Актуализация опорных знаний.
Задание 1:
Заполнить пропуски так, чтобы получились предложения, соответствующие данному чертежу.
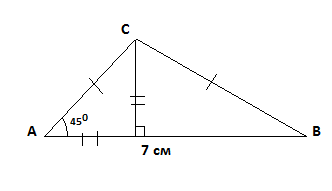
1.Градусная мера углов <А, <В, <АСН, <НСВ равна сорока пяти градусам.
2. На чертеже изображено три равных отрезка НВ, АН,СН, длина каждого из которых равна 3,5 см.
3. Изображенные на чертеже треугольники : АНС, АСВ равнобедренные. Они имеют по два равных угла с градусной мерой 45 градусов.
Задание 2:
Выделите условие и заключение в перечисленных утверждениях.
-
Если треугольники равны, то в них равны соответственные углы.
Условие:
Заключение:
2. Если треугольники равны, то равен и их периметр.
Условие:
Заключение:
3. В равнобедренном треугольнике найдутся две равные стороны.
Условие:
Заключение:
4. В равнобедренном треугольник углы при основании равны.
Условие:
Заключение:
5. В равнобедренном треугольнике медианы, проведённые к боковым сторонам равны между собой.
Условие:
Заключение:
Устно: 3
Вставьте в предложения подходящие слова так, чтобы получились верные утверждения.
-
Периметр равностороннего треугольника в три раза больше длины его стороны.
-
Если треугольник ABC и MNK равны, то в треугольнике ABC найдётся
угол равный углу NMK.
-
Если AK и BN - медианы треугольника ABC, то третья медиана этого треугольника пройдёт через точку пересечения медиан AK и BN
-
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
3 Объяснение нового материала.
Сегодня на уроке мы изучим второй признак равенства треугольника (по стороне и прилежащим к ним углам). (Записывают формулировку теоремы в тетрадь).
Если сторона и прилежащие к ней углы одного треугольника соответственно равны, стороне и прилежащим к ней углам другого треугольника то такие треугольники равны.
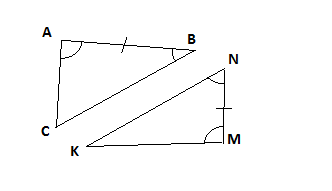 Дано:
Треугольник ABC, треугольник MNK, AB=MN, <A = <M, <B =
<N. Доказать: Треугольник ABC = треугольнику MNK
Дано:
Треугольник ABC, треугольник MNK, AB=MN, <A = <M, <B =
<N. Доказать: Треугольник ABC = треугольнику MNK
Доказательство:
-
Наложим треугольник ABC на треугольник MNK, так чтобы AB совместилось с MN, вершины C и K лежали по одну сторону от MN.
-
Так как AB = MN, то A совместится с M, вершина B - с вершиной N.
-
Луч AC совместится с MK, так как <A = <M, луч BC совместится с NK так как <B = <N.
-
Точка пересечения AC и BC совместится с точкой пересечения лучей MK и NK то есть C совместится с K.
-
Треугольник ABC и треугольник MNK полностью совместится, следовательно, треугольник ABC равен треугольнику MNK.
Ч.Т.Д
4 Закрепление изученного материала. Решение упражнений.
Задача № 1.
Отрезки AB и CD пересекаются в точке O.
Докажите равенство треугольников ACO и DOB если известно, что угол ACO равен углу DBO и BO=CO.
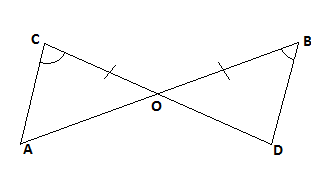
Проверка решения задачи
Решение:
Рассмотрим треугольник ACO и треугольник DBO:
BO=CO (по условию)
<ACO = < DBO (по условию)
<AOC = <DOB (вертикальные.)
Следственно треугольник ACO = треугольнику DBO по стороне и двум прилежащим к ней углам.
Задача № 2.
Отрезки AC и BD пересекаются в точке O.
Докажите равенство треугольников BAO и DCO, если известно, что угол BAO равен углу DCO, AO = CO.
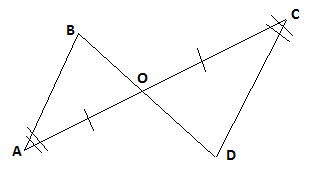
Проверка решения задачи
Решение:
Рассмотрим треугольник BAO и треугольник DCO.
AO = CO (по условию)
<BAO = <DCO (по условию)
<AOB = < COD (по вертик.)
Треугольник BAO = треугольнику DCO по стороне и двум прилежащим к ней углам.
Учебник (решение упражнений у доски) №121, №123
_5 Итоги урока. Рефлексия.
_6 Домашнее задание: п.19 выуч.теорему, стр. 41 №122, №124, 126 (доп-но).