Урок на тему правильные многоугольники

«Правильные многоугольники»

Обобщающий урок по геометрии.

9 класс.

Тема урока. Правильные многоугольники

План урока.

1. Оргмомент

2. Решение задач (несколькими способами).

3. Сообщение ученика «Правильные многоугольники в природе».

4. Решение задачи.

4. Практическая работа.

5. Итог урока.

Оборудование

Плакаты с изображением пчелиных сот, кристаллических решеток химических веществ, шаблоны правильных многоугольников: 3-угольников, 4-угольников, 6-угольников, 5-угольников.

Ход урока.

1 этап.

Цель урока :

• обобщить изученный материал;

• формировать умения применять математические знания к решению

• практических задач;

• развивать познавательную активность;

• творческие способности;

• воспитывать интерес к предмету.

2 этап.

Ребята, вы, знаете, что некоторые геометрические задачи можно решить с помощью разных способов.

Задача 1. У правильного треугольника радиус вписанной окружности в два раза меньше радиуса описанной окружности. Попробуйте, докажите.

Каждой группе предлагается решить задачу своим способом, используя:

1

Рис.1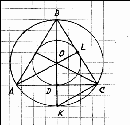

Рис.1группе: свойство медиан треугольника;

2 группе: свойство биссектрисы угла;

3 группе: понятие синуса угла;

4 группе: зависимость между стороной

правильного многоугольника и радиусом

описанной окружности;

5 группе: подобие треугольников.

На решение задач дается 5 мин. Далее каждая группа объясняет свой способ доказательства у доски по готовому чертежу.

Решение.

1 способ.

В правильном треугольнике центры вписанной и описанной окружности совпадают, биссектрисы являются медианами. Так как медианы точкой пересечения делятся в отношении 2:1, то

R : r = 2 : 1, т.е. R = 2r.

Вопрос. Какая окружность называется вписанной в многоугольник?

Ответ. Окружность касающаяся всех сторон многоугольника называется вписанной.

2 способ.

Рассмотрим треугольник ВАD. Биссектриса АО делит сторону ВD в отношении

, т.е. R=2r

Вопрос. Верно ли утверждение, что любой равносторонний треугольник является правильным?

Ответ. Верно.

3 способ.

В равнобедренном треугольнике АОС < АОС = 120° как центральный угол. Высота ОD является и биссектрисой, поэтому <DОС = 60° , а <ОСD= 30°. Следовательно,

Вопрос. Верно ли, что любой четырехугольник с равными сторонами является правильными?

Ответ. Нет, т.к. углы должны быть тоже равны.

4 способ.

Вопрос. Верно ли утверждение, что любой правильный многоугольник является выпуклым?

Ответ.

5 способ.

Вопрос. Какая окружность называется описанной около многоугольника?

Ответ. Если все вершины многоугольника лежат на окружности, то она называется описанной.

Может у вас есть еще какие-нибудь способы доказательства?

Эту задачу можно решить методом площадей:

S= BD AC= (R + r) a, S_ABC = 3S_AOC ( AOC=BOC=AOB)

S_ABC=3 ODAC= ra (R+r)a= ra, R+r=3r, R=2r

(заранее приготовлен на доске)

3 этап. Сообщение ученика.

Правильные многоугольники встречаются в природе.

Например, кристаллическая решетка некоторых химических элементов, драгоценных камней имеют форму правильных многогранников, у которых в основании лежат правильные многоугольники.

У хлорида натрия (поваренная соль) - правильная призма, у которой основание - квадрат, а у графита - правильная 6-тиугольная призма , основанием которой является правильный 6-тиугольник

Один из ярких примеров природных правильных многоугольников - пчелиные соты, которые представляют собой прямоугольник, покрытый (т.е. составленный без просветов и перекрытий) правильными шестиугольниками. На этих 6-угольниках пчелы наращивают из воска ячейки, представляющие собой прямые 6-угольные призмы (показать призму ).В них пчелы и откладывают мед, который является ценнейшим и питательнейшем продуктом питания, а затем снова покрывают сплошным прямоугольником из воска.

Чарльз Дарвин отмечает: «Далее этой ступени совершенства в архитектуре естественный отбор не мог вести, потому что соты пчел абсолютно совершенны с точки зрения экономии труда и воска».

Геометрия пчелиных сот, жизнь и деятельность пчел всегда привлекала внимание человека. ,,Странные общественные привычки и геометрические дарования пчел-, пишет известный математик Герман Вейль,- не могли не привлечь внимание и не вызвать восхищение людей, наблюдающих их жизнь и использовавших плоды их деятельности".На примере пчел мы убеждаемся, насколько гармонично устроен наш мир, как умна природа. Задача человека - беречь этот мир и разумно пользоваться его дарами.

Но не только в природе встречаются правильные многоугольники. Человек в своей практической деятельности научился использовать их красоту и рациональность в архитектуре, технике, в строительстве.

4 этап.

Как было замечено, пчелиные соты представляют собой прямоугольник, покрытый правильными 6-угольниками.

А почему пчелы выбрали именно 6-угольник?

Наверное для ответа нужно сравнить периметры разных многоугольников, имеющие одинаковые площади.

Задача 2. Пусть даны правильные треугольник, четырехугольник, шестиугольник. У какого из этих многоугольников периметр наименьший?

Рис.2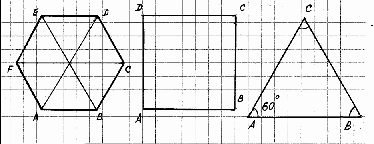

Решение.

Вывод по задаче. Итак, пчелы не зная математики, верно определили, что правильный 6-угольник имеет наименьший периметр среди фигур равной площади. Строя 6-угольные ячейки, пчелы наиболее экономно используют площадь внутри небольшого улья и воск для изготовления ячеек.

5 этап. Практическая работа.(по группам)

Можно ли без просветов покрыть плоскость многоугольниками, если этими многоугольниками являются правильные

а) 3-угольники,

б) 4-угольники,

в) 5-угольники,

г) 12-угольники,

д) 3-угольники, 4-угольники и 6-угольники.

Готовые орнаменты вывешиваем. Обсуждаем.

Вопрос. Где человек может использовать умение покрывать плоскость правильными многоугольниками?

Ответ. При составлении различных орнаментов, паркета и т. д. можно использовать покрытие плоскости правильными многоугольниками.

7 этап.

Итог урока.

Итак, мы познакомились с правильными многоугольниками, научились вычислять сторону правильного многоугольника., его периметр, площадь, а так же учились строить некоторые многоугольники точным методом с помощью линейки и циркуля. Но не любой многоугольник можно построить этим методом. Например, 9-угольник. Для того, чтобы его построить нужно воспользоваться приближенными методами. С некоторыми из них предлагаю вам познакомиться дома по данному пособию. Тут же на последней странице записано домашнее задание обязательное, которое заключается в решении 3-х номеров по учебнику и необязательное домашнее задание-построение правильного многоугольника выше описанным способом.

Оценки за урок!!!!!!

Похвала!!!!!