Рабочие программы Математика 7,8,10 классы

РАБОЧАЯ ПРОГРАММА

по алгебре

10 класс

(2016 - 2017 учебный год)

Пояснительная записка

Рабочая программа учебного курса «Алгебра» разработана для учащихся 10 А класса и направлена на реализацию обязательной части учебного плана.

Рабочая программа учебного курса предусматривает реализацию:

1. Федерального компонента I поколения по предмету «Математика»;

2. Регионального компонента основного общего образования:

А) через формирование компетенций:

• образовательных;

• предметных;

• информационно-методологических;

• коммуникативных;

• организационных;

• общекультурных.

Б) путём оценивания качества образования как совокупности трёх составляющих:

• предметно-информационной (просвещенность),

• деятельностно-коммуникативной (обученность),

• ценностно-ориентационной (воспитанность).

3. Школьного компонента - соответствие целевым ориентирам школы в соответствии с программой развития МБОУ «СОШ №3».

Рабочая программа учебного курса подготовлена для обеспечения образовательных запросов учащихся, связанных с углублением знаний, полученных при изучении математики в 5-9 классах. Является логическим продолжением программы для 9-го класса (Учеб. для 9 кл. общеобразоват. учреждений / Ю. Н, Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского. - 9-е изд. - М.: Просвещение, 2012. - 238 с.: ил.)

Нормативные документы и примерные программы, лежащие в основе курса:

Федеральные документы;

1. Конституция РФ.

2. Федеральный закон от 29.12.2012 № 273-ФЗ "Об образовании в Российской Федерации".
   
   3. Приказ Министерства образования Российской Федерации от 9.03.2004 № 1312 (в редакции приказов Минобрнауки РФ от 20.08.2008, от 30.08.2010 № 889, от 03.06.2011 № 1994, от 01.02.2012 № 74) «Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования».
   
   4. Санитарно-эпидемиологических правил и нормативов СанПиН 2.4.2.2821-10 "Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях" (Постановление Главного государственного санитарного врача Российской Федерации от 29 декабря 2010 г. N189).

5. Методические письма по предмету.

Региональные:

1. Закон об образовании Республики Адыгея от 27 декабря 2013 года №264.

2. Республиканские методические письма/приказы по предмету.

Школьные:

1. Устав МБОУ «СОШ №3»

2. Основная образовательная программа основного общего образования МБОУ «СОШ№3» на 2014-2015 учебный год.

3. Программа развития МБОУ «СОШ №3» «Школьник-Гражданин-Россиянин» на 2011-2015гг.

4. Школьные локальные акты.

5. Методические рекомендации Методического совета школы.

Изучение математики на ступени основного общего образования направлено на достижение следующих целей:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

Основные развивающие и воспитательные цели

Развитие:

• ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

• математической речи;

• сенсорной сферы;

• внимания; памяти;

• навыков само и взаимопроверки.

Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.

Воспитание:

• культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;

• волевых качеств;

• коммуникабельности;

• ответственности.

Программа рассчитана на 3 часа в неделю (105 ч. в году), 35 рабочих недель. В планировании учтено прохождение обязательного минимума содержания и соответствие программе по математике для основной средней школы.

Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных, контрольных, работ и математических диктантов (по 10 - 15 минут) в конце логически законченных блоков учебного материала. Итоговая аттестация предусмотрена в виде экзаменационной.

Рабочая программа учебного курса подготовлена для обеспечения образовательных запросов учащихся 10 класса, с учётом возрастных особенностей, выявленных в процессе изучения индивидуальных интересов обучающихся, с учётом состояния здоровья, уровня мотивации школьников.

Результаты обучения

Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие основную школу, и достижение которых является обязательным условием положительной аттестации ученика за курс основной школы.

Рабочая программа ориентирована на усвоение обязательного минимума математического образования, позволяет работать без перегрузок в классе с детьми разного уровня обучения и интереса к математике.

В основе построения программы лежат принципы единства, преемственности, вариативности, выделения понятийного ядра, деятельностного подхода, системности.

Содержание обучения

Основные разделы: курс «Алгебра и начала анализа. 10 класс»:

«Действительные числа», «Степенная функция», «Показательная функция», «Логарифмическая функция», «Тригонометрические формулы»,

«Тригонометрические уравнения», «Итоговое повторение»;

1.Действительные числа

Целые и рациональные числа. Действительные числа. бесконечно убывающая геометрическая прогрессия. Арифметический корень натуральной степени. Степень с рациональным и действительным показателями.

Основная цель - обобщить и систематизировать знания о действительных числах; сформировать понятие степени с действительным показателем; научить применять определения арифметического корня и степени, а также их свойства при выполнении вычислений и преобразовании выражений.

2.Степенная функция

Степенная функция, ее свойства и график. Взаимно обратные функции. Равносильные уравнения и неравенства. Иррациональные уравнения. Иррациональные неравенства.

Основная цель - обобщить и систематизировать известные из курса алгебры основной школы свойства функций; изучить свойства степенных функций с натуральным и целым показателями и научить применять их при решении уравнений и неравенств; сформировать понятие равносильности уравнений, неравенств, систем уравнений и не равенств.

3.Показательная функция

Показательная функция, ее свойства и график. Показа тельные уравнения. Показательные неравенства. Системы показательных уравнений и неравенств.

Основная цель - изучить свойства показательной функции; научить решать показательные уравнения и не равенства, простейшие системы показательных уравнений.

4.Логарифмическая функция

Логарифмы. Свойства логарифмов. Десятичные и натуральные логарифмы. Логарифмическая функция, ее свойства и график. Логарифмические уравнения. Логарифмические неравенства.

Основная цель - сформировать понятие логарифма числа; научить применять свойства логарифмов при решении уравнений; изучить свойства логарифмической функции и научить применять ее свойства при решении простейших логарифмических уравнений и неравенств.

5.Тригонометрические формулы

Радианная мера угла. Поворот точки вокруг начала координат. Определение синуса, косинуса и тангенса угла. Знаки синуса, косинуса и тангенса. Зависимость между синусом, косинусом и тангенсом одного и того же угла. Тригонометрические тождества. Синус, косинус и тангенс углов а и -а. Формулы сложения. Синус, косинус и тангенс двойного угла. Синус, косинус и тангенс половинного угла. Формулы приведения. Сумма и разность синусов. Сумма и разность косинусов.

Основная цель - сформировать понятия синуса, косинуса, тангенса, котангенса числа; научить применять формулы тригонометрии для вычисления значений тригонометрических функций и выполнения преобразований тригонометрических выражений; научить решать простейшие тригонометрические уравнения sin x = a, cos x = а при а = 1, -1, 0.

6.Тригонометрические уравнения

Уравнения cos x = a, sin x = a, tg x = а. Решение тригонометрических уравнений. Примеры решения простейших тригонометрических неравенств.

Основная цель - сформировать умение решать простейшие тригонометрические уравнения; ознакомить с некоторыми приемами решения тригонометрических уравнений.

7.Повторение и решение задач

Тематическое планирование учебного материала.

«Алгебра и начала анализа».

Кол-во контрольных работ

1

Действительные числа

11

1

2

Степенная функция

11

1

3

Показательная функция

12

1

4

Логарифмическая функция

16

1

5

Тригонометрические формулы

20

1

6

Тригонометрические уравнения

21

1

7

Итоговое повторение

1

1

Итого

7 тем

105

7

Курс алгебры и начал анализа X класса характеризуется содержательным раскрытием понятий, утверждений и методов, относящихся к началам анализа, выявлением их практической значимости. При изучении вопросов анализа широко используются наглядные соображения. Уровень строгости изложения определяется с учетом общеобразовательной направленности изучения начал анализа и согласуется с уровнем строгости приложений изучаемого материала в смежных дисциплинах. Характерной особенностью курса является систематизация и обобщение знаний учащихся, закрепление и развитие умений и навыков учащихся, полученных в курсе алгебры, что осуществляется как при изучении нового материала, так и при проведении обобщающего повторения.

Принципиальным положением организации математического образования становится дифференциация обучения в школе. При этом достижение уровня обязательной подготовки становится непременной обязанностью ученика в его учебной работе. В организации учебно-воспитательного процесса важную роль играют задачи. В обучении математики они являются и целью, и средством обучения и математического развития школьников. Организуя решение задач, следует иметь в виду, что теоретический материал осознается и осваивается преимущественно в процессе решения задач, организуя их решение, целесообразно использовать дифференцированный подход к учащимся, основанный на достижении обязательного уровня подготовки. Это способствует нормализации нагрузки школьников, обеспечивая их посильной работой, и формирует у них положительное отношение к учебе.

Важным условием правильной организации учебно-воспитательного процесса является выбор рациональной системы методов и приемов обучения. Необходимо реализовать сбалансированное сочетание традиционных и новых методов обучения, оптимизировать применение объяснительно-иллюстративных и эвристических методов, использование технических средств. Учебный процесс необходимо ориентировать на рациональное сочетание устных и письменных видов работы, как при изучении теории, так и при решении задач. Внимание должно быть направлено на развитие речи учащихся, формирование у них навыков умственного труда - планирование своей работы, поиск рациональных путей ее выполнения, критическую оценку результатов.

В школе математика является опорным предметом средней школы: она обеспечивает изучение других дисциплин, прежде всего предметов естественно-научного цикла, в частности физики, основ информатики и вычислительной техники, химии. Например, на уроках физики, изучение понятий и законов механики осуществляется с использованием знаний о векторах, действиях с ними, координатах точки, проекциях вектора, линейной функции и ее графике, квадратных уравнениях, окружности, касательной к ней. Практические умения и навыки математического характера необходимы для трудовой подготовки школьников. При изучении отдельных тем курса математики возможна опора на знания, полученные учащимися на других предметах. Например, знания, полученные при изучении механики: о мгновенной скорости развиваются при введении производной; о свободных колебаниях - используются при рассмотрении дифференциальных уравнений; о перемещении в равноускоренном движении, о работе переменной силы - при изучении интеграла.

Требования к математической подготовке учащихся:

Вычисления и преобразования:

В результате изучения курса математики учащиеся должны:

• находить значение корня, степени, логарифма, значения тригонометрических выражений на основе определений. С помощью калькулятора или таблиц;

• выполнять тождественные преобразования иррациональных, степенных, показательных, логарифмических и тригонометрических выражений;

Уравнения и неравенства:

В результате изучения курса математики учащиеся должны:

• решать иррациональные, показательные, логарифмические, и тригонометрические уравнения;

• решать системы уравнений с двумя неизвестными;

• решать рациональные, показательные, логарифмические неравенства;

• иметь представление о графическом способе решения уравнений и неравенств;

Функции:

В результате изучения курса математики учащиеся должны:

• определять значение функции по значению аргумента при различных способах задания функции;

• иметь наглядные представления об основных свойствах функций; иллюстрировать их с помощью графических изображений;

• изображать графики основных элементарных функций; опираясь на график описывать свойства этих функций; уметь использовать свойства этих функций для сравнения и оценки ее значений;

• понимать механический и геометрический смысл производной; находить производные элементарных функций, пользуясь таблицей производной и правилами дифференцирования суммы, произведения и частного, формулой производной функции вида ; в несложных ситуациях применять производную для исследования функции на монотонность и экстремумы, для нахождения наибольших и наименьших значений функций и для построения графиков;

• понимать смысл понятия первообразной, находить первообразные для суммы функций и произведения функции на число;

• вычислять в простейших случаях площадь криволинейной трапеции.

Требования к уровню усвоения дисциплины.

Рекомендации по оценке знаний, умений и навыков учащихся по математике.

Опираясь на эти рекомендации, учитель оценивает знания, умения и навыки учащихся с учетом их индивидуальных особенностей.

1. Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.

2. Основными формами проверки знаний и умений, учащихся по математике являются письменная контрольная работа и устный опрос.

3. Среди погрешностей выделяются ошибки и недочеты.

Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе.

К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, которые в программе не считаются основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения: неаккуратная запись, небрежное выполнение чертежа.

4. Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.

Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью.

Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно, выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.

5. Оценка ответа учащихся при устном и письменном опросе производится по пятибалльной системе.

6. Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося, за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им задания.

7. Итоговые отметки (за тему, четверть, курс) выставляются по состоянию знаний на конец этапа обучения с учетом текущих отметок.

Оценка устных ответов учащихся.

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;

• продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость использованных при ответе умений и навыков;

• отвечал самостоятельно без наводящих вопросов учителя.

• Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Ответ оценивается отметкой «4», если он удовлетворен в основном требованиям на отметку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившие математического содержания ответа, исправленные по замечанию учителя.

• допущены ошибки или более двух недочетов при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Отметка «3» ставится в следующих случаях:

• неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»).

• имелись затруднения или допущены ошибки в определении понятий и, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при знании теоретического материала выявлена недостаточная сформированность умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Оценка «1» ставится в случае, если:

• ученик обнаружил полное незнание и непонимание изучаемого материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.

Оценка письменных контрольных работ учащихся.

Отметка «5» ставится в следующих случаях:

• работа выполнена полностью.

• в логических рассуждениях и обоснованиях нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала);

Отметка «4» ставится, если:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умения обосновывать рассуждения не являлись специальным объектом проверки);

• допущена одна ошибка или два-три недочета в выкладках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки);

Отметка «3» ставится, если:

• допущены более одной ошибки или более двух- трех недочетов в выкладках, чертежах или графика, но учащийся владеет обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что учащийся не владеет обязательными знаниями по данной теме в полной мере.

Отметка «1» ставится, если:

• работа показала полное отсутствие у учащегося обязательных знаний, умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Информационно - методическое обеспечение

Для учащихся:

1. Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.

« Алгебра и начала анализа» - учебник для 10 -11 классов общеобразовательных учреждений.- Москва: Просвещение, 2011г.

2. А.П. Карп

«Сборник задач по алгебре и началам анализа 10 - 11 класс». Москва: «Просвещение» 2011 год.

3. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С1/Под ред. А.Л. Семёнова и И.В. Ященко. - М.:МЦНМО, 2016. - 120с

4. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С2/Под ред. А.Л. Семёнова и И.В. Ященко. - М.:МЦНМО, 2016. - 120с

5. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С3/Под ред. А.Л. Семёнова и И.В. Ященко. - М.:МЦНМО, 2016. - 120с

6. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С4/Под ред. А.Л. Семёнова и И.В. Ященко. - М.:МЦНМО, 2016. - 120с

7. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С5/Под ред. А.Л. Семёнова и И.В. Ященко. - М.:МЦНМО, 2016. - 120с

8. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С6/Под ред. А.Л. Семёнова и И.В. Ященко. - М.:МЦНМО, 2016. - 120с

9. Лаппо, Л.Д. ЕГЭ 2016. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ/Л.Д.Лаппо, М.А. Попов. - М.: Издательство «Экзамен», 2012. - 63,с. (Серия «ЕГЭ. Практикум»)

10. ЕГЭ 2012. Математика. Типовые тестовые задания/ И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров, В.С. Панферов, С.Е. Посицельский, А.В. Семёнов, А.Л. Семёнов, М.А. Семёнова, И.Н. Сергеев, В.А. Смирнов, С.А. Шестаков, Д.Э.Шноль, И.В. Ященко; под ред. А.Л. Семёнова, И.В. Ященко. - М.: Издательство «Экзамен», 2016. - 55, с. (Серия «ЕГЭ 2011. Типовые тестовые задания»)

11. ЕГЭ 2012. Математика: тренировочные задания/ Т.А. Корешкова, В.В. Мирошин, Н.В. Шевелёва. - М.: Эксмо, 2016. - 80 с. - (ЕГЭ. Тренировочные задания).

12. ЕГЭ - 2012. Математика: типовые экзаменационные варианты: 30 вариантов/под ред. А.Л.Семёнова, И.В. Ященко. - М.: Национальное образование, 2014. - 240 с. - (ЕГЭ-2011. ФИПИ - школе)

Для учителя:

1. Г.И. Григорьева

Пособие для учителя « Алгебра» 10 класс. Волгоград : « Учитель» 2011 год.

2. А.П. Карп

«Сборник задач по алгебре и началам анализа 10 - 11 класс» .Москва: «Просвещение» 2011 год.

3. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С1/Под ред. А.Л. Семёнова и И.В. Ященко. - М.:МЦНМО, 2016. - 120с

4. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С2/Под ред. А.Л. Семёнова и И.В. Ященко. - М.:МЦНМО, 2016. - 120с

5. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С3/Под ред. А.Л. Семёнова и И.В. Ященко. - М.:МЦНМО, 2016. - 120с

6. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С4/Под ред. А.Л. Семёнова и И.В. Ященко. - М.:МЦНМО, 2016. - 120с

7. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С5/Под ред. А.Л. Семёнова и И.В. Ященко. - М.:МЦНМО, 2016. - 120с

8. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С6/Под ред. А.Л. Семёнова и И.В. Ященко. - М.:МЦНМО, 2016. - 120с

9. Лаппо, Л.Д. ЕГЭ 2011. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ/Л.Д.Лаппо, М.А. Попов. - М.: Издательство «Экзамен», 2015. - 63,с. (Серия «ЕГЭ. Практикум»)

10. ЕГЭ 2012. Математика. Типовые тестовые задания/ И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров, В.С. Панферов, С.Е. Посицельский, А.В. Семёнов, А.Л. Семёнов, М.А. Семёнова, И.Н. Сергеев, В.А. Смирнов, С.А. Шестаков, Д.Э.Шноль, И.В. Ященко; под ред. А.Л. Семёнова, И.В. Ященко. - М.: Издательство «Экзамен», 2015. - 55, с. (Серия «ЕГЭ 2012. Типовые тестовые задания»)

11. ЕГЭ 2012. Математика: тренировочные задания/ Т.А. Корешкова, В.В. Мирошин, Н.В. Шевелёва. - М.: Эксмо, 2016. - 80 с. - (ЕГЭ. Тренировочные задания).

12. ЕГЭ - 2012. Математика: типовые экзаменационные варианты: 30 вариантов/под ред. А.Л.Семёнова, И.В. Ященко. - М.: Национальное образование, 2014. - 240 с. - (ЕГЭ-2011. ФИПИ - школе)

13. Б.М. Ивлев, С.М. Саакян, С.И. Шварцбург

« Дидактические материалы по алгебре и началам анализа» 10 класс. Москва «Просвещение» 2011 год.

14. Б.Г. Зив, В.А Гольдич Дидактические материалы по алгебре и началам анализа для 10 класса, СПб.: «Петроглиф», «Виктория плюс», 2011

15. Шабунин М.И. и др.

Алгебра и начала анализа. Дидактические материалы для 10-11 кл., 4 изд., М.: Мнемозина, 2011.- 251с.

16. Н.Е. Федорова, М.В. Ткачева Изучение алгебры и начал анализа в 10-11 кл. - М.: Просвещение, 2010. - 205с.

Программное обеспечение:

1. Алгебра и начала анализа 10-11 классы

2. Алгебра, 7-11 классы

3. Математика, 5-11 классы. Практикум

4. ПМК «Математика. Средняя школа. Ч 3»

5. Уроки алгебры Кирилла и Мефодия (10-11 классы)

6. Физикон. Математика: Алгебра

7. Физикон. Математика: Функции и графики

Контрольная работа №1 по теме:

«Действительные числа»

Вариант №1. Обязательная часть

1. Бесконечно убывающая геометрическая прогрессия. Формула суммы.

2. Вычислите:а)

   в)

   б)

   г)

3. Упростите выражения:а)

   б)

   в)

4. Разложите на множители: a - 4.

5. Сократите дробь:

Дополнительная часть

1. Сравните числа a и b, если:

2. Упростите выражение:

Вариант №2. Обязательная часть

1. Арифметический корень натуральной степени. Свойства.

2. Вычислите:а)

   в)

   б)

   г)

3. Упростите выражения:а)

   б)

   в)

4. Разложите на множители:

5. Сократите дробь:

Дополнительная часть

1. Сравните числа a и b, если:

2. Упростите выражение:

Контрольная работа №2 по теме:

«Степенная функция»

Вариант №1.

1. Найти область определения функции .

2. Изобразить эскиз графика функции .

1. Указать область определения и множество значений функции.

2. Выяснить, на каких промежутках функция убывает.

3. Сравнить числа и .

3. Решить уравнение:

2)

3)

4)

4. Решить неравенство: .

4. Найти функцию, обратную к ; указать её область определения и множество значений. На одном рисунке построить графики данной функции и функции, обратной к данной.

Вариант №2

1. Найти область определения функции .

2. Изобразить эскиз графика функции .

1. Указать область определения и множество значений функции.

2. Выяснить, на каких промежутках функция возрастает.

3. Сравнить числа и .

3. Решить уравнение:

2);

3);

4)

4. Решить неравенство: .

4. Найти функцию, обратную к ; указать её область определения и множество значений. На одном рисунке построить графики данной функции и функции, обратной к данной.

Контрольная работа №3 по теме:

«Показательная функция»

Вариант №1

1. Решить уравнение:1); 2).

2. Решить неравенство .

3. Решить систему уравнений

4. Решить неравенство:

1); 2).

5. Решить уравнение .

6. Решите уравнение: .

В ответе укажите корень уравнения или сумму корней, если их несколько.

Вариант №2

1. Решить уравнение:1); 2).

2. Решить неравенство .

3. Решить систему уравнений

_ 4. Решить неравенство:

1); 2).

55. Решить уравнение .

6. Решите уравнение: .

В ответе укажите корень уравнения или сумму корней, если их несколько.

Контрольная работа №4 по теме:

«Логарифмическая функция»

Вариант №1

1. Вычислите:.

2. При каких значениях х имеет смысл выражение:

а);

б)

3. Решите уравнение:

4. Упростите: a0,a1.

5. Дано:. Найти: .

Вариант №2

1. Вычислите: .

2. При каких значениях x имеет смысл выражение:

а) б)

3. Решите уравнение:

4. Упростите: a0,a1.

5. Дано: Найти:

Контрольная работа №5 по теме:

«Тригонометрические формулы»

Вариант №1

1. Решите уравнение:

.

2. Упростите выражение:

а);

б);

в).

3. Пустьуглы треугольника. Докажите тождество:

.

Вариант №2

1. Решите уравнение:

.

2. Упростите выражение:

а);

б);

в).

3. Пустьуглы треугольника. Докажите тождество:

.

Контрольная работа №6 по теме:

«Тригонометрические уравнения»

Вариант №1

1. Решите уравнение: sin x -=0

2. Решите уравнение: cos 2x=1

3. Укажите уравнение, которому соответствует решение: :

1) tg x = 1; 2) cos x = 0; 3) sin x = -1; 4) ctg x =.

4. На каком из рисунков показано решение неравенства: cos x <?

1) 2) 3) 4)

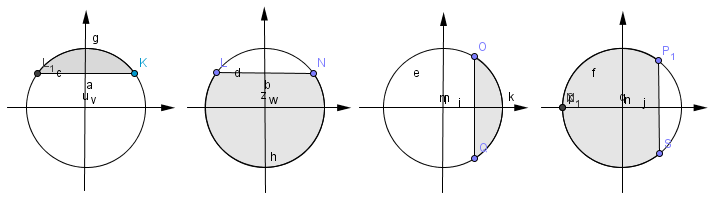
5. Решите неравенство: tg x ≥:

6. Решите уравнение: 6sin² x + sin x - 1 = 0

7. Решите уравнение: 2sin² x -sin 2x =0

Вариант №2

1. Решите уравнение: sin x +=0

2. Решите уравнение: ctg (x+)=

3. Укажите уравнение, которому соответствует решение: :

1) ctg x = -1; 2) cos x = 0; 3) cos x = -1; 4) tg x = 1.

4. На каком из рисунков показано решение неравенства: sin x ≥?

1) 2) 3) 4) 4)

5. Решите неравенство: ctg x ≥

6. Решите уравнение: cos² x - 4sin x + 3 = 0

7. Решите уравнение: sin² x -3sin x cos x =0

Критерии и нормы оценки знаний, умений, навыков

по математике.

Оценка устных ответов учащихся.

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;

• продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость использованных при ответе умений и навыков;

• отвечал самостоятельно без наводящих вопросов учителя.

Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Ответ оценивается отметкой «4», если он удовлетворен в основном требованиям на отметку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившие математического содержания ответа, исправленные по замечанию учителя.

• допущены ошибки или более двух недочетов при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Ответ оценивается отметкой «3», если ученик:

• неполно или непоследовательно раскрыл содержание материала, но показал общее понимание вопроса и продемонстрировал умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»).

• имелись затруднения или допущены ошибки в определении понятий и использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при знании теоретического материала выявлена недостаточная сформированность умений и навыков.

Ответ оценивается отметкой «2», если ученик:

• не раскрыл основное содержание учебного материала;

• обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;

• допустил ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Оценка письменных работ

Оценка «5» ставится, если:

- работа выполнена полностью;

- в логических рассуждениях и обоснованиях решения нет пробелов, ошибок;

-в решении нет математических ошибок (возможна одна неточность, описка).

Оценка «4» ставится, если:

- работа выполнена полностью, но обоснования шагов решения недостаточны (если умения обосновывать рассуждения не являлись специальным объектом проверки);

- допущена одна ошибка, или есть два-три недочета в выкладках, рисунках, чертежах, графиках и т.д (если умения обосновывать рассуждения не являлись специальным объектом проверки).

Оценка «3» ставится, если:

- допущено более одной ошибки или более двух-трех недочетов в выкладках, рисунках, чертежах, графиках, но учащийся обладает обязательными умениями по проверяемой теме.

Оценка «2» ставится, если:

- допущены существенные ошибки, показавшие, что учащийся не обладает обязательными умениями по данной теме в полной мере.