Обобщающая таблица по теме Четырехугольники

ЧЕТЫРЕХУГОЛЬНИКИПараллелограмм

Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны

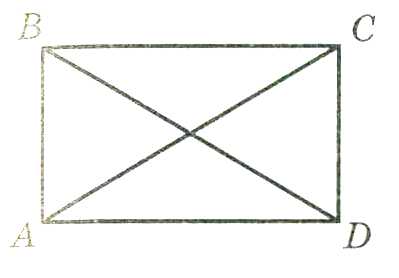
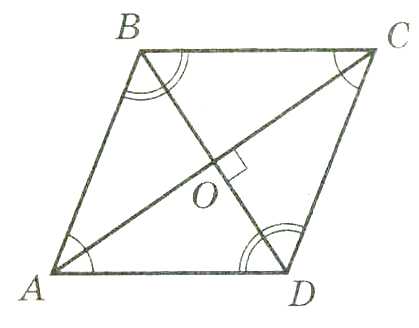
1.Диагональ параллелограмма делит его на два равных треугольника.

2.Противоположные стороны и противоположные углы параллелограмма равны.

3.Диагонали параллелограмма в точке пересечения делятся пополам.

4.Точка пересечения диагоналей является центром симметрии параллелограмма.

5. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180⁰.

6.Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

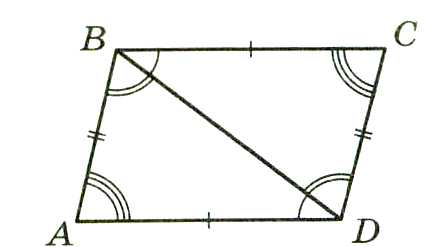
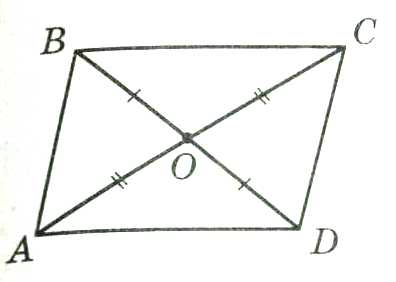
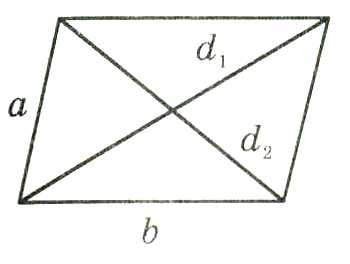
∆ABC=∆CDB AO=OC;BO=OD d₁²+d₂²=2a²+2b²

∟A=∟C; ∟A+∟B=180⁰;

∟B=∟D; ∟B+∟C=180⁰

AB=CD;BC=AD

1. Если диагонали четырехугольника точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.

2.Если противоположные стороны четырехугольника равны друг другу, то этот четырехугольник - параллелограмм.

3. Если в четырехугольнике противоположные стороны равны и параллельны, то этот четырехугольник - параллелограмм.

4. Если противоположные углы четырехугольника равны, то этот четырехугольник - параллелограмм.

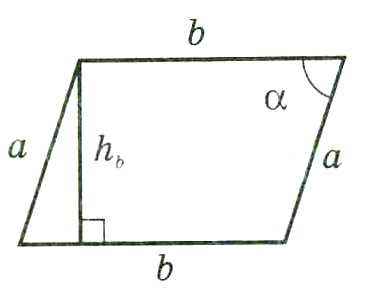
Площадь параллелограмма равна произведению его сторон на высоту, проведенную к этой стороне.

Площадь параллелограмма можно найти также по формулам:

Прямоугольник

Прямоугольник - это параллелограмм, у которого все углы равны.

1.Диагонали прямоугольника равны.

2. Диагонали прямоугольника точкой пересечения делятся пополам.

3. В прямоугольнике противоположные стороны равны.

1.Если ABCD - параллелограмм и ∟A = 90⁰, то ABCD - прямоугольник.

2. Если ABCD - параллелограмм и AС = BD, то ABCD - прямоугольник.

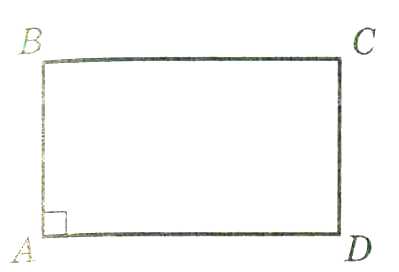
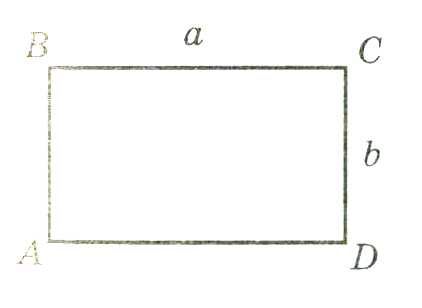
Площадь прямоугольника равна произведению его смежных сторон.

Ромб

Ромб - это параллелограмм, у которого все стороны равны

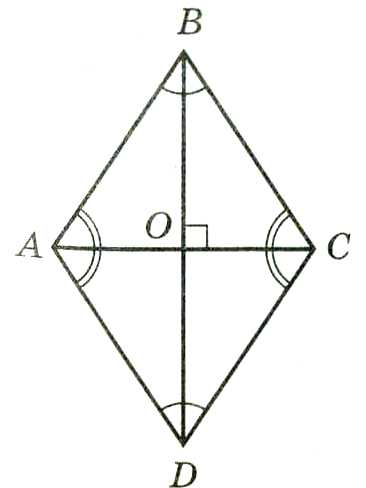
1. Диагонали ромба делят его на четыре равных прямоугольных треугольника.

2. Диагональ ромба делит его на два равных равнобедренных треугольника.

3. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Ромб имеет все свойства параллелограмма

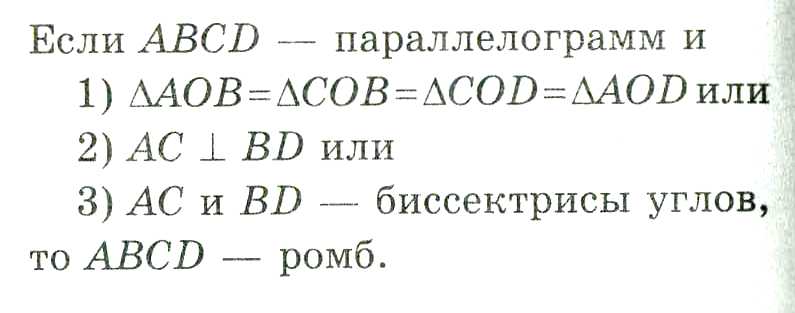
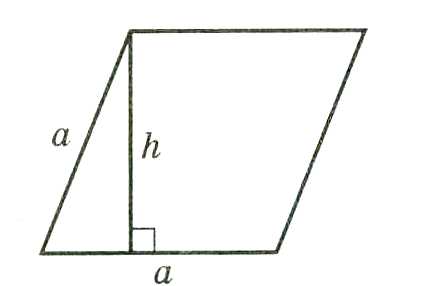
Площадь ромба равна произведению высоты на сторону:

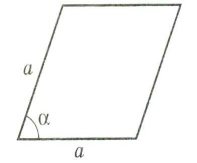
Площадь ромба равна произведению квадрата стороны на синус угла ромба:

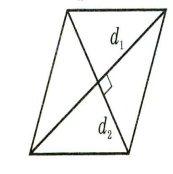
Площадь ромба равна половине произведения диагоналей:

Квадрат

Квадрат - это прямоугольник, у которого все стороны равны. Квадрат - это ромб, у которого все углы прямые.

Квадрат имеет все свойства ромба и прямоугольника.

Трапеция

Трапеция - четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Параллельные стороны называются основаниями, а две другие - боковыми.

1. Сумма углов прилежащих к боковой стороне равна 180⁰.

2. Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.

Средняя линия трапеции параллельна её основаниям и равна полусумме длин оснований.

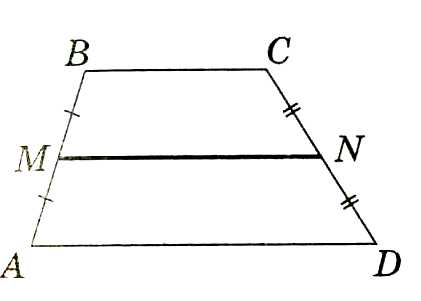
DC║MN║AD; MN=.

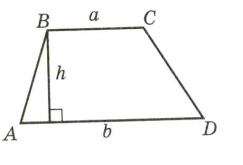
Площадь трапеции равна произведению полусуммы длин основания на высоту

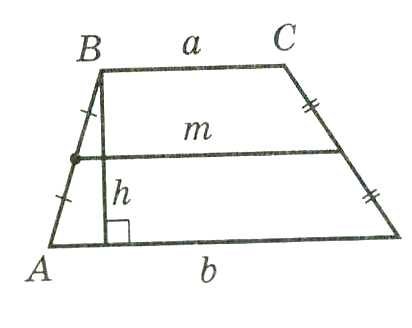
Площадь трапеции равна произведению её средней линии на высоту: m , где - средняя линия трапеции.

Равнобедренная трапеция-трапеция, у которой боковые стороны равны.

1.Углы при основании равнобедренной трапеции равны, т.е.∟A=∟ D;∟B=∟C.

2. AF=ED=;

3. AE=FD=.

4.Диагонали равнобедренной трапеции равны:AC=BD.

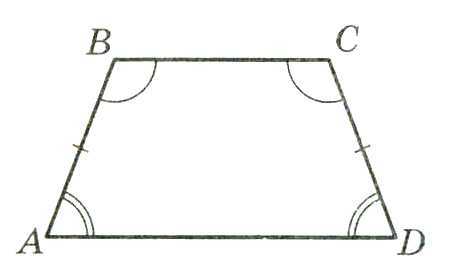
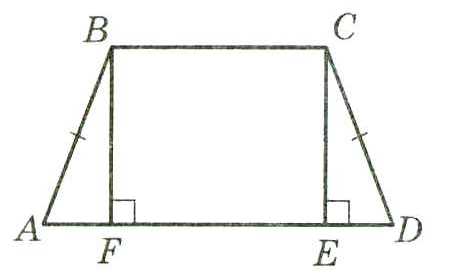
Если выполняется одно из утверждений 1-3, то трапеция равнобедренная.

Площадь см. трапеция

Прямоугольная трапеция-трапеция, у которой один угол прямой.

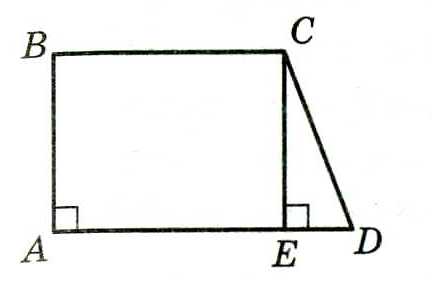
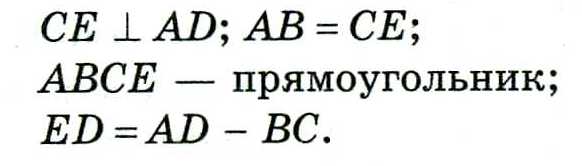
Площадь см. трапеция