Туынды көмегімен теңдеулерді шешу

Сабақтың тақырыбы: Туынды көмегімен теңдеулерді шешу.

Сабақтың мақсаты:

1. Білімділік мақсаты: бағдарламаға сай туынды тақырыбын өткеннен кейін оқушылардың білімдерін кеңейту. Оқушыларды туындының көмегімен теңдеулерді шешуге үйрету;

2. Дамытушылық мақсаты: оқушыларды дамыту мақсатында жұмыс жүргізу, жұмыстану қабілеттерін дамытып, өз бетімен есеп шығаруды үйрету, жаңа материалды меңгеруде қажетті білім, білік, іскерлік дағдыларын қалыптастыру;

3. Тәрбиелік мақсаты: жаңа материалды түсіндіре отырып, отанға, өз ұлтына деген сүйіспеншілікке, жоғары адамгершілік қасиеттеріне тәрбиелеу, болашақта жақсы тұлға болып қалыптасуына жағдай жасау;

Сабақтың түрі: қайталау қосымша сабақ.

Сабақтың әдісі: кітаппен, интерактивті тақтамен жұмыс.

Сабақтың барысы:

1. Ұйымдастыру кезеңі: а) оқушылармен амандасу;

ә) сабаққа дайындау;

б) оқушыларды түгендеу;

в) кезекшімен жұмыс;

г) назарын, зейінін сабаққа аудару;

2. Негізгі бөлім: сабақты түсіндіру кезеңі.

1-мысал:

Шешуі: берілген теңдеуді былайша жазайық:

Ізделінді түбірлер - және g функциялары графиктерінің жанасу немесе қиылысу нүктелерінің абсциссалары. Бұл графиктердің өзара қалай орналасқандығын анықтау үшін олардың экстремумдарын табайық:

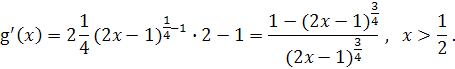
Сондықтан

Бұдан g функциясының аралығында үзіліссіз екенін ескерсек, оның блғанда өсетінін, ал болғанда кемитіндігін түсінеміз. Яғни, g-тің ең үлкен мәні болғанда қабылданады: g.

Сонымен кез келген үшін Демек, берілген теңдеуіміздің жалғыз ғана шешімі бар: .

2-мысал.

Шешуі: Түрлендірулер арқылы теңдеуді мына түрге келтіреміз:

Онда теңдеудің түбірі болатындығын оңай байқауға болады. Басқа түбірлерінің болуы мүмкін емес екенін дәлелдейік.

функция кемімелі болғандықтан, функциясының теңдеудің анықталу облысында, яғни аралығында өсетіндігін көрсетсек жеткілікті.

Туынды табайық:

Егер болса, онда яғни функциясы -да өспелі. Демек, теңдеудің жалғыз түбірі.

3-мысал. -ның қандай мәндерінде теңдеуінің шешімі бар болады?

Шешуі: Теңдеудің анықталу облысында, яғни [2; 4] аралығында функциясын қарастырайық.

Барлық үшін: яғни функциясының максимум нүктесі болатын жалғыз ғана күдікті нүкте. болғандықтан, үзіліссіз.

Демек, Е.

Олай болса, берілген теңдеудің шешімі шарты орындалғанда ғана бар болады.

4-мысал.

Шешуі: көпмүшелігін қарастырамыз.

және көпмүшеліктерінің ең үлкен ортақ бөлгіші болатын g-ті табайық:

Яғни, g (тұрақтыға дейінгі дәлдікпен).

gең үлкен ортақ бөлгіштің жай түбірі.

саны берілген теңдеудің екі еселі түбірі.

Демек, көпмүшелігі -на қалдықсыз бөлінеді.

Сонымен теңдеудің шешімдері:

3. Үйге тапсырма беру.

4. Қорытындылау кезеңі: Оқушылардың жаңа сабақтан алған білімдерін сұрақ қою арқылы анықтау.

5. Бағалау кезеңі.