- Учителю
- Урок по теме: «Действия с обыкновенными дробями» 5 класс.
Урок по теме: «Действия с обыкновенными дробями» 5 класс.
Урок по теме: «Действия с обыкновенными дробями» 5 класс.
Цель урока: обобщение и систематизация знаний об обыкновенных дробях, закрепление и усовершенствование навыков действий с обыкновенными дробями.
Задачи:
-
образовательная: активизировать приобретенные знания об обыкновенных дробях;
-
развивающая: развить элементы творческой деятельности - внимание, зрительную память, речь, смекалку, умение анализировать свои ошибки;
-
воспитательная: прививать интерес к изучению предмета, воспитывать дисциплинированность, честность.
Формы применяемые на уроке:
-
Индивидуальная
-
Фронтальная с использованием ИКТ.
Методы используемые на уроке:
-
Беседа;
-
Игра - «Путешествие»
Оборудование: Компьютер, мультимедийный проектор.
Ход урока:
Организационный момент.
Загадка Она бывает охотничья, барабанная и математическая. (дробь)
Слово учителя:
Мы заканчиваем изучение темы действия с обыкновенными дробями, эта тема в курсе математики занимает одно из первых мест, так как на протяжении всей своей жизни мы постоянно сталкиваемся с дробями. Сегодня на уроке мы должны повторить тему дроби и все действия с обыкновенными дробями. Сегодняшний урок - это урок путешествия по различным станциям, поэтому я желаю вам успеха в преодолении всех трудностей.
Актуализация знаний:
1 станция. «Вопрос - ответ»
-
Как называется деление числителя и знаменателя на одно и то же число? (Сокращение)
-
Как называется элемент дроби, стоящий над чертой, под чертой. (Числитель, знаменатель.)
-
Каким действием можно заменить дробную черту. (Делением)
-
Какие числа называются взаимно обратными.(Произведение которых равно 1)
-
Какая дробь называется правильной, не правильной.
2 станция. «Третий лишний»
Выбери лишнее, объясни почему.
-
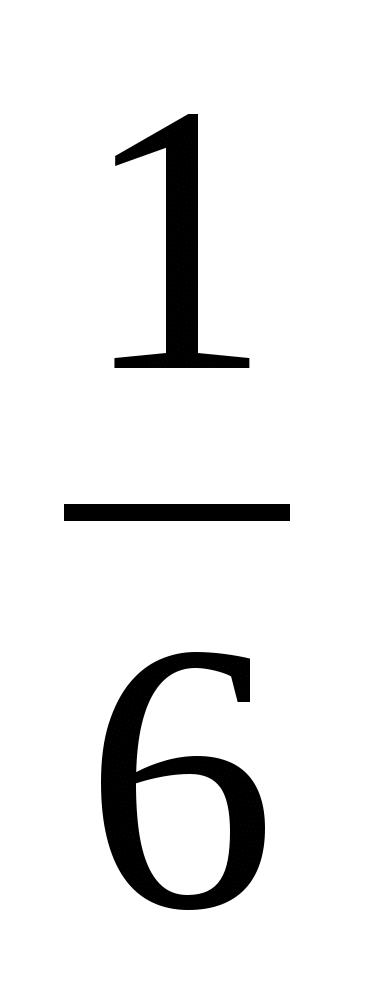 ;
;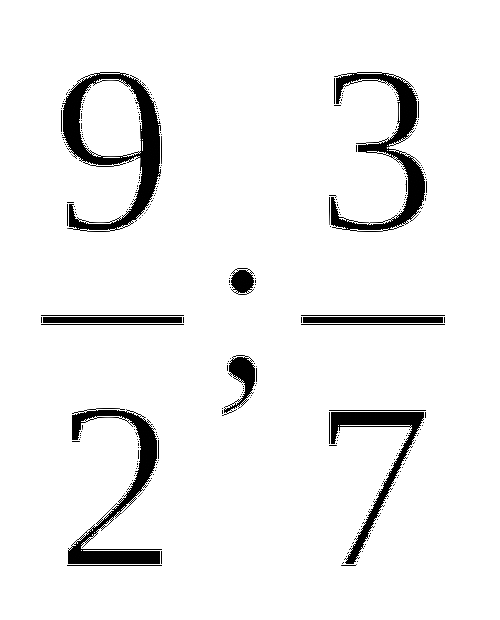 лишняя 9/6 т.к она неправильная.
лишняя 9/6 т.к она неправильная. -
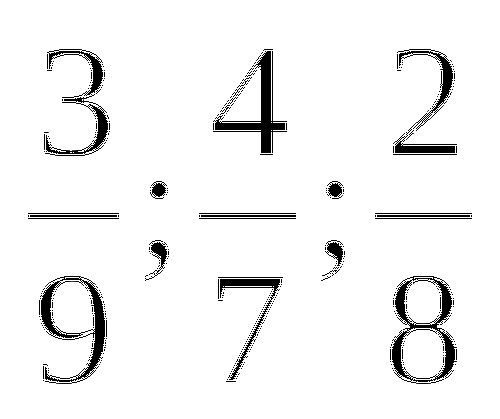 лишняя 4/7 т.к она несократима.
лишняя 4/7 т.к она несократима. -
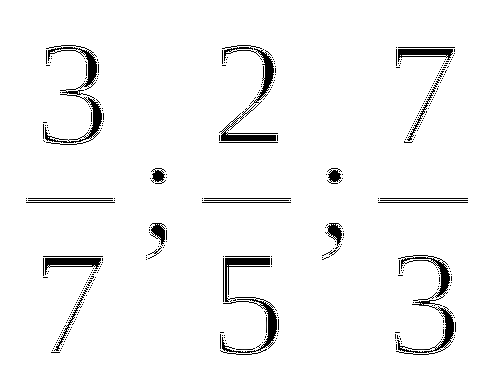 лишняя 2/5 т.к 3/7 и 7/3 взаимообратные.
лишняя 2/5 т.к 3/7 и 7/3 взаимообратные. -
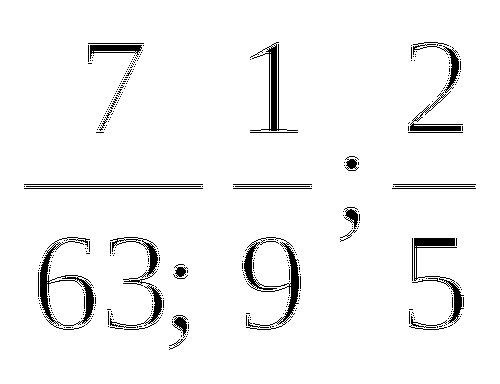 лишняя 2/5 т.к 7/63 и 1/9 это равные дроби.
лишняя 2/5 т.к 7/63 и 1/9 это равные дроби.
3 станция «Историческая
(Домашнее задание доклад)
Дроби появились в глубокой древности. При разделе добычи, при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести дроби. В связи с этой необходимой работой люди стали употреблять выражения: половина, треть, два с половиной шага. Откуда можно было сделать вывод, что дробные числа возникли как результат измерения величин.
Д![]()
![]() ревние египтяне уже знали, как поделить 2 предмета на троих, для этого числа -2/3- у них был специальный значок. Между прочим, это была единственная дробь в обиходе египетских писцов, у которой в числителе не стояла единица - все остальные дроби непременно имели в числителе единицу (так называемые основные дроби): 1/2; 1/3; 1/28. Если египтянину нужно было использовать другие дроби, он представлял их в виде суммы основных дробей.
ревние египтяне уже знали, как поделить 2 предмета на троих, для этого числа -2/3- у них был специальный значок. Между прочим, это была единственная дробь в обиходе египетских писцов, у которой в числителе не стояла единица - все остальные дроби непременно имели в числителе единицу (так называемые основные дроби): 1/2; 1/3; 1/28. Если египтянину нужно было использовать другие дроби, он представлял их в виде суммы основных дробей.
Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.
В![]()
2
1
3начале в записи дробей не использовалась дробная черта, например число записывалось так .
Черта дроби появилась лишь только в 1202 году у итальянского математика Леонардо Пизанского. Он ввел слово дробь. Названия числитель и знаменатель ввел в 13 веке Максим Плануд - греческий монах, ученый, математик.
Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. А записывать дроби как сейчас стали арабы.
В русских рукописных арифметиках XVII века дроби называли долями, позднее «ломаными числами».
Так как мы находимся на станции историческая, то я предлагаю решить старинную задачу Леонтия Филипповича Магницкого - автора знаменитого учебника «Арифметика» 1703г.
Некто спросил учителя: «Сколько у тебя в классе учеников, так как хочу отдать тебе в ученики своего сына?» Учитель ответил: «Если придет еще учеников столько же, сколько имею, и полстолька, и четвертая часть, и твой сын, то тогда у меня будет 100 учеников» Сколько учеников было в классе?
( х+х+1/2х +1/4х+1=100 ответ 36 учеников)
Станция « Ты мне - я тебе»
На доске записаны примеры. Среди них есть верные, есть неверные. Ваша ![]() задача - с помощью символов нарисовать диаграмму по следующему правилу: если пример верный ^, если неверный -. В результате у вас должна получиться определенная геометрическая фигура. Приступим к выполнению задания.
задача - с помощью символов нарисовать диаграмму по следующему правилу: если пример верный ^, если неверный -. В результате у вас должна получиться определенная геометрическая фигура. Приступим к выполнению задания.
На выполнение задания отводится 10 минут.
-
4
 +3
+3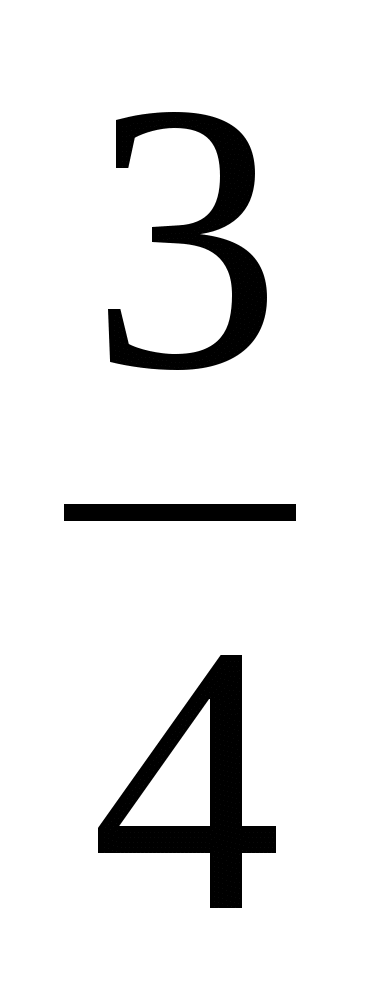 =7
=7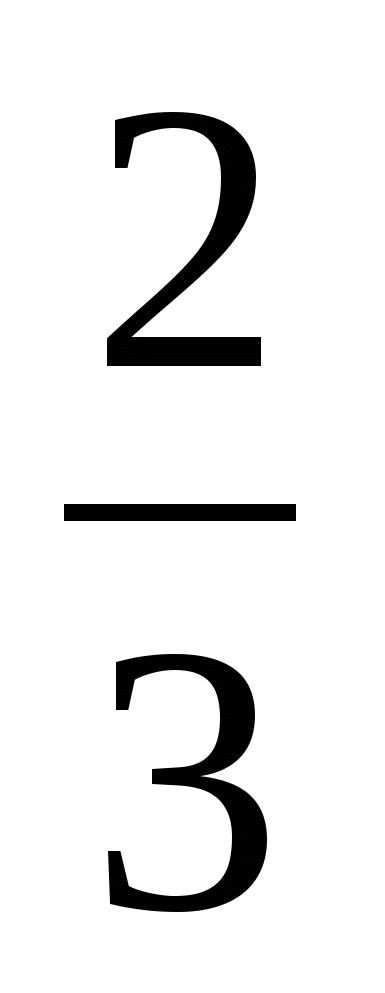
-
7
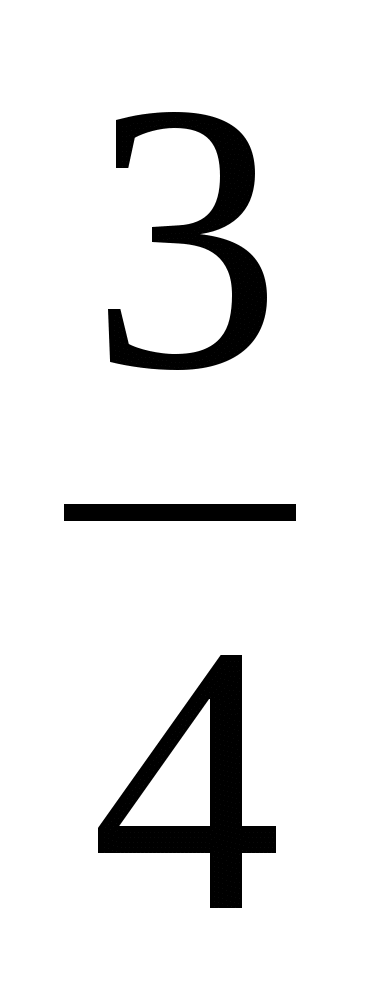 *3=23
*3=23 -
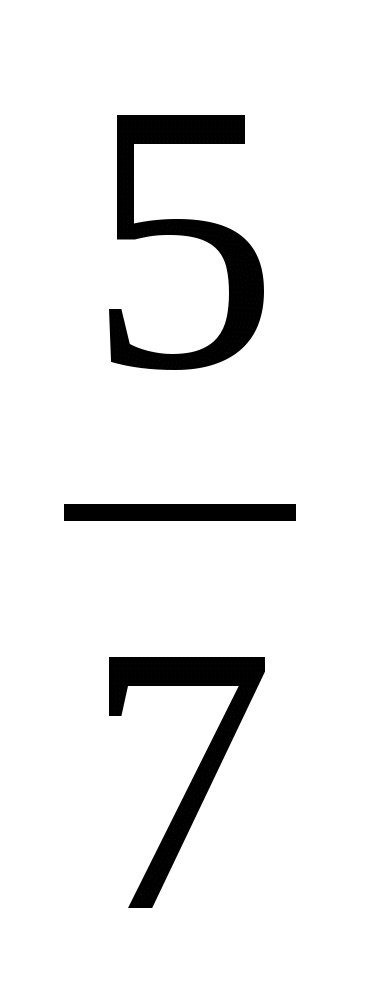
-
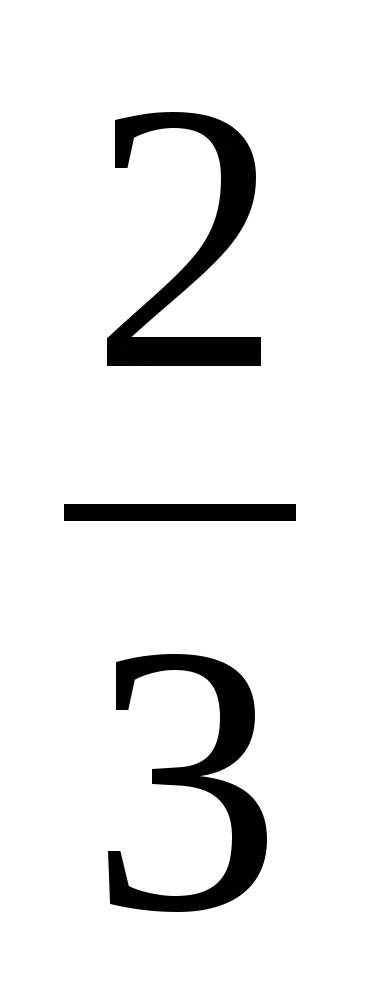 от150=5000
от150=5000 -
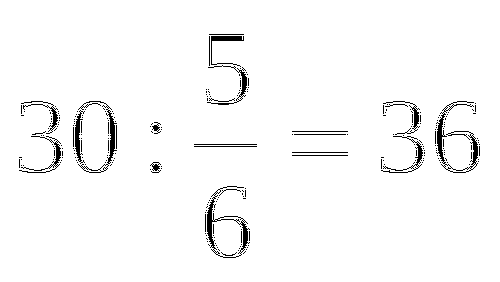
Поменяйтесь тетрадями с соседом и сверьте свои ответы с верным ответом на доске.
-^^-^-^^-^
Критерии выставления оценок:
За все правильные ответы - «5»,
две ошибки - «4»,
три - четыре ошибки «3»,
более четырех ошибок - «2».
После выполнения работы обсудить с учащимися результаты выполнения:
-Что сделано неверно и в каких примерах?
-Какие сложности при выполнении вы испытывали?
Станция задач.
Задача №1. Могла ли одна девочка съесть 2/3 торта, а другая 3/4 этого же торта?
(нет не могла)
Задача №2. Раздели 5 одинаковых яблок между восемью мальчиками поровну. Сделай это с наименьшим числом разрезов.
Задача №3. Определи количество учеников в классе, если 3/8 всех учеников увлекаются математикой, 1/8 историей, 2/8 географией, а остальные 7 человек - биологией (Ответ: 28 человек)
Станция «Итоговая»
Подведение итогов.
Заключительное слово учителя:
Вот и закончилось наше путешествие. Я надеюсь, что сегодняшний урок был для вас интересен и поучителен. да, путь познания нелегок, но знаем мы со школьных лет: загадок больше, чем разгадок и поискам предела нет. ребята, наше путешествие подошло к концу. успехов вам в изучении трудной, но очень интересной науке, которая зовется математикой.
А закончить урок хочется словами великого писателя Л.Н.Толстого.
"Человек подобен дроби: в знаменателе - то, что он о себе думает, в числителе - то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь".