Методическая разработка Организация обратного учебного диалога на уроках математики

Учебный диалог как форма реализации проблемного обучения

Ключевой единицей взаимодействия учителя и учеников в технологии проблемного обучения выступает диалог. Сейчас проблемная технология уже привычная практика для многих учителей. Результатом ее применения становится то, что учащиеся с успехом видят проблему, формулируют ее, даже выдвигают гипотезы. Однако когда дело доходит до поиска плана решения проблем, то на этом этапе возникает большая трудность. И тогда диалог превращается в беседу: учитель спрашивает, ученик отвечает. Решить проблему организации учебного диалога можно. Я передаю инициативу в познании нового ученикам, как бы меняюсь с ними ролью. Ведь чтобы научить ученика задавать вопросы, причем системно, надо ему показать, как это делать.

Тема урока. Первый признак параллельности двух прямых.

Класс. 7

Тип урока. Урок открытия нового знания.

Форма организации учебной деятельности: обратный учебный диалог.

Цель: создать педагогические условия, при которых будут решаться следующие задачи:

- предметные: учащиеся смогут овладеть новыми понятиями - секущая прямая, накрест лежащие углы, частный случай параллельности; сформулировать первый признак параллельности двух прямых; сформулировать общий прием решения задач на параллельность.

- метапредметные: учащиеся смогут последовательно формулировать вопросы в учебном диалоге, сотрудничать в группе, переходить от частного случая к общему.

- личностные: учащиеся смогут убедиться в практической необходимости приобретенного знания.

Структура урока:

1. Организация урока. 1 мин.

2. Этап актуализации субъективного опыта учащихся. 5-7 мин

3. Этап целеполагания. 3-5 мин

4. Этап формирования новых знаний и способов действий. 20-25 мин

5. Этап рефлексии. 3-5 мин

6. Постановка домашнего задания. 1 мин.

Ход урока

I. Организация урока. Задача: сообщение учащимся формы проведения урока.

Учитель: Нам предстоит сегодня искать ответы на многие вопросы. Обычно на уроке учитель спрашивает, а ученик отвечает. Мы попробуем работать наоборот: вы - будете задавать вопросы, я - на них давать ответы. Как вы думаете, надо ли человеку уметь задавать вопросы? Зачем? Уметь задавать вопросы - не просто, поэтому у вас на столах будут специальные карточки - подсказки (Приложение). С их помощью вы будете составлять вопросы.

Далее учителю следует показать на примере одной из карточек, как грамотно составить вопрос.

II. Этап актуализации субъективного опыта учащихся. Задача: актуализация субъективного опыта учащихся о параллельности прямых, постановка проблемного вопроса, формулирование темы урока.

1. Выясняется взаимное расположение прямых на рисунке 1. Здесь уместно вспомнить определение параллельных прямых, знакомое учащимся из курса математики 5-6 классов.

Рисунок 1.

2. Предлагается учащимся сделать рисунок 1 в тетради, на каждой прямой изобразить штриховку, как показано на рисунке 2, и обсудить, параллельны ли теперь те же прямые. Вывод, к которому должны прийти учащиеся может быть таким: на данный момент точно сказать о том, что прямые параллельны мы не можем.

Рисунок 2.

3. Формулируется учащимися проблемный вопрос: «Как определить параллельность прямых?»

4. Далее учащиеся с помощью карточки 1 формулируют тему урока.

Работа с карточкой.

Учитель: Задайте из этой карточки вопрос под номером 1.

Учащиеся: Что показывает приведенный пример?

Ответ учителя:. Приведенный пример показывает, что знать только определение параллельных прямых для ответа на главный вопрос недостаточно.

Учитель: Попытайтесь найти второй вопрос.

Учащиеся: Что надо знать дополнительно?

Ответ учителя: Дополнительно надо знать признаки параллельности двух прямых.

Учитель: Найдите и задайте 3 вопрос.

Учащиеся: Что же мы будем изучать?

Ответ учителя: Мы будем изучать признаки параллельности двух прямых.

Учащимся предлагается сформулировать тему «Признаки параллельности прямых». Тема уточняется и записывается в тетрадь: «Первый признак параллельности двух прямых».

III. Этап целеполагания. Задача: формулирование целей урока.

Учитель организовывает работу в группах по выполнению этой задачи. Для этого учащиеся используют карточку 2.

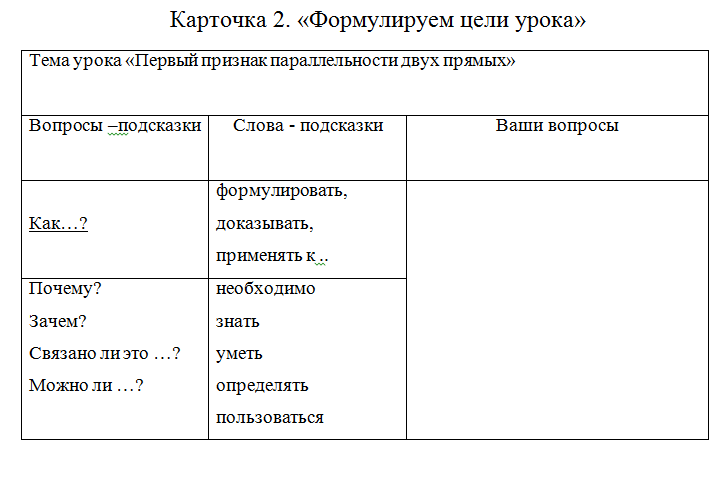
Задание к карточке: «Составьте не менее 3 вопросов к теме нашего урока».

Представление результатов деятельности учащихся по типу «снежный ком» и формулирование ими целей урока (учебных и личностных):

- узнать, как формулируется первый признак параллельности двух прямых, ак доказывается, как применяется для решения задач;

- узнать, люди каких профессий используют эти знания, пригодятся ли знания самим учащимся.

IV. Этап формирования знаний и способ действий. Задача: открытие формулировки первого признака параллельности на основе частного случая, усвоение его доказательства, формулирование общего приема, применяемого при решении задач на доказательство параллельности прямых.

1). Открытие формулировки.

Учащимся предлагается карточка 3.

Задание к карточке. «К каждому новому понятию составьте вопрос».

Работа в группах.

Далее учитель выслушивает вопрос, определяет, корректен ли он, задан ли в определенной последовательности (в противном случае вопрос отклоняется совсем, либо на время, корректируется формулировка) и отвечает. Таким образом, изучаются новые понятия темы.

Ученик: Какая прямая называется секущей?

Ответ учителя. Прямая называется секущей по отношению к двум другим прямым, если она их пересекает в двух точках (ситуация изображается на доске).

Ученик: Какие углы называются накрест лежащими?

Ответ учителя. (используется тот же рисунок). В этом случае образуется 8 углов (нумерация углов на рисунке). Углы …. называются накрест лежащими (показ накрест лежащих углов на рисунке).

Ученик. Какая связь существует между параллельностью и перпендикулярностью прямых?

Ответ учителя. Связь между параллельностью и перпендикулярностью описана и доказана в п.12 на странице 23 учебника (Л.С. Атанасян, «Геометрия 7-9»). Откройте и найдите, как этот факт формулируется. Учащиеся данный факт находят, зачитывают.

«Две прямые, перпендикулярные к третьей прямой не пересекаются, то есть параллельны» (рисунок 3)

Рисунок 3.

Ученик. Что такое частный случай параллельности прямых?

Ответ учителя. Во-первых, частный случай - это один из всевозможных, о котором нам известно. Вот этот случай можно считать частным. Он нам известен и им можно в дальнейшем воспользоваться.

Ученик. Есть ли другие случаи?

Ответ учителя. В других случаях секущая прямая не перпендикулярна к двум прямым, прямые параллельны.

Ученик. Как частный случай может помочь при формулировании первого признака?

Ответ учителя. Постараемся сформулировать первый признак параллельности прямых для частного случая и перенесем его для общего.

Ученик. Как сформулировать первый признак для частного случая?

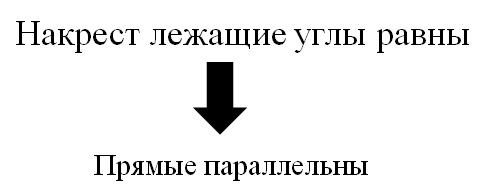
Ответ учителя. Имеем: равные накрест лежащие прямые, и в этом случае прямые параллельны. Попробуйте сформулировать признак параллельности прямых по конструкции: «Если накрест лежащие углы ………………, то …………………………».

Далее формулируется первый признак для общего случая.

Попробуйте сформулировать предложения по такой конструкции. Выслушивается ответ. Согласны ли с таким ответом? Представляется образец - формулировка из учебника п. 25. Выясняется, совпало ли формулировка, данная учащимися с образцом.

Учитель: Поздравляю, вы для себя открыли первый признак параллельности прямых.

2) Доказательство признака.

Учитель: Для общего случая первый признак параллельности надо доказать. Доказательство учитель проводит сам.

Фронтальная работа: выделение условия и заключения теоремы, построение чертежа, запись дано.

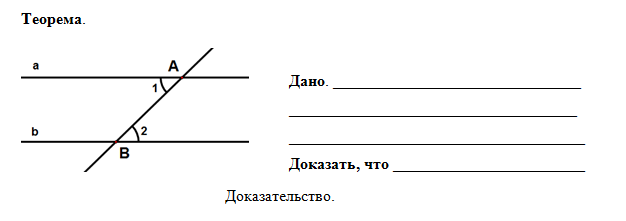
Перед прослушиванием доказательства учащиеся должны получить задание на выявление идеи доказательства. В соответствии с учебником учителем проводится доказательство.

Идея доказательства обсуждается в группах. Результаты групп представляются, совместно вырабатывается идея: «Если углы 1 и 2 прямые, то параллельность прямых в этом случае доказана в пункте 12. Если углы - не прямые, то надо попытаться свести доказательство к случаю 1». Фронтально обсуждается вопрос о порядке выполнения дополнительных построений. Учащиеся при этом используют учебник.

Доказательство теоремы, выражающей первый признак параллельности двух прямых, может быть записано в виде опорного конспекта с пропусками (учет индивидуальных возможностей). Количество пропусков зависит от того, как ученик ориентируется в материале. Ученик должен заполнить пустые места в доказательстве. При этом он может использовать учебник. Работа ведется индивидуально, учитель следит за действиями учеников и оказывает им необходимую помощь. Помощь могут оказывать более сильные учащиеся в группе.

Затем следует проверить двух учеников, предложив им доказать теорему у доски.

Опорный конспект 1.

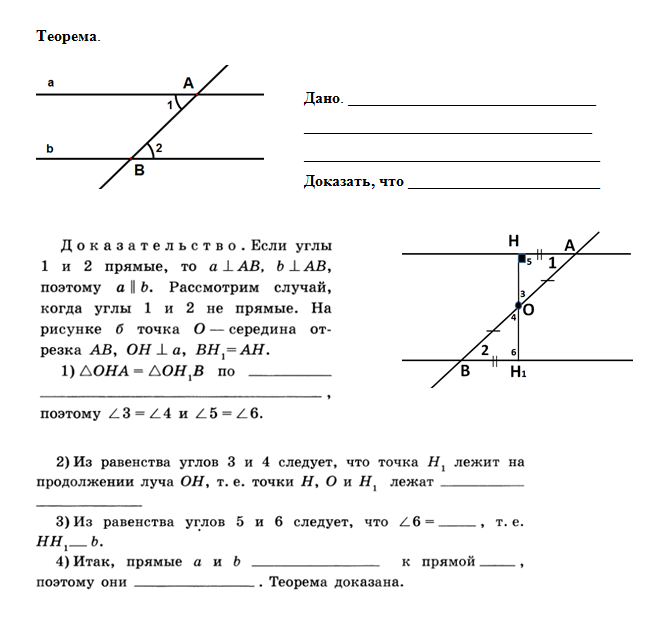
Опорный конспект 2.

3) Формулирование приема, используемого для решения задач.

4) Возврат к исследуемому вопросу.

На этом этапе надо дать ответ на проблемный вопрос, поставленный в начале урока: «Параллельны ли прямые на рисунке?».

</ Учащиеся догадываются провести секущую и использовать прием, сформулированный на предыдущем этапе. Установить равенство углов можно с помощью транспортира. Здесь учитель может познакомить учащихся с инструментами, которые люди для этих целей используют: малкой, рейсхшиной, объяснить, что лежит в основе того или иного инструмента. Можно предложить учащимся воспользоваться одним из них, например, малкой.

V. Итог урока. Рефлексия.

Домашнее задание: п.25 уметь доказывать теорему, выражающую первый признак параллельности двух прямых (для подготовки можно использовать опорный конспект)

На этом этапе приводятся примеры параллельных прямых, которые встречаются в окружающем мире, обсуждается, необходимо ли знать вообще признаки параллельности, достигли ли учащиеся поставленных целей, какие трудности возникли при работе в группах, как этого в дальнейшем можно избежать.

Следующий урок проводится по теме: «Решение задач на применение первого признака параллельности двух прямых».

Литература для подготовки к уроку.

1. А.Д. Король. Как подготовить и провести урок-диалог. Статья. Журнал «Школьные технологии», № 2. 2003 г.

2. А.Д. Король. Как подготовить и провести урок-диалог. Статья. Журнал «Школьные технологии», № 3. 2003 г.