- Учителю
- Конспект урока по математике в 9 классе
Конспект урока по математике в 9 классе
Лопаткина Л.В., учитель математики
МОУ СОШ р.п.Турки Туковского района Саратовской области
Урок математики в 9 классе "Решение рациональных неравенств методом интервалов"
Цели урока:
- формирование умений школьников по решению рациональных неравенств методом интервалов;
- развитие интереса к математике, самостоятельности в приобретении новых знаний;
Оборудование:
Компьютер, мультимедийное оборудование, презентация к уроку.
Ход урока:
I. Организационный момент.
Добрый день, ребята. Сегодня на уроке мы с вами рассмотрим и решим рациональные неравенства методом интервалов. С такими задачами вы встретитесь на ОГЭ.
2.Актуализация знаний. Устно:
1) Является ли данное число а решением данного неравенства
2-6х<-10; а=-2; а=4;
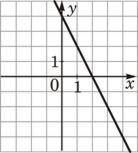
2) На рисунке изображен график функции у=х2+4x+3.
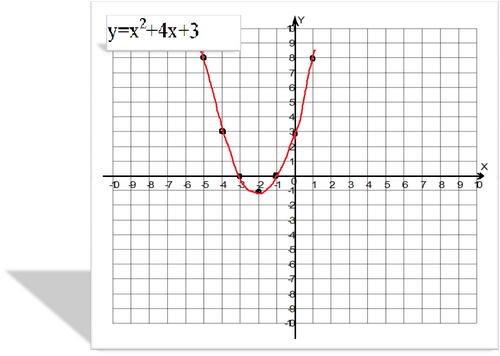
Используя график, решите неравенство х2+4x+3 >0
3) Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) y=− 2x+4 Б) y=2x−4 В) y=2x+4
ГРАФИКИ
1)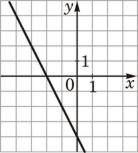 2)
2) 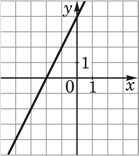 3)
3) 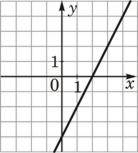 4)
4)
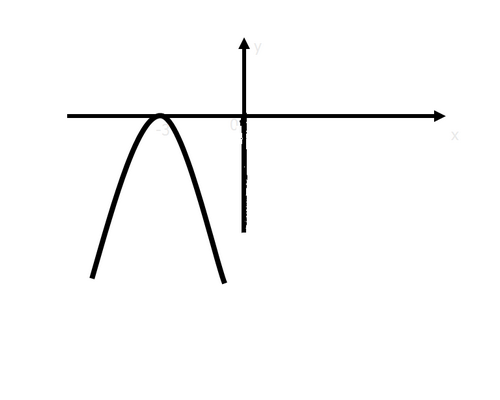
4) Определите на рисунках:
а) область определения, область значений функции;
б) промежутки на которых функция принимает положительные значения, промежутки на которых функция принимает отрицательные значения;
в) наименьшее или наибольшее значение функции, нули функции.
А) Б)
3.Изучение нового материала.
Решить неравенство:(х+2)(х+4)(х-1)<0
f(х)=(х+2)(х+4)(х-1)
х=-2; х=-4; х=1
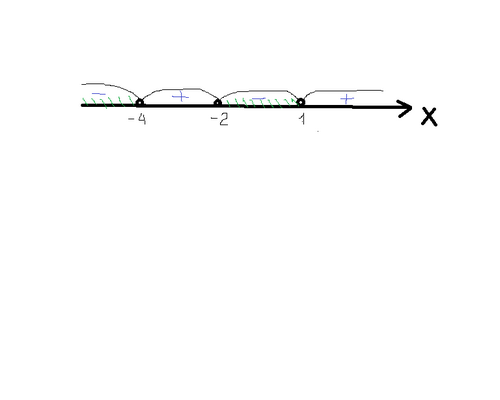 Ответ:(-∞;-4)(-2;1)
Ответ:(-∞;-4)(-2;1)
Вопрос: Что называется областью определения выражения?
y=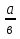 , в
, в 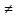 0 y=
0 y=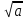 , а
, а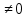
Решить неравенства:1) 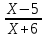 <0
<0
Решение: Неравенство равносильно: (х-5)(х+6)<0
-
 Рассмотрим функцию f(х)=(х-5)(х+6)
Рассмотрим функцию f(х)=(х-5)(х+6) -
Нули функции х=5, х=-6
Ответ:(-6;5)
2)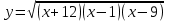 . Решение: (х+12)(х-1)(х-9)≥0
. Решение: (х+12)(х-1)(х-9)≥0 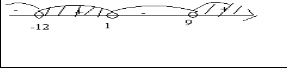 Ответ: [-12;1]È[9;+¥).
Ответ: [-12;1]È[9;+¥).
4.Работа по учебнику
Решить № 2.16.(а,г)
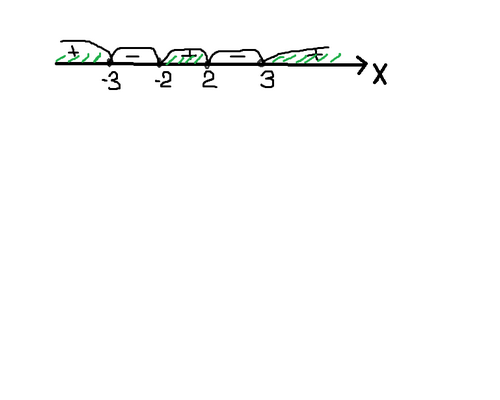
Решение: а)Неравенство (х2-4)/(х2-9)≥0 равносильно:(х2-4)(х2-9)≥0; х=2; х=-2; х=-3; х=3
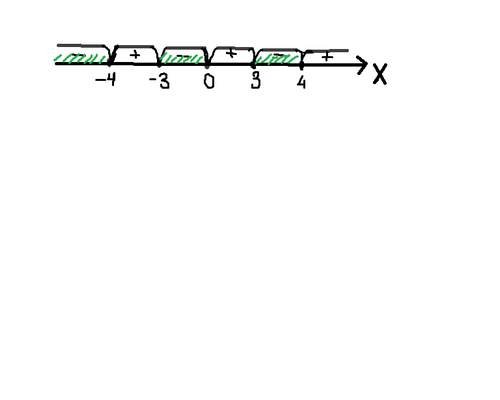
г) Неравенство х(х2-16)/(х2-9)≤0 равносильно х(х-4)(х+4)(х-3)(х+3)≤0
 Ответ: а)(-∞;-3] ᴗ[-2;2] ᴗ[3;∞);
Ответ: а)(-∞;-3] ᴗ[-2;2] ᴗ[3;∞);
г) (-∞;-4]ᴗ [-3;0]ᴗ[3;4]
5.Гимнастика для глаз(2-4 упражнения).
6.Самостоятельная работа.
1.Найти область определения функции:
1 вариант 2 вариант
У=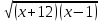 У=
У=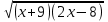
2.Решить неравенство методом интервалов:
1 вариант 2 вариант
а)(х+5)(6-х) ≥ 0; а)(х+6)(х=2 ) < 0;
б)х2 < 196 ; б) х2 ≥ 64х;
в)2х2-9х+4 > 0. в) х2-14х+33 ≤ 0
Итог урока.Д/з п.2, на оценку "3"-№2.20(а,б);2.21(а)
на оцеку "4"-№2.21(б); 2.22(а,б)
на оценку "5"- 2.22(в); 2.31