Урок алгебры. Возрастание и убывание фунуции.

Урок алгебры и начал анализа по теме: «Возрастание и убывание функции».

Учебник «Алгебра и начала анализа» для 10-11 классов общеобразовательных учреждений авторов Ш.А. Алимова, Ю.К. Колягина, Ю.В. Сидорова, Н.Е. Фёдоровой, М.И. Шабунина, вышедший в 2000г.

Ермолина Марина Владимировна, учитель математики, МБОУ «Лицей», г. Черногорск.

Статья отнесена к разделу: Преподавание математики.

Задачи урока:

Образовательная:

• организовать деятельность учащихся по применению достаточных условий возрастания и убывания функции к нахождению промежутков монотонности функции;

Развивающая:

• содействовать развитию памяти, речи, умению обобщать;

Воспитательные:

• формировать логическое, системное мышление;

• формировать ответственность, организованность;

• способствовать укреплению здоровья.

Тип урока: комплексного применения знаний, умений и навыков; проверки и оценки знаний.

Метод: репродуктивный.

Оборудование: карточки с заданиями для проверочной работы, чертёж на доске; материал для минуты отдыха.

План урока:

1. Организационный момент.

2. Устная работа.

3. Проверка домашнего задания.

4. Решение задач по теме урока.

5. Минута отдыха.

6. Проверочная работа.

7. Итог урока.

8. Домашнее задание.

Ход урока:

І. Организационный момент.

Урок начинается со слов Франса А.: «Чтобы переварить знания, надо поглощать их с аппетитом». « Как это получится у нас, узнаем …»

Ребятам сообщается структура урока.

ІІ. Устная работа.

1.Вопросы учащимся:

- какие основные способы задания функции мы знаем?

- дать определение возрастающей функции.

- дать определение убывающей функции.

- сформулируйте достаточное условие возрастания функции.

- сформулируйте достаточное условие убывания функции.

- как по-другому называют промежутки возрастания и убывания функции?

- концы промежутков монотонности включаем в промежутки?

(Замечание: если функция непрерывна в каком-либо из концов промежутка возрастания (убывания), то его можно присоединить к этому промежутку.)

2.Чтение графика. Рассмотреть два случая: а) если это график функции f(x);

б) если это график функции (x);

Указать число промежутков возрастания и убывания.

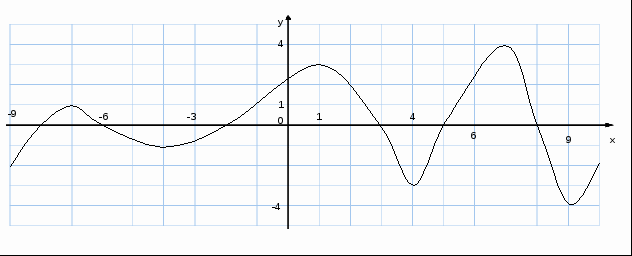
ІІІ. Проверка домашнего задания.

№652(1,2)

Решить неравенства:

1)

2)

(Повторение решения тригонометрических неравенств понадобится при решении №905(1))

№869(2,8)

Найти производную функции:

2) -+2

8)

№872(4,6)

Найти производную функции:

4) хsin2x

6)

( по ходу проверки домашнего задания с ребятами повторяются правила дифференцирования произведения, сложной функции и таблица производных)

№900(4)

Найти промежутки возрастания и убывания функции у=х+12х-100 двумя способами: а) с помощью графика функции; б) с помощью графика производной функции.

ІV. Решение задач.

(прежде, чем приступить к решению задач, необходимо вспомнить с учащимися алгоритм исследования функции на монотонность аналитическим способом)

№900(6,7)

Найти промежутки возрастания и убывания функции:

6) у=х (повторяется метод интервалов)

7) у=2х

№903(4)

Найти промежутки возрастания и убывания функции:

4) у=х

№905(1)

Найти промежутки возрастания и убывания функции х-sin2x

V. Минута отдыха.

Учитель показывает одну за другой карточки с надписями: (sinx), (2х, (log, (8х, (-5х), (3cosx), (7), (lnx), (cosx+2).

По всему классу на карточках развешены варианты ответов, учащимся необходимо выбрать правильный и указать на него рукой.

Будет видно, кто ещё недостаточно знает таблицу производных.

VІ. Проверочная работа.

1 вариант.

1) Найдите производную функции f(x)=3x

2) На рисунке изображён график производной функции у=f, заданной на отрезке . Исследуйте функцию у=f(x) на монотонность и в ответе укажите число промежутков убывания.

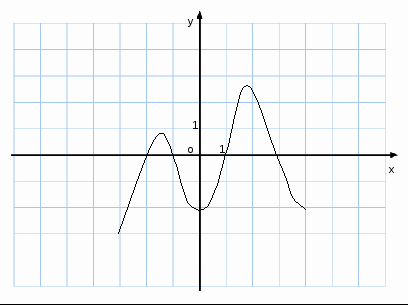
3) Определите промежутки возрастания функции f(x)=x

2 вариант.

1) Найдите производную функции h=4x

2) На рисунке изображён график производной функции у=f, заданной на отрезке . Исследуйте функцию на монотонность и в ответе укажите число промежутков возрастания.

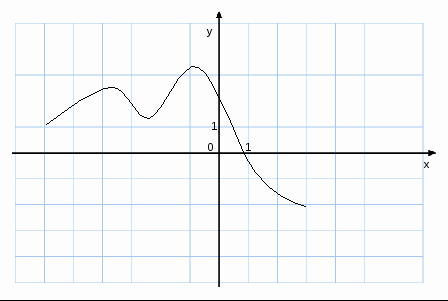
3) Найдите промежутки убывания функции f(x)=x.

3 вариант.

1) Вычислите производную функции у=х

2) На рисунке изображён график производной функции у=f(x), заданной на отрезке . Исследуйте функцию у=f(x) на монотонность и укажите число промежутков убывания.

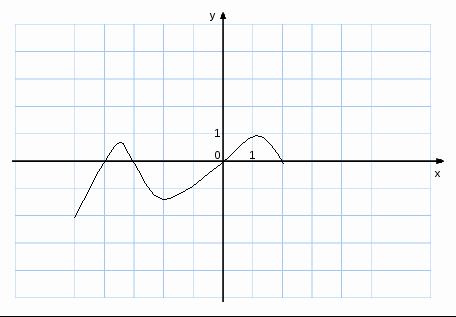
3) Определите промежутки возрастания функции f(x)=x.

4 вариант.

1) Вычислите производную функции y=cosx+x

2) На рисунке изображён график производной функции у=f(x), заданной на отрезке .

Исследуйте функцию у=f(x) на монотонность и в ответе укажите число промежутков возрастания.

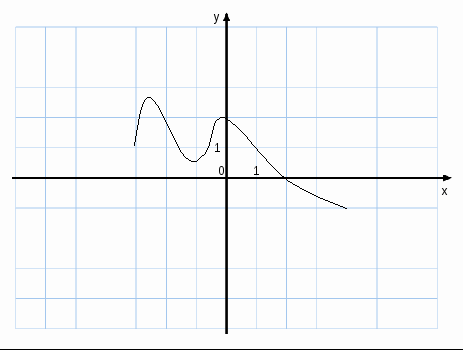
3) Найдите промежутки убывания функции f(x)=x.

5 вариант.

1) Найдите производную функции у=.

2) На рисунке изображён график производной функции у=f, заданной на отрезке .

Исследуйте функцию на монотонность и в ответе укажите число промежутков убывания.

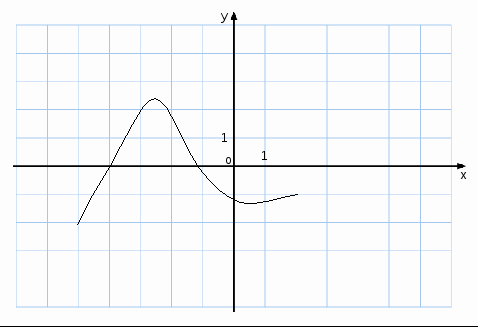
3) Найдите промежутки возрастания функции f(x)=x

6 вариант.

1) Найдите производную функции g(x)=7x.

2) На рисунке изображён график производной функции у=f(x), заданной на отрезке .

Исследуйте функцию у=f(х) на монотонность и в ответе укажите число промежутков возрастания.

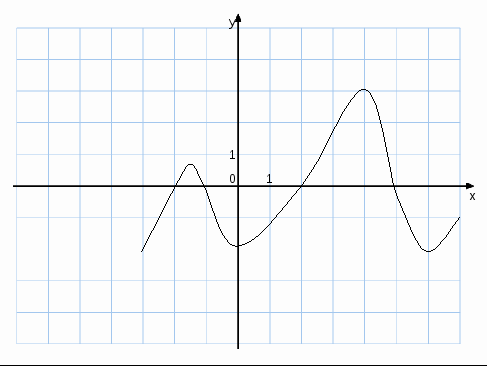
3) Найдите промежутки убывания функции f(х)=х

VІІ. Итог урока. Выставление оценок.

VІІІ. Домашнее задание.

№904

Найти промежутки возрастания и убывания функции.

1) у=; 2) у=3.

№905(2)

Найти промежутки возрастания и убывания функции у=3х+2cos3x.

№908*

При каких значениях а функция у=ах возрастает на всей числовой прямой?

6