План-конспект урока на тему «Параллелепипед» (10, 11 класс)

ПЛАН-КОНСПЕКТ УРОКА

Тема «Параллелепипед»

Цели урока:

• введение определений и свойств параллелепипеда;

• закрепить знание при решении задач обязательного уровня;

• обобщить подходы к решению задач в форме алгоритма.

Обучающие:

• познакомить учащихся с фигурой параллелепипед;

• познакомить со свойствами параллелепипеда;

• сформировать у учащихся умения и навыки решения задач;

• показать на многообразии природных данных связь с окружающим нас миром.

Развивающие:

• развитие математического и общего кругозора, внимания, умений сравнивать, классифицировать, проводить анализ и самоанализ.

Воспитательные:

• развивать внимание, логическое мышление, математическую речь;

• воспитание культуры речи учащихся, усидчивости; прививать учащимся интерес к предмету.

Тип урока: изучение нового материала.

Оборудование: учебник Л. С. Атанасяна «Геометрия 10-11», разработанный дидактический материал.

План урока:

1. Организационный момент

2. Актуализация знаний

3. Изучение нового материала

4. Решение задач

5. Подведение итогов

6. Домашнее задание

Ход урока:

1. Организационный момент

Приветствие учеников, проверка посещаемости, проверка готовности помещения к уроку.

На прошлом уроке мы знакомились с многогранниками, а именно с такой геометрической фигурой, как призма. Сегодня мы начнем изучение новой темы «Параллелепипед», но для начала вспомним определение призмы, ее построение.

2. Актуализация знаний

Что называют призмой?(ученики отвечают)

Расскажите алгоритм построения призмы? (ученики отвечают)

3. Изучение нового материала

Опр. Поверхность, составленная из двух равных параллелограммов ABCD и A₁B₁C₁D₁ и четырех параллелограммов, называется параллелепипедом и обозначается так: ABCDA₁B₁C₁D_1.

Параллелепипед - , основанием которой служит , или (равносильно) многогранник, у которого шесть граней и каждая из них - параллелограмм.

Алгоритм построения параллелепипеда:

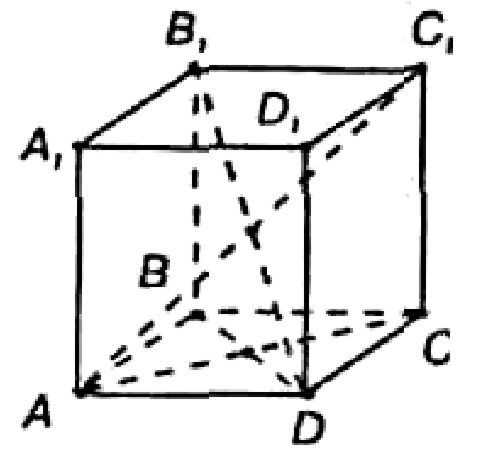
Рассмотрим два равных параллелограмма ABCD и A₁B₁C₁D_{1 ,} расположенных так, что отрезки AA₁, BB_1, CC_1, DD₁ параллельны. Четырехугольники AB B₁A_1, BCC₁B_1, CDD₁C₁ и DA D₁A₁ также являются параллелограммами, т. к. каждый из них имеет попарно параллельные противоположные стороны.

Основные элементы параллелепипеда:

• Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро - смежными.

• Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными.

• , соединяющий противоположные вершины, называется параллелепипеда.

• Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.

Параллелепипед состоит из 6 граней, 12 ребер и 8 вершин.

Назовите их? (Ученики отвечают)

Назовите диагонали параллелепипеда? (Ученики отвечают)

Назовите основания и боковые грани параллелепипеда? (Ученики отвечают)

Свойства параллелепипеда:

• Противоположные грани параллелепипеда равны и попарно параллельны.

• Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

Типы параллелепипедов:

• - это параллелепипед, у которого все грани - .

• Наклонный параллелепипед - это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Прямой параллелепипед

• Площадь боковой поверхности S_б=Р_о*h, где Р_о - периметр основания, h - высота

• Площадь полной поверхности S_п=S_б+2S_о, где S_о - площадь основания

Прямоугольный параллелепипед

• Площадь боковой поверхности S_б=2c(a+b), где a, b - стороны основания, c - боковое ребро прямоугольного параллелепипеда

• Площадь полной поверхности S_п=2(ab+bc+ac)

4. Решение задач

А сейчас переходим к решению задач по теме «Параллелепипед».

Для начала немного поработаем устно. В геометрии есть теорема, с помощью которой мы можем с легкостью вычислить диагонали параллелепипеда: .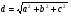

На применение этой теоремы решим задачу.

Ребра и высота прямоугольного параллелепипеда равны 4 см, 4 см и 2 см соответственно. Вычислите диагональ параллелепипеда (устно).

Задача № ____Боковое ребро прямого параллелепипеда 5 м, стороны основания 6 м и 8 м, а одна из диагоналей основания 12м. Найдите диагонали параллелепипеда. (Один ученик выходит к доске, остальные работают в тетрадях)

Дано: Прямой параллелепипед, СС₁=5, AD=8, CD=6, АС=12

Найти: AС₁, В₁D-?

Запись условия и требования задачи

Решение: 1) AС₁²= АС²+ СС₁²

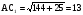м.

Итак, будем искать диагональ AС_1. Из какого треугольника мы ее найдем?

Ученики: Из треугольника AСС_1.

Что в этом треугольнике известно?

Ученики: Известна диагональ основания АС=12, боковое ребро СС₁=5. Также треугольник AСС₁ прямоугольный. По теореме Пифагора найдем AС_1.

Правильно. Записываем формулу и подставляем в нее значения.

2) 2AB² + 2AD² = AC² + ВD²;

ВD²= 2AB² +2AD² - AC²;

Из какого треугольника мы найдем диагональ В₁D?

Ученики: Из треугольника ВВ₁D_.

Что в этом треугольнике известно?

Ученики: Известно только боковое ребро ВВ₁=5.

Что будем искать перед нахождением диагонали?

Ученики: Вторую диагональ основания?

Основание параллелепипеда - параллелограмм ABCD со сторонами АВ=6 м, AD=8 м и диагональю АС=12 м. Так как в параллелограмме сумма квадратов всех сторон равна сумме квадратов диагоналей, то 2AB² + 2AD² = AC² + ВD². Что мы получаем?

Ученики: ВD²= 2AB² +2AD² - AC². Отсюда выразим ВD.

Выражаем.

3) 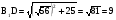м.

Ученики: Теперь зная две стороны прямоугольного треугольника ВВ₁D, можем найти третью по т. Пифагора.

Ответ: 13 м и 9 м

Итак, 13 м и 9 м

5. Подведение итогов

Сегодня на уроке мы познакомились с такой геометрической фигурой, как параллелепипед, рассмотрели основные свойства этой фигуры, алгоритм построения, типы параллелепипедов.

6. Домашнее задание