- Учителю
- Опорный конспект по математике 6 класс
Опорный конспект по математике 6 класс
Опорный конспект для 6 класса (часть 1)
учитель математики МКОУ СОШ №53
Грудовенко Н.П.
г.Миасс, Челябинская область
Компонеты математических действий
Сложение: слагаемое + слагаемое = сумма
Вычитание: уменьшаемое - вычитаемое = разность
Умножение: множитель . множитель = произведение
Деление: делимое : делитель = частное
Делимость чисел
Делителем натурального числа а называют натуральное число, на которое а делится без остатка.
пример: Число 12 имеет шесть делителей: 1, 2, 3, 4, 6 и 12.
Наибольшее натуральное число, на которое делятся без остатка числа а и b, называют наибольшим общим делителем этих чисел. (НОД)
пример: Найдем наибольший общий делитель чисел 24 и 36.
делителями числа 24 будут 1, 2, 3, 4, 6, 8, 12, 24
делителями числа 36 будут 1, 2, 3, 4, 6, 9, 12, 18, 36
Наибольшим среди общих делителей будет число 12. То есть 12 - наибольший общий делитель чисел 24 и 36.
Если НОД чисел равен 1, то такие числа называют взаимно простыми.
Кратным натурального числа а называют натуральное число, которое делится без остатка на а. Любое натуральное число имеет бесконечно много кратных.
пример: Число 12 имеет следующие кратные: 12, 24, 36, 48, 60 и так далее.
Наименьшим общим кратным (НОК) чисел а и b называют наименьшее натуральное число, которое кратно и а, и b.
пример: НОК чисел 75 и 60 будет 300.
Признаки делимости
На 10
На 5
На 2
На 3
На 9
Если число оканчивается цифрой 0
Если число оканчивается цифрой 0 или 5
Если число оканчивается четной цифрой
Если сумма цифр числа делится на 3
Если сумма цифр числа делится на 9
Десятичные дроби
Десятичная дробь - дробь, в которой целая часть отделена от дробной запятой.
Чтобы сложить (вычесть) десятичные дроби, нужно:
1. уравнять в этих дробях количество знаков после запятой
2. записать их друг под другом так, чтобы запятая была под запятой
3. выполнить сложение (вычитание), в ответе оставив запятую под запятой
пример: 1) 3,7 + 2, 651 = 6,351
-
3
,
7
0
0
+
2
,
6
5
1
6
,
3
5
1
2) 3,7 - 2,651 = 1,049
-
3
,
7
0
0
-
2
,
6
5
1
1
,
0
4
9
3) 16,6 - 5,99 = 16,60 - 5,99 = 10,61
-
1
6
,
6
0
-
5
,
9
9
1
0
,
6
1
Чтобы умножить десятичную дробь на натуральное число, надо умножить ее на это число, не обращая внимания на запятую, а в полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби
пример: 1,83 . 4 = 7,32
-
1
,
8
3
х
4
7
,
3
2
Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.
пример: 1) 0,065 . 1000 = 0065 = 65
→
2) 2,9 . 100 = 290
→
Чтобы разделить дробь на натуральное число, надо разделить эту дробь на число, не обращая внимания на запятую, поставить в частном запятую, когда закончится деление целой части.
Если целая часть меньше делителя, то частное начинается с нуля.
пример: 2,88 : 4 = 0,72
-
2,
8
8
4
0
0,
7
2
2
8
2
8
8
8
0
Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе. При этом, иногда, приходится написать перед целой частью нуль или несколько нулей.
пример: 1) 96,1 : 10 = 9,61
←
2) 8,765 : 100 = 008,765 : 100 = 0,08765
←
Чтобы перемножить две десятичные дроби, надо выполнить умножение, не обращая внимание на запятые, в полученном произведении отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.
Если в произведении получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей.
пример: 1) 1,8 . 0,6 = 1,08
-
1,
8
х
0,
6
1,
0
8
2) 0,254 . 0,03 = 0,00762
-
0,
2
5
4
х
0,
0
3
0,
0
0
7
6
2
Чтобы разделить число на десятичную дробь, надо в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе, после этого выполнить деление на натуральное число.
пример: 12,096 : 2, 24 = 1209,6 : 224 = 5,4
→ →
-
1
2
0
9,
6
2
2
4
1
1
2
0
5,
4
8
9
6
8
9
6
0
Проценты
Процентом называют одну сотую часть числа.
Так как 1% равен сотой части величины, то вся величина равна 100%
Чтобы представить % в виде десятичной дроби, надо % разделить на 100.
пример: 1% = 1 : 100 = 0,01
6% = 6: 100 = 0,06
45% = 45: 100 = 0,45
315% = 315: 100 = 3,15
Чтобы записать десятичную дробь в виде %, надо дробь умножить на 100.
пример: 0,87 . 100% = 87%
0,07 . 100% = 7%
Обыкновенные дроби.
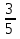 - обыкновенная дробь, 3 - числитель дроби, 5 - знаменатель дроби
- обыкновенная дробь, 3 - числитель дроби, 5 - знаменатель дроби
Если числитель дроби меньше ее знаменателя, то дробь называется правильной, ( 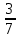 )
)
Если числитель дроби больше ее знаменателя, то дробь называется неправильной ( 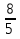 )
)
Чтобы из неправильной дроби выделить целую часть, надо:
1. разделить числитель на знаменатель (с остатком)
2. неполное частное будет целой частью
3. остаток дает числитель, а знаменатель не меняется
пример: 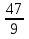 . Разделим 47 на 9 (47 : 9 = 5 остаток 2), значит
. Разделим 47 на 9 (47 : 9 = 5 остаток 2), значит 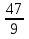 = 5
= 5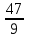
Чтобы смешанное число представить в виде неправильной дроби, надо:
1. умножить его целую часть на знаменатель дробной части
2. к полученному произведению прибавить числитель дробной части
3. записать полученную сумму числителем дроби, а знаменатель оставить без изменений.
пример: 3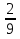 =
= 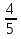 (3 . 5 = 15, 15 + 4 = 19 - это новый числитель)
(3 . 5 = 15, 15 + 4 = 19 - это новый числитель)
Действия с дробями с одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями, числители складывают, а знаменатель оставляют тот же.
пример: 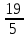 +
+ 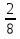 =
= 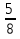 =
= 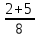
При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же.
пример: 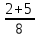 -
- 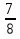 =
= 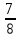 =
= 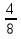
При сложении смешанных чисел отдельно складывают целые части, отдельно дробные.
пример: 3 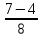 + 2
+ 2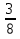 = 5
= 5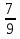 = 6
= 6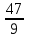 (3+2=5,
(3+2=5, 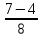 +
+ 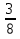 =
= 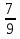 - неправильная дробь, запишем в виде правильной, выделив целую часть)
- неправильная дробь, запишем в виде правильной, выделив целую часть)
При вычитании смешанных чисел поступают так же, как при сложении
пример: 2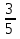 - 1
- 1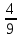 = 1
= 1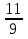 (2-1=1,
(2-1=1, 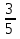 -
- 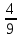 =
= 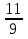 )
)
Если при вычитании смешанных чисел числитель уменьшаемого меньше числителя вычитаемого поступают так: 6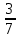 - 2
- 2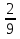 = (5+1
= (5+1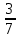 ) - 2
) - 2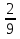 = 5
= 5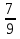 - 2
- 2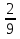 = 3
= 3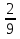
Основное свойство дроби. Если числитель и знаменатель дроби умножить или разделить на одно и тоже число, то получится равная ей дробь.
Сократить дробь - это значит разделить числитель и знаменатель на их общий делитель, отличный от единицы.
пример: 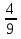 =
= 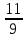 , то есть числитель и знаменатель дроби разделили на их общий делитель 75.
, то есть числитель и знаменатель дроби разделили на их общий делитель 75.
Чтобы сравнить (сложить или вычесть) дроби с разными знаменателями, надо привести данные дроби к наименьшему общему знаменателю.
Чтобы привести дроби к наименьшему общему знаменателю, надо:
1. найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
2.для каждой дроби определить дополнительный множитель, для этого разделить общий знаменатель дробей на знаменатель каждой дроби
3. умножить знаменатель и числитель каждой дроби на ее дополнительный множитель.
пример: 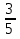 и
и 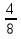
1. НОК чисел 6 и 8 является 24.
2. дополнительный множитель для первой дроби 4 (24 : 6 = 4)
дополнительный множитель для второй дроби 3 (24 : 8 = 3)
3. 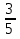 умножим на 4,
умножим на 4, 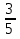 =
= 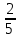 ;
; 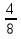 умножим на 3 ,
умножим на 3 , 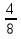 =
= 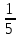
Смешанные числа
Чтобы сложить смешанные числа, надо:
1. привести дробные части этих чисел к наименьшему общему знаменателю;
2. выполнить сложение.
пример: 5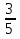 + 3
+ 3 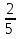 = 5
= 5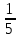 + 3
+ 3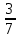 = 8
= 8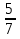 = 9
= 9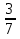 ,
,
сначала привели дроби к общему знаменателю 12, (при этом дополнительный множитель для первой дроби будет 2, дополнительный множитель для второй дроби будет 3), затем сложили целые части (5+3) и дробные части, в результате получили неправильную дробь и выделили из нее целую часть.
Чтобы выполнить вычитание смешанных чисел, надо:
1. привести дробные части этих чисел к наименьшему общему знаменателю;
2. если числитель дроби уменьшаемого меньше числителя дроби вычитаемого, то первую дробь записать в виде неправильной дроби, уменьшив на 1ее целую часть;
3. выполнить вычитание.
пример: 3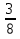 - 1
- 1 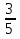 = 3
= 3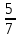 -1
-1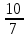 = 2
= 2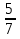 - 1
- 1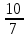 = 1
= 1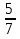 ,
,
сначала привели дроби к общему знаменателю 18, (при этом дополнительный множитель для первой дроби будет 2, дополнительный множитель для второй дроби будет 3), так как при этом получили, что числитель первой дроби меньше числителя второй дроби (8 < 15), то записали первую дробь в виде неправильной 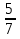 , (при этом целую часть уменьшили на единицу), затем выполнили вычитание целых частей (2 - 1) и дробных частей.
, (при этом целую часть уменьшили на единицу), затем выполнили вычитание целых частей (2 - 1) и дробных частей.
Умножение дробей.
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменений.
пример: 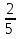 . 5 =
. 5 = 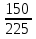 =
= 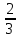 = 3
= 3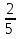
Чтобы умножить дробь на дробь, надо числитель первой дроби умножить на числитель второй дроби, и знаменатель первой дроби умножить на знаменатель второй дроби. При этом выполнить возможные сокращения.
пример: 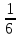 .
. 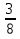 =
= 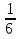 =
= 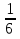 =
= 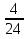
Чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
пример: 9 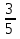 . 1
. 1 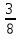 =
= 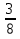 .
. 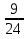 =
= 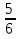 =
= 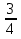 =
= 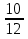 = 13
= 13 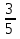
Деление дробей
Чтобы разделить одну дробь на другую, надо делимое умножить на число. обратное делителю.
пример: 1) 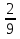 :
: 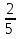 =
= 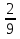 .
. 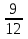 =
= 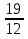
2) 2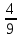 : 1
: 1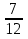 =
= 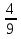 :
: 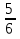 =
= 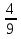 .
. 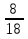 =
= 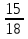 =
= 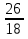 = 2
= 2 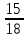
Нахождение дроби от числа
Чтобы найти дробь от числа, нужно умножить число на эту дробь.
пример: 1) Путешественник прошел за два дня 20 километров. В первый день он прошел 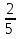 этого расстояния. Сколько километров прошел путешественник в первый день?
этого расстояния. Сколько километров прошел путешественник в первый день?
решение: 20 . 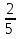 =
= 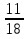 = 15
= 15
2) В городе 550 тыс. жителей. Население в нем ежегодно увеличивается на 3%. Сколько жителей будет в городе через год?
решение: 3% = 0,03. Население города составляет 100%, 100% = 1, значит через год оно будет составлять 1 + 0,03 = 1,03 (то есть 103%). Тогда 550 . 1,03 = 566,5 (тыс. жителей)
Нахождение числа по его дроби
Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.
пример: 1) Пшеницей засеяно 2400 га, что составляет 0,8 всего поля. Найдите площадь всего поля.
решение: 2400 : 0,8 = 24000 : 8 = 3000 (га) - площадь всего поля
2) Масса вяленой рыбы составляет 55% массы свежей рыбы. Сколько нужно взять свежей рыбы, чтобы получить 231 кг вяленой?
решение: Так как 55% = 0,55, то чтобы узнать сколько понадобится свежей рыбы, надо 231 : 0,55 = 23100 : 55 = 420 (кг)
9