Исследовательская работа по математике на тему Числа-великаны (6 класс)

Введение

Две стихии господствуют в математике - числа и фигуры с их бесконечным многообразием свойств и взаимосвязей. Само возникновение понятия числа - одно из гениальнейших проявлений человеческого разума. Действительно, числами не только что-то измеряют, ими сравнивают, вычисляют, даже рисуют, проектируют, сочиняют, играют, делают умозаключения, выводы. Когда- то числа служили только для решения практических задач. А потом их стали изучать, узнавать их свойства.

Открытия в науке о числах делали Пифагор, Архимед, немецкий ученый Карл Гаусс, французские математики Алексис Клеро, Эверист Галуа, Шюке и др. Сначала люди умели называть лишь маленькие числа, а потом все больше и больше. Они создали разные системы исчисления, такие как двоичная, десятичная, шестидесятеричная.

Около 2.5- 3 тысяч лет до нашей эры египтяне придумали свою числовую систему. Своя система счисления была у римлян. В древности применялась и алфавитная система записи чисел. Любопытны были различные методы обозначения чисел. Но у всех этих методов был один недостаток: по мере увеличения чисел нужны были все новые и новые знаки.

Впрочем, египтяне, римляне, греки с большими числами в своей практике не встречались. И когда древнегреческий математик Архимед научился называть громадные числа и изложил свое открытие в книге «Псаммит» т.е. «Счет песчинок» никто на это никто не обратил внимание. Человечество развивалось и двигалось вперед. Люди пытались вычислить площадь земли, расстояние от земли до солнца, расстояние между звездами, изучали молекулы, атомы. Появилась необходимость в обозначении больших чисел. Ученые задумались: «Есть ли предел у числового ряда, как назвать и записать большое число?» В жизни мы эти числа почти не встречаем. Только в науке нужны большие числа.

Но изучение чисел и их свойств необходимо современному человеку для развития логического мышления, памяти, творческого решения задач. В школьном курсе «математика» не изучается тема «числа - великаны», но узнав, что существуют числа больше миллиарда, у меня возник интерес и желание больше узнать об этих числах. Безусловно, мало знать, как называются самые большие числа в мире, имеющие собственное название. Интересно узнать и посмотреть на то, как они записываются, где встречаются в жизни.

Это и обусловило выбор темы работы: «Числа - великаны».

План исследований

Актуальность: расширить свой кругозор в употреблении чтения многозначных чисел- великанов в области астрономии, химии, физики.

Объект исследования: удивительный мир чисел

Предмет исследования: числа - великаны

Цель - знакомство с названием чисел - великанов, умение их читать.

Задачи:

1. Узнать об истории возникновения чисел, различных систем счисления.

2. Изучить необходимый теоретический материал.

3. Уточнить название классов для дальнейшего чтения чисел- великанов.

4. Уметь применять эти числа при решении задач и в других предметных областях.

Гипотеза: Если узнаем историю возникновения чисел, системы счисления и название классов, тогда легко будем читать и писать большие числа. Сможем избежать трудностей при чтении, сталкиваясь на практике с числами- великанами.

Основная часть

1. Появление названия чисел

Много тысяч лет назад люди учились считать предметы. Для этого им пришлось ввести числа и придумывать им название. О том, как появились имена у чисел, ученые узнали, изучая языки разных племен и народов.

Например, у древних людей, живших на Сахалине, числительные зависели от того, какие предметы считают, какую имеют форму.

Прошло много столетий, а может и тысячелетий, прежде чем одни и те же числительные стали применять к предметам любого вида. Ученые считают, что сначала название получили только числа один и два. А все, что шло после двух, называлось «много». С развитием земледелия, скотоводства, охоты, понадобилось называть и другие числа, большие «много». Появилась необходимость называть не только единицы, а десятки и сотни. В русском языке число, следующее за числом десять, получило название «один - на - десять», затем шло число «два - на - десять». Постепенно эти названия чисел были сокращены, человек стал говорить одиннадцать, двенадцать. А когда дошли до числа девятнадцать, пришлось задуматься, как назвать следующее число.

На помощь призвали умножение. Следующее число за девятнадцатью назвали двадцать, т.е. два десятка. Так появилось и число тридцать. Число сорок долгое время называли «четыредцать».

Только 700 лет назад появилось название «сорок». В названиях чисел, следующих за числом сорок, слово «дцать» исчезать. Появляются по- новому устроенные слова: «пятьдесят», «шестьдесят» и так до слова «восемьдесят». Следовало бы ожидать, что девять десятков получат имя «девятьдесят». Такое название нашим предкам было неудобным. Вместо него был введен термин «десяносто», т.е. «десять до ста». В дальнейшем звук «с» был заменен на «в», и число получило наименование «девяносто».

Подобное произошло и с названием сотен. Мы говорим: «сто», «двести», «триста», «четыреста», а потом идут иные названия: «пятьсот», «шестьсот» и т.д.

Такая система счисления называется десятичной и применяется почти у всех народов.

2. Числа-великаны

Самым большим числом, которым пользовались наши предки, жители Древней Руси, было100 миллионов. У наших предков были свои названия больших чисел: 1000-тысяща, 10 000- тьма, 100 000- легион,

1000 000-леорд, 10 000 000- ворон, 100 000 000-колода= 10 воронов.

Числа-гиганты имеют ещё и другие названия: числа-великаны, числа-исполины, астрономические числа .

Для сокращения записи больших чисел давно используется система величин, в которой каждая из последующих в тысячу раз больше предыдущей. (см. Приложение 1)

В этом случае запись числа мало наглядна. Из уроков математики нам известно, что 10³ =1000, 10⁶ = 1000 000, из этого следует, что большие числа можно записать в виде степени числа 10, показатель которой равен числу нулей в записи числа.

Таким образом,

Тысяча - 1000 = 10³

Миллион - 1000 000 - 10⁶

Биллион - 1 000 000 000=10⁹

Триллион - 1000 000 000 000 = 10¹²

Квадриллион - 1000 000 000 000 000=10¹⁵

Квинтиллион - 1000 000 000 000 000 000 = 10¹⁸

Секстиллион - 1000 000 000 000 000 000 000=10²¹

Септиллион - 1000 000 000 000 000 000 000 000=10²⁴

Октиллион - 1000 000 000 000 000 000 000 000 000=10²⁷.

Приложение 2. Таблица чисел-великанов

Надо заметить, что обычные цифровые обозначения весьма больших чисел и их названия употребляются лишь в популярно-научных книгах; в книгах же строго-научных по физике и астрономии пользуются обыкновенно иным способом обозначения. При таком способе обозначения сберегается место и, кроме того, гораздо легче производить над числами различные действия (по пра­вилам, изучаемым в математике)

3. Числовые великаны вокруг и внутри нас

Часто можно встретиться с числовыми великанами. Они присут­ствуют всюду вокруг и даже внутри нас самих - надо лишь уметь рассмотреть их. Небо над головой, песок под ногами, воздух вокруг нас, кровь в нашем теле - все скрывает в себе невидимых великанов из мира чисел.

Числовые исполины небесных пространств для боль­шинства людей не являются неожиданными. Понятно, что если зайдет речь о числе звезд вселенной, об их расстояниях от нас и между собою, об их разме­рах, весе, возрасте - во всех случаях мы неизменно встречаемся с числами, подавляющими воображение своей огромностью. Недаром выражение «астрономиче­ское число» сделалось крылатым. Многие, однако, не знают, что даже и те небесные тела, которые астрономы часто называют «маленькими», оказываются настоящими великанами, если применить к ним привычную земную мерку. Существуют в нашей солнечной системе планеты, которые, ввиду их незначительных размеров, получили у астрономов наименование «малых».

Песок под нашими ногами также вводит нас в мир числовых исполинов. Недаром сложилось издавна выра­жение: «бесчисленны, как песок морской». Древ­ние недооценивали многочисленность песка, считая ее одинаковой с многочисленностью звезд. В старину не было телескопов, а простым глазом мы видим на небе всего около 3500 звезд (в одном полушарии). Песок на морском берегу в миллионы раз многочисленнее, чем звезды, доступные невооруженному зрению.

Величайший числовой гигант скры­вается в том воздухе, которым мы ды­шим. Каждый кубический сантиметр воздуха, каждый наперсток заключает в себе 27 квинтиллионов (т. е. 27 с 18 нулями) мельчайших частиц, называе­мых «молекулами». Невозможно даже представить себе, как велико это число. Если бы на свете было столько людей, для них буквально недостало бы места на на­шей планете. В самом деле: поверх­ность земного шара, считая все его материки и океаны,- равна 500 мил­лионам кв. км. Переведем в квадратные метры, получим 500 000 000 000 000 кв. м. Поделим 27 квинтиллионов на это число, и мы полу­чим 54 000. Это означает, что на каждый квадратный метр земной поверхности приходилось бы более 50 тысяч человек!

Числовые великаны скрываются и внутри человеческого тела. Покажем это на примере нашей крови. Если каплю ее рассмотреть под микроскопом, то окажется, что в ней плавает огромное множество чрезвычайно мелких телец красного цвета, ко­торые и придают крови ее окраску. Каждое такое «красное кровяное тельце» имеет форму крошечной круглой по­душечки, посредине вдавленной. Все они у че­ловека примерно одинаковых размеров и имеют в попе­речнике около 0,007 мм, а толщину - 0,002 мм. Зато число их огромно. В крошечной капельке крови, объемом 1 куб. мм, их заключается 5 миллионов. Сколько же их всего в нашем теле? В теле человека примерно в 14 раз меньше литров крови, чем килограммов в его весе. Если вы весите 40 кг, то крови в вашем теле около 3 литров, или 3 000 000 куб. мм. Так как каждый куб. мм заключает 5 миллионов красных телец, то общее число их в вашей крови: 5000 000x3000 000=15 000 000 000 000.

15 триллионов кровяных телец! Какую длину займет эта армия кружочков, если выложить ее в ряд один к другому? Нетрудно рассчитать, что длина такого ряда была бы 105 000 км. Более чем на сто тысяч километров растя­нулась бы нить из красных телец вашей крови. Ею можно было бы обмотать земной шар по экватору: 105 000 : 40 000=2,5 раза, а нитью из кровяных шариков взрослого человека - три раза.

Объясним, какое значение для нашего организма имеет такое измельчение кровяных телец. Назначение этих телец - разносить кислород по всему телу. Они захваты­вают кислород, когда кровь проходит через легкие, и вновь выделяют его, когда кровяной поток заносит их в ткани нашего тела, в его самые удаленные от легких уголки. Сильное измельчение этих телец способствует выполнению ими этого назначения, потому что чем они мельче, при огромной численности, тем больше их по­верхность, а кровяное тельце может поглощать и выде­лять кислород только со своей поверхности. Расчет пока­зывает, что общая поверхность их во много раз превос­ходит поверхность человеческого тела и равна 1200 кв. м. Такую площадь имеет большой огород в 40 м длины и 30 м ширины. Теперь вы понимаете, до какой степени важно для жизни организма то, что кровяные тельца сильно раздроблены и так многочисленны: они могут за­хватывать и выделять кислород на поверхности, которая в тысячу раз больше поверхности нашего тела.

Сколько пищи поглощает человек за свою жизнь

Ч

исловым великаном следует на­звать и тот внушительный итог, который получился бы, если бы вы подсчитали, сколько всякого рода пищи поглощает человек за 70 лет средней жизни. Целый желез­нодорожный поезд понадобился бы для перевозки тех тонн воды, хлеба, мяса, дичи, рыбы, картофеля и других овощей, тысяч яиц, тысяч литров молока и т. д., которые человек успевает поглотить в течение своей жизни.

Быстрое размножение

Спелая маковая головка полна крошечных зернышек; из каждого может вырасти целое растение. Сколько же получится маков, если зернышки до единого прорастут? Чтобы узнать это, надо сосчитать зернышки в целой головке. Скучное занятие, но результат так интересен, что стоит запастись терпением и довести счет до конца. Оказывается, одна головка мака содержит (круглым числом) 3000 зернышек.

Что отсюда следует? То, что будь вокруг нашего макового растения достаточная площадь подходящей земли, каждое упавшее зернышко дало бы росток, и будущим летом на этом месте выросло бы уже 3000 маков. Целое маковое поле от одной головки!

Посмотрим, что будет дальше. Каждое из 3000растений принесет не менее одной головки (чаще же несколько), содержащей 3000 зерен. Проросши, семена каждой головки дадут 3000 новых растений, и, следовательно, на второй год у нас будет уже не менее 3000 х 3000 = 9 000 000 растений.

Легко рассчитать, что на третий год число потомков нашего единственного мака будет уже достигать 9 000 000 х 3000 = 27000 000 000.

На пятом году макам станет тесно на земном шаре, потому что число растений сделается равным

81 000 000 000 000 х 3000 = 243 000 000 000 000 000.

Поверхность же всей суши, то есть всех материков и островов земного шара, составляет только 135 миллионов кв. км - 135 000 000 000 000 кв. м. - примерно в 200 раз менее, чем выросло бы экземпляров мака.

Видим, что, если бы все зернышки мака проростами, потомство одного растения могло бы уже в пять лет покрыть сплошь всю сушу земного шара густой зарослью по 2000 растений на каждом квадратном метре. Вот такой числовой великан скрывается в крошечном маковом зернышке!

Сделав подобный же расчет не для мака, а для какого-нибудь другого растения, приносящего меньше семян, мы пришли бы к такому же результату, но только потомство его покрыло бы всю Землю не в пять лет, а в немного больший срок.

Почему же в действительности не наблюдаем мы такого чудовищно быстрого размножения? Потому что огромное большинство семян погибает, не давая ростков: они или не попадают на подходящую почву и вовсе не прорастают, или, начав прорастать, заглушаются другими растениями, или же, наконец, просто истребляются животными. Если бы этого массового уничтожения семян и ростков не было, каждое растение в короткое время покрыло бы сплошь всю нашу планету.

Это верно не только для растений, но и для животных. Не будь смерти, потомство одной пары любого животного рано или поздно заполнило бы всю Землю. Полчища саранчи, сплошь покрывающие огромные пространства, могут дать некоторое представление о том, что было бы, если бы смерть не препятствовала размножению живых существ. В каких-нибудь два-три десятка лет материки покрылись бы непроходимыми лесами и степями, где кишели бы миллионы животных, борющихся между собой за место. Океан наполнился бы рыбой до того густо, что сходство стало бы невозможно. А воздух сделался бы едва прозрачным от множества птиц и насекомых.

Числа великаны в переписи населения

В настоящее время население Земли составляет более 7 миллиардов человек .

Прогноз на 2050 год - 9 миллиардов человек,

на 2100 год - 10 миллиардов человек.

Население Российской Федерации - России

на 1 января 2015 года по оценке Росстата было 146 270 033 постоянных

жителей.

- Резервный фонд России

Объем Резервного фонда на 1 января составляет 4,9 трлн рублей. Правительство имеет право в 2015 году израсходовать 500 млрд рублей из этой суммы. Эти деньги идут на преодоление последствий финансово-экономического кризиса в России.

В повседневной практике, даже при сложнейших вычислениях, редко используются числа больше миллиарда. Астрономы, физики и химики, имеющие дело с большими числами, предпочитают записывать числа с помощью степени числа десять.

Мы с трудом ориентируемся в больших числах, даже миллион как следует, себе не представляем.

Как представить себе 1 000 000 учащихся?

Чтобы это представить, посчитаем, на сколько километров протянулась бы шеренга в 1 000 000 учащихся, если бы каждые 2 из них заняли 1м. Почти от Москвы до Санкт-Петербурга протянулась бы эта шеренга.

Каких размеров достигнет обыкновенный комар, увеличенный в миллион раз?

Длина комара приблизительно равна 5 мм.

5 мм x1 000 000 = 5 000 000мм = 5 км.

Рост человека, увеличенный в миллион раз, достигает 1700км.

Миллион можно назвать карликом по сравнению с таким числом, как миллиард.

Если мы начнем считать подряд до миллиарда в 12 - летнем возрасте, то закончим счет глубоким стариком 100 - летнего возраста, работая ежедневно по 6 часов в сутки.

Миллиард - это не просто великан, а великанище. Ведь совсем небольшой промежуток времени - 1 минута. А миллиард таких минут - эта более 19 столетий. Секунда времени в сравнении с часом нам кажется мгновением. Но миллиард секунд - это около 32 лет.

4. Решение задач

1) Сколько времени потребуется человеку, чтобы сосчитать миллиард зерен, если он в минуту будет считать по 100 зерен.

Решение: По нашему условию, сосчитать до миллиарда человеку потребуется 1 000 000000:100=10 000 000 мин. Или (10 000 000:60=166 667), т. е. Примерно 170 000 ч.или (170000:24=7000) около 7000 суток, т. е. Более 16 лет беспрерывного счета.

2) От земли до Марса около 60млн.км. Сколько времени придется лететь на ракете от земли до Марса, если скорость ракеты будет 10км/ч? Сколько времени потребовалось бы самолету, летящему со скоростью 1000км/ч, чтобы преодолеть это расстояние?

Решение: Ракета будет лететь 60:10=6млн.с, или около 1667ч, что составляет примерно 70 суток. Так как скорость самолета 1000км/ч, то на все расстояние ему потребуется 60 000 ч, или 2500 суток, т.е. примерно 7 лет.

3).В нашей стране проживают около 250 млн. человек. Если все люди встанут в одну шеренгу, то какой длины будет эта шеренга? (Пусть каждый человек занимает место длиной в 50см).

Решение: 250 000 000·50 =12 500 000 000см, т.е. 125 000 км

4) Самая высокая гора на Земле - Джомолунгма. Её высота 8848м. Сколько этажей имел бы дом высотой с эту гору, если считать, что расстояние между этажами 4м.

Решение: 8848:4=2212 этажей

5. Применение чисел - великанов в жизни

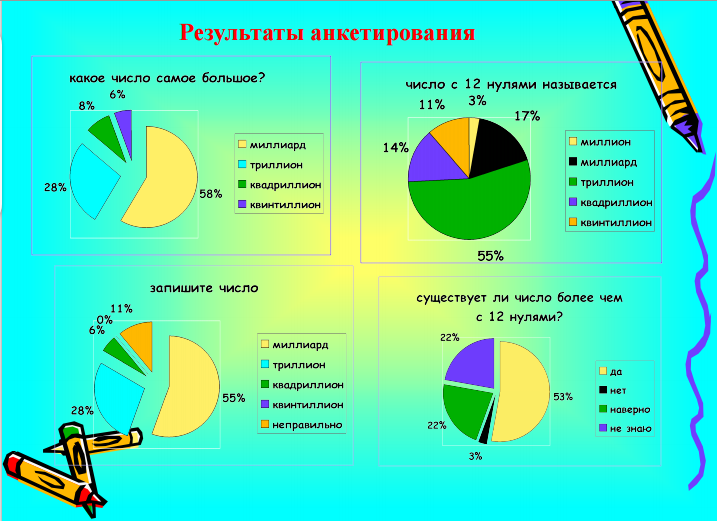
1) При исследовании проблемы в МКОУ Новоярковской СОШ было проведено анкетирование. В анкете представлены следующие вопросы:

- Какое число самое большое?

- Запишите число миллион, миллиард, триллион, квадриллион, и др.?

- Как называется число с 12 нулями?

- Существуют ли числа более чем с 12 нулями?

- Что больше биллион или миллиард?

Результаты следующие:

Из 35 опрошенных 11 учащихся самым большим числом назвали триллион, 19 учащихся - миллиард, а 3 ученика- квадриллион, 2 ученика - другие классы.

31 из опрошенных правильно записали числа миллион, миллиард, у пятерых не хватает нулей, 3 учащихся правильно записали триллион, 1 квадриллион.

На вопрос «Как называется число с 12 нулями?» 19 учеников назвали правильный ответ. У других нет ответа.

На последний вопрос из опрошенных 21 учеников ответили - «да», 10 - «наверно», 3 учеников ответили «не знаю», 1 - нет.

Вывод: не все учащиеся знают числа, предложенные в анкете (Приложение 3).

Заключение

Проделанная исследовательская работа помогла узнать, как зародилась наука о числах, как она развивалось, какие трудности встречались на ее пути и какие ученые занимались изучением чисел и их свойств. Узнав историю возникновения чисел, систем счисления, название классов, расширила свой кругозор в области математики, а именно по вопросу числа- великаны. Была удивлена, что числа великаны и названия их появились давно. Оказывается, они окружают нас повсюду.

Подробно изучив классы, могу называть и записывать числа- великаны, использовать знания при решении задач. Через практическую деятельность - вычисления, сравнения попыталась представить, насколько эти числа огромны. Полученные знания помогут в дальнейшем в изучении предметов физика, химия, астрономия. Планирую продолжить изучение чисел их свойств. Зная, что существуют числа- великаны, хочется иметь представление о числах- карликах.

Гипотеза «Если узнаем историю возникновения чисел, системы счисления и название классов, тогда легко будем читать и писать большие числа. Сможем избежать трудностей при чтении, сталкиваясь на практике с числами-великанами нашла свое утверждение.

Приложение 1

1-й класс- 1000 единиц - просто тысяча

2-й класс- 1000 тысяч - 1 миллион

3-й класс -1000 миллионов - 1миллиард или биллион

4-й класс -1000 биллионов - 1 триллион

5-й класс -1000 триллионов - 1 квадриллион

6-й класс -1000 квадриллионов- 1 квинтиллион

7-й класс- 1000 квинтиллионов - 1секстиллион

8-й класс -1000 секстиллионов - 1 септиллион

9-й класс -1000 септиллионов - 1октиллион

10-й класс -1000 октиллионов - 1 нониллион

11-й класс -1000 нониллионов - 1 дециллион

12й класс- 1000 дециллионов - ундециллион.

Приложение 2

Таблица чисел - великанов

Длинная

шкала

тысяча

10³

10³

миллион

10⁶

10⁶

миллиард

(10⁹)

10⁹

биллион

10⁹

10¹²

биллиард

-

10¹⁵

триллион

10¹²

10¹⁸

триллиард

-

10²¹

квадриллион

10¹⁵

10²⁴

квадриллиард

-

10²⁷

квинтиллион

10¹⁸

10³⁰

квинтиллиард

-

10³³

секстиллион

10²¹

10³⁶

секстиллиард

-

10³⁹

септиллион

10²⁴

10⁴²

септиллиард

-

10⁴⁵

октиллион

10²⁷

10⁴⁸

октиллиард

-

10⁵¹

нониллион

10³⁰

10⁵⁴

нониллиард

-

10⁵⁷

дециллион

10³³

10⁶⁰

дециллиард

-

10⁶³

Длинная

шкала

анцентиллион

10³⁰⁶

10⁶⁰⁶

дуоцентиллион

10³⁰⁹

10⁶¹²

трецентиллион

10³¹²

10⁶¹⁸

кватторцентиллион

10³¹⁵

10⁶²⁴

децицентиллион

10³³³

10⁶⁶⁰

ундецицентиллион

10³³⁶

10⁶⁶⁶

сексагинтиллиард

-

10³⁶³

вигинтицентиллион

10³⁶³

10⁷²⁰

третригинтацентиллион

10⁴⁰²

10⁷⁹⁸

септуагинтиллиард

-

10⁴²³

октогинтиллиард

-

10⁴⁸³

нонагинтиллиард

-

10⁵⁴³

центиллиард

-

10⁶⁰³

дуцентиллион

10⁶⁰³

10¹²⁰⁰

анцентиллиард

-

10⁶⁰⁹

дуоцентиллиард

-

10⁶¹⁵

трецентиллиард

-

10⁶²¹

кватторцентиллиард

-

10⁶²⁷

децицентиллиард

-

10⁶⁶³

ундецицентиллиард

-

10⁶⁶⁹

трицентиллион

10⁹⁰³

10¹⁸⁰⁰

квадрингентиллион

10¹²⁰³

10²⁴⁰⁰

квингентиллион

10¹⁵⁰³

10³⁰⁰⁰

сесцентиллион

10¹⁸⁰³

10³⁶⁰⁰

септингентиллион

10²¹⁰³

10⁴²⁰⁰

окстингентиллион

10²⁴⁰³

10⁴⁸⁰⁰

нонгентиллион

10²⁷⁰³

10⁵⁴⁰⁰

миллиллион (или милиаиллион)

10³⁰⁰³

10⁶⁰⁰⁰

дуомилиаллион

10⁶⁰⁰³

10¹²⁰⁰⁰

тремиллиаллион

10⁹⁰⁰³

10¹⁸⁰⁰⁰

квинквемилиаллион

10¹⁵⁰⁰³

10³⁰⁰⁰⁰

дуцентдуомилианонгентновемдециллион

10³⁰⁸⁷⁶⁰

10⁶¹⁷⁵¹⁴

милиамилиаиллион

10^3000003

10^6000000

дуомилиамилиаиллион

10^6000003

10^12000000

гуголплекс[1]

10¹⁰¹⁰⁰

10¹⁰¹⁰⁰

зиллион</</u>

10^3×n+3

10^6×n

Приложение 3

Анкета

1. Какое число самое большое?

2. Число с 12 нулями называется: миллион, миллиард,триллион,квадриллион,квинтиллион?

3. Запишите число миллиард, триллион, квадриллион, квинтиллион.

4. Существует ли число более, чем с 12 нулями?

15