Урок математики Понятие десятичной дроби

Ольга Геннадьевна Бурлакова, учитель математики

МБОУ СОШ № 4, г. Ленск РС(Я)

Разработка урока математики

Урок может проводится в 5 или 6 классе в зависимости от программы.

Тема урока. Десятичная дробь

Цель урока:

- ввести понятие десятичной дроби, выработать навыки чтения и записи десятичных дробей;

- ознакомление учащихся с историческим материалом;

- активизировать работу учащихся за счет вовлечения их в игру, привитие интереса к предмету;

План урока.

1. Организационный момент.

2. Подготовительный этап (историческая справка).

3. Мотивационный этап.

4. Ориентировочный этап.

5. Непосредственное закрепление (Математический диктант с самопроверкой).

6. Домашнее задание.

7. Итог урока.

Оборудование: таблица с разрядами, карточки с домашним заданием, карточки с заданиями для закрепления.

ХОД УРОКА.

1. Организационный этап.

Приветствие детей, задачи урока.

2. Подготовительный этап.

В истории было много разных способов для обозначения натуральных чисел, но в конце концов «победила» одна - десятичная позиционная система записи, которой в настоящее время пользуется весь мир.

Например, 23059789

Учащимся предлагается назвать все разряды.

Похожая история произошла и с обозначением дробей. Дроби, как известно, возникли в связи с делением предметов на несколько частей. И поскольку в различных практических задачах приходится делить на разное число разных частей - на 5, на 8, на 45 и т.д., то и дроби рассматриваются с самыми различными знаменателями - и т.д. При этом вычисления с дробями гораздо сложнее, чем вычисления с натуральными числами, в чем каждый уже убедился на собственном опыте. А в Древнем Египте такие вычисления могли проводить только жрецы - самые образованные люди общества того времени.

Например,

учащимся предлагается назвать числитель, знаменатель дроби

указать целую и дробную части

Вычислить =

3. Мотивационный этап.

Около пяти столетий назад голландский математик Симон Стевин изобрел способ записи дробей, который позволил резко изменить сложность вычислений. Его идея заключалась в том, чтобы ограничить число рассматриваемых дробей только дробями со знаменателями 10, 100, 1000 и т.д.

Например,

Позднее дроби со стандартным знаменателем вида 1 с нулями стали записывать в строчку.

Например, 0,3; 2,47; 0,156; 5,2309 и стали называть десятичными.

Запятая пришла не сразу.

Например, 35 912

35 9 1 1 2 2 3

35, 912

4. Ориентировочный этап.

Десятичные дроби читают также, как и обыкновенные, но с обязательным указанием целых единиц. (доже, если их «ноль»). При этом целая часть десятичной дроби отделяется от дробной части запятой. Например,

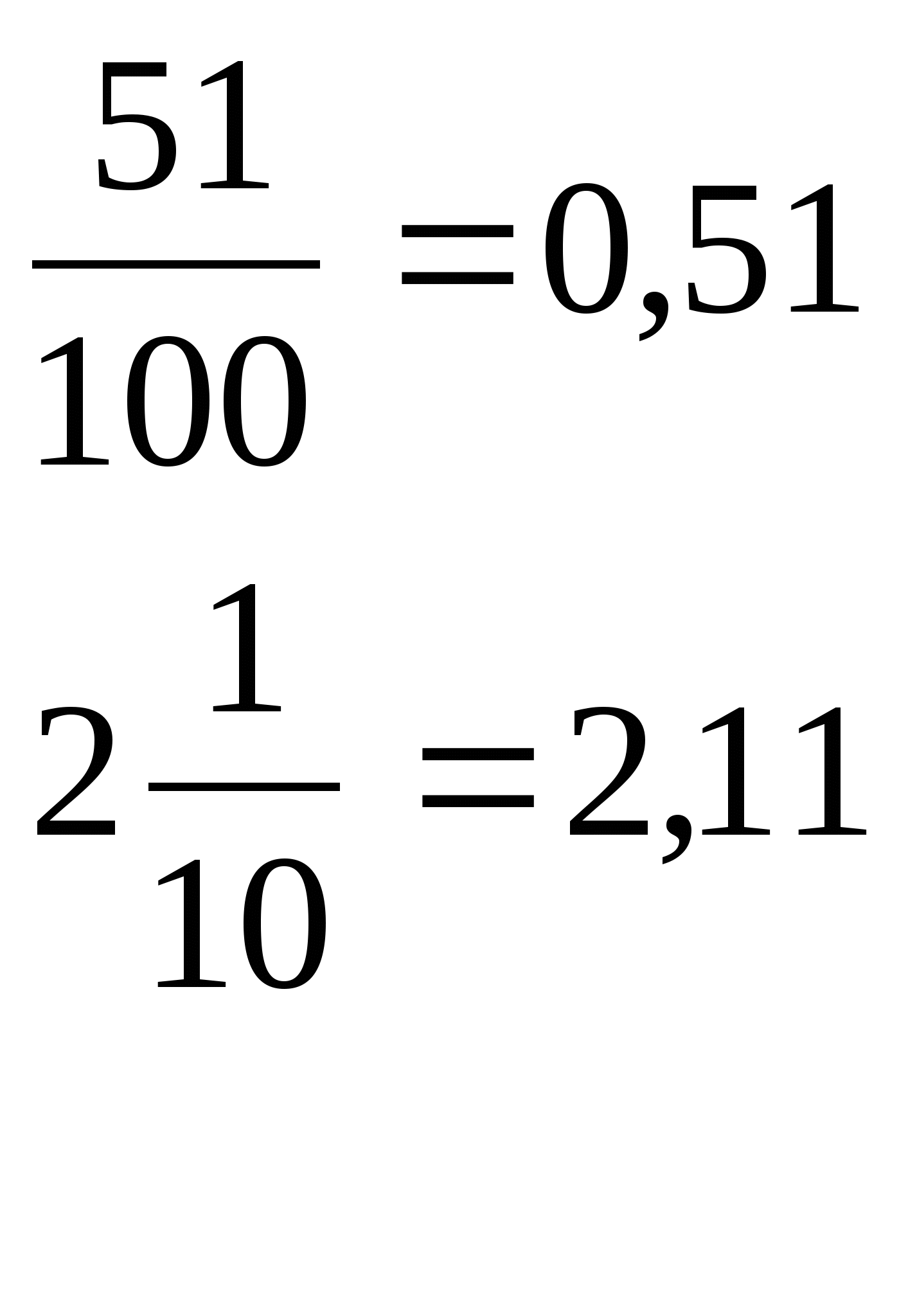
Разряды дробной части

сотни

десятки

единицы

десятые

сотые

тысячные

Десятитысячные

Стотысячные

миллионные

десятимиллионные

стомиллионные

миллиардные

2

5

3

3

6

7

5

1

2

8

1

3

1

0

9

0

9

1

3

2

4

1

Способ записи десятичных дробей является обобщением записи натуральных чисел.

В записи натурального числа значение цифры зависит от того, в каком разряде она находится. Единицы двух соседних разрядов отличаются друг от друга в 10 раз.

Для записи десятичных дробей используют новые разряды, которые пишут справа от разряда единицы, поставив после него запятую.

1. й разряд после запятой - десятые доли ();

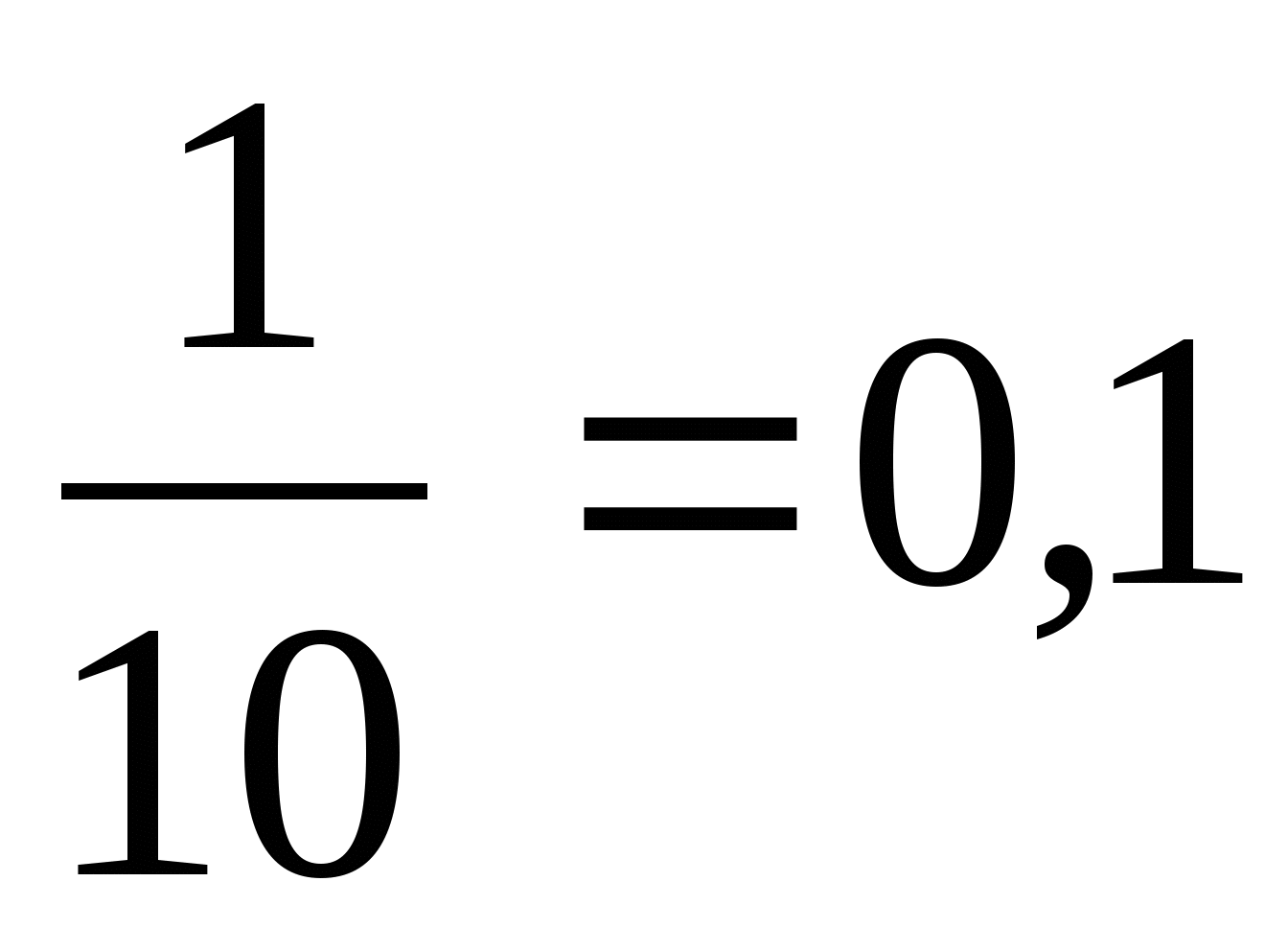2. й - сотые доли ();

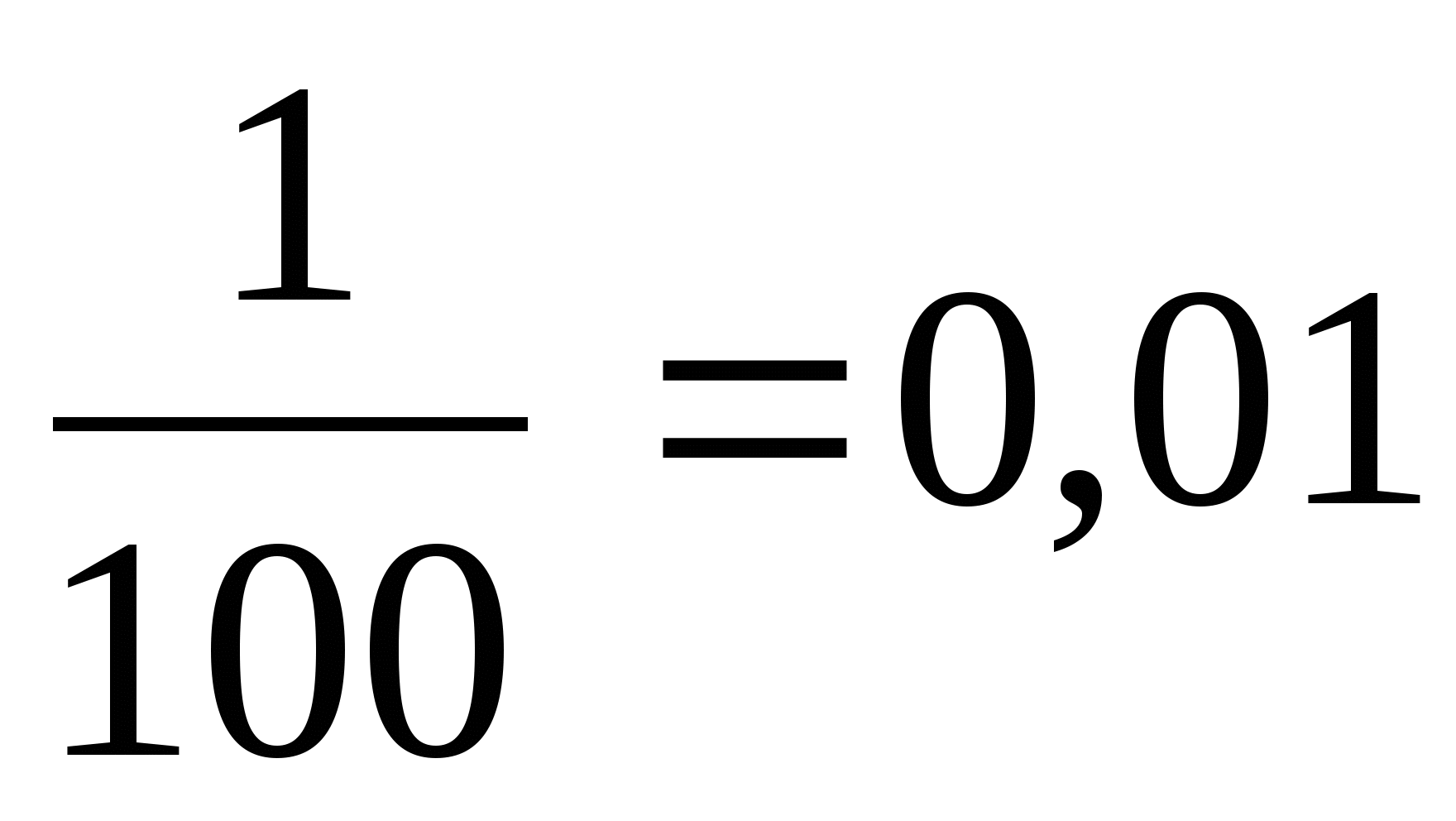3. й - тысячные доли и т.д.

Отсутствие единиц в разряде обозначается нулями.

При чтении десятичной дроби сначала называют её часть, стоящую до запятой с добавлением «целых», а затем часть, стоящую после запятой, с добавлением последнего разряда.

Из приведенных примеров (в начале урока) видно, что в десятичной дроби после запятой стоит столько же цифр, сколько цифр в числителе соответствующей ей обыкновенной дроби.

Например, три цифры и в её десятичной записи три знака после запятой.

В этих примерах есть ещё одна особенность: в числителях дробей столько же цифр, сколько нулей в знаменателе. А как быть в случае, когда это не так?

Например,

Это несложно, если применить маленькую «математическую хитрость»: разрешить приписывать нули к натуральному числу слева, считая что оно не изменится

Например, 72 = 072 = 0072 = ….

2 нуля 2 знака 5 нулей 5 знаков

Таким образом, для дробей, имеющих знаменатель 1 с нулями, можно пользоваться следующим алгоритмом.

1. Уравнять, если необходимо, число цифр в числителе с числом нулей в знаменателе.

2. Записать целую часть.

3. поставить запятую отделяющую целую часть от дробной.

4. Записать числитель дробной части.

Например,

Знаки, стоящие в десятичной дроби после запятой, называются десятичными знаками. По числу десятичных знаков можно узнать чему равен знаменатель дроби.

Например, 7,025 имеет 3 десятичных знака, значит в знаменателе должно быть 3 нуля, т.е. 1000.

Таким образом, десятичная запись числа указывает его целую часть, числитель и знаменатель. Поэтому любую десятичную дробь легко записать в виде обыкновенной дроби (простой или смешанной).

Например,

0, 35 =

Приписывание одного, двух и т.д. нулей к знакам, стоящим после запятой, не изменяет десятичной дроби, т.к. является по сути умножением числителя и знаменателя соответствующей обыкновенной дроби на 10, 100, 1000 и т.д.

Например, 0,7 = 0,70 = 0,700 = …

9,8 = 9,80 = …

Это означает, в частности, что натуральное число также можно представить в виде десятичной дроби, и при этом бесконечным числом способов.

Например, 31 = 31,0 = 31,00 = …

5. Непосредственное закрепление.

1. № 244. [2]Назовите число единиц каждого разряда:

а) 0,27; 34,206; 19,041;

б) 123,5476; 6902,0584.

2. № 245. [2]Дано число 242,341. В каких разрядах записана цифра 2? 3? 4? 1?

3.Дано число 123,456789. Какая цифра записана в разряде:

а) сотен; б) сотых; в) десятков; г) десятых; д) единиц; е) тысячных; ж) стотысячных; з) десятитысячных; и) миллионных.

4. Прочитайте десятичные дроби

0,2; 5,6; 0,04; 25,18; 1,049; 8,007; 0,0005; 12,0321; 0,6042; 3,000096.

5. Игра. Передвигаем запятую.[4]

В числе 1030405 влево.

В числе 0,08704 вправо.

6. Записать в виде десятичной дроби и прочитать:[3]

а)

б)

7. Записать короче десятичную дробь:[3]

а) 4,8000; б) 002,900200; в) 71,00000.

8. № 248. [2]Записать десятичные дроби:

а) ноль целых пять десятых;

б) шестнадцать целых тридцать одна сотая;

в) десять целых восемь сотых;

г) пят целых триста восемь тысячных;

д) ноль целых двадцать пят тысячных;

9. Игра.[1] Среди приведенных ниже дробей найди дроби, равные 2,17. Из соответствующих им букв составь название животного на котором можно отправиться в путешествие по северному полюсу.

К 2, 017 Л 2,170 О 2,1700 И 2,0017 Е 02,17 Т 21,70

Ь 02,170 А 2,0107 С 20,17 Н 002,17.

10. Самостоятельная работа (по одному человеку у доски).

1. Записать в виде десятичных дробей

7 целых 8 десятых

5 целых 45 сотых

0 целых 59 сотых

78 целых 1 сотая

4 целых 601 тысячная

76 целых 32 тысячных

6 целых 6 тысячных

0 целых 2 сотых

9 целых 3 тысячные

78 целых 5 тысячных

33 целых 8 десятых

3 целых 4 тысячных

2. Записать десятичные дроби в виде обыкновенных дробей и результат, если возможно сократить.

0,4; 0,9; 0,72; 0,92; 0,25; 0,375; 0,632.

6. Итог урока

12. Математический диктант.[4]

1. Записать в виде дроби

3 5

3. Записать короче.

5,100 31,090

4. Записать в виде десятичной дроби.

70 целых 32 тысячные 3 целых 4 тысячных

7. Домашнее задание.

1) № 250

2) Карточка. [1]

1. Записать числа в виде десятичной дроби.

2. Выберите дроби, у которых в разряде десятых стоит четная цифра, в разряде сотых нечетная цифра, а в разряде тысячных цифра, которая делится на 3. из букв, соответствующих данным дробям, составьте название реки.

Н 3,940 И 8,235 А 0,413 О 0,876 Р 6,198 Т 9,401 Л 5,2394

Й 4,7139 С 0,2945 Е 0,56666 В 5,23941 Г 1,699508.

Литература.

1. Дорофеев Г.В., Петерсон Л.Г. Математика 5 класс. Часть 2. - М.: Издательство «Ювента», 2002. - 240 с.: ил.

2. Математика. 6 класс: Учебник для общеобразовательных учебных заведений/ Г.В. Дорофеев, С.Б. Суворова, И.Ф Шарыгин и др.; Под ред. Г В. Дорофеева, И.Ф. Шарыгина. - 4-е изд. - М.: Дрофа, 1999.

3. Математика: Учебн. Для 5 класса сред шк./ Н.Я Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И. Жохов. - М.: Просвещение, 1990.

4. Мерзляк А.Г., ПолонскийВ.Б, Рабинович Е.М., Якир М.С.. Сборник задач и контрольных работ по математике для 6 класса. - М.: Илекса, Харьков: Гимназия, 1998.