Урок по математике Основное своЙство дроби

Основное свойство дроби

Представьте себе такую ситуацию.

За столом 3 человека и 5 яблок. Делятся 5 яблок на троих. Каждому достается по яблока.

А за соседним столом еще 3 человека и тоже 5 яблок. Каждому опять по .

При этом всего 10 яблок и 6 человек. Каждому по .

Но это одно и то же.

. Эти дроби эквивалентны.

Можно увеличить в два раза количество людей и в два раза количество яблок. Результат будет тем же самым.

В математике это формулируется так:

Если числитель и знаменатель дроби умножить или разделить на одно и то же число (не равное 0), то новая дробь будет равна исходной.

Это свойство иногда называют «основным свойством дроби».

Примеры эквивалентных дробей

1. Путь от города до деревни - 7 км.

Мы идем по дороге и определяем пройденный путь по километровым столбикам. Пройдя три столбика, три километра, мы понимаем, что прошли пути.

Но если мы не видим столбиков (может, их не установили), можно путь считать по электрическим столбам вдоль дороги. Их 20 штук на каждый километр. То есть всего 140 на всем пути. Три километра - столбов. То есть мы прошли 60 из 140 столбов, .

2. Дробь на координатной плоскости можно отмечать точкой. Чтобы изобразить дробь отметим точку с координатой 3 по оси и 4 по оси . Проведем прямую из начала координат через нашу точку.

На этой же прямой будет лежать и точка, соответствующая дроби .

Они являются эквивалентными: (см. Рис. 1)

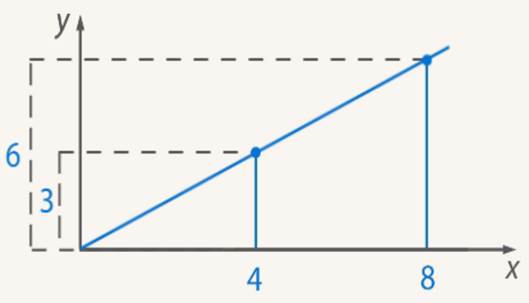
Рис. 1. Иллюстрация к примеру

3. На рисунке 2 два дома. Первый - высотой 6 метров и шириной 4, а второй - высотой 12 метров и шириной 8. Размеры разные, но дома по форме похожи. У них одинаковые пропорции, одинаковое отношение высоты к ширине.

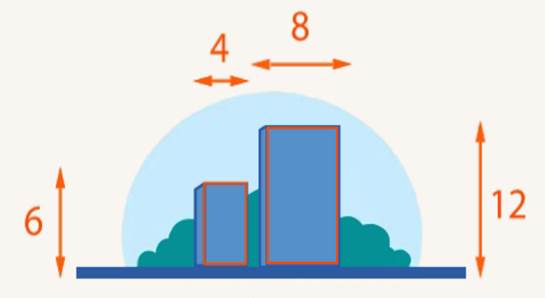
Рис. 2. Иллюстрация к примеру

Сокращение дроби

Дробь можно было получить из умножением числителя и знаменателя на 4:

или из умножением на 2:

Но точно так же можно и вернуться назад.

У дроби можно числитель и знаменатель разделить на 2, получить :

Или числитель и знаменатель разделить на 4, получить :

Вот такой переход от одной дроби к другой с помощью деления числителя и знаменателя на одно и то же число называетсясокращением дроби.

У дроби можно разделить числитель и знаменатель на 100. Получим .

Это эквивалентная запись, но она короче. Мы сократили запись. Сократили дробь:

Сократимые и несократимые дроби

Посмотрим еще раз на цепочку эквивалентных дробей.

Дробь можно сократить на 2 и получить или сократить на 4 и получить .

Дробь нам не получится сократить до или , зато легко сократить на 5 и получить .

Только одну дробь из представленных мы не можем сократить: .

Такая дробь называется несократимой. Ее нельзя сократить.

Остальные сократимые. Их можно сократить.

Пример 1

Рассмотрим дробь .

Чтобы понять, можно ли ее сократить, нужно узнать, существует ли число, на которое делится и числитель, и знаменатель, есть ли общий делитель.

42 делится на 2, но 273 на 2 не делится.

42 делится на 3 (сумма цифр 6 делится на 3), и 273 делится на три (сумма цифр 12).

Значит, мы можем поделить числитель и знаменатель на 3, сократить дробь на 3.

Можно ли сократить полученную дробь дальше?

14 делится на 2 и на 7.

91 не делится на 2, но на 7 делится.

Значит, дробь можно сократить на 7.

Для чисел 2 и 13 нам уже не найти общего делителя.

Дробь несократима.

Не всегда легко, глядя на дробь, понять, можно ее сократить или нет.

Что нам может помочь в этом?

Чтобы сократить дробь, нужно найти общий делитель для числителя и знаменателя.

Но делители числа и его множители - это одно и то же.

2 и 5 - это множители, но на них можно разделить. Поэтому они же и делители.

То есть разложение на множители - это и разложение на делители.

Вернемся к нашему примеру.

Если бы числитель и знаменатель были разложены на множители, мы бы сразу поняли, как сократить дробь.

Общие множители (делители) - 3 и 7. На них и сокращаем.

Пример 2

Сократить дробь, разложив на множители числитель и знаменатель.

Разложим 60 на множители:

Разложим 126 на множители:

Сократим на общие множители, на 2 и на 3. Больше общих множителей (делителей) нет. Перемножим оставшиеся множители:

Задача

В школе 4 первых класса, и в каждом учится 27 учеников.

Есть 12 коробок мандаринов, в каждой по 45 штук. Сколько каждому первокласснику достанется мандаринов, если их поделить поровну?

Понятно, что надо количество мандаринов разделить на количество первоклассников.

Найдем и то и другое.

первоклассников.

мандаринов.

Осталось разделить.

мандаринов на первоклассника.

Но можно было и упростить себе задачу, ведь у нас уже было разложение на множители:

Не будем сразу считать, сколько мандаринов и сколько учеников. Сначала сократим нашу дробь. 12 и 4 делятся на 4. 3 и 27 делятся на 3.

Это решение оказалось проще.

Задание 1

Сейчас самостоятельно сократите следующие дроби:

Проверка:

Задача 2

Докажите, что дробь несократима:

Проверка:

разложим на простые множители числитель и знаменатель:

Общих множителей (общих делителей) нет. Значит, сократить невозможно. Дробь несократима.

Такие числа, как 220 и 273, не имеющие общих делителей, кроме 1, мы называем взаимно простыми.

То есть можно сказать про несократимую дробь следующее: дробь несократима, если ее числитель и знаменатель - взаимно простые числа.

Заключение</</p>

Подведем итог.

1. Сократить дробь - означает разделить ее числитель и знаменатель на одно и то же число (не равное нулю). В результате получаем равную (эквивалентную) дробь, но с меньшими числителем и знаменателем.

2. Чтобы сократить дробь, нужно последовательно проверять, на что делятся числитель и знаменатель. Если находятся общий делитель, то на него и сокращать.

3. Если разложить числитель и знаменатель на множители, то это упростит сокращение.

Всегда ли нужно сокращать?

Фраза: «Цена выросла на 20 %» буквально означает «цена выросла на », так как .

Дробь можно сократить. Получится .

Мы могли бы сказать: «цена выросла на ».

Это, конечно, то же самое. Но общая договоренность - говорить в процентах. Поэтому удобнее оставить эту величину в процентах, не сокращая дробь.

Сокращение - это инструмент. Но мы не обязаны его применять, если не считаем, что так станет проще.