Преобразование выражений, содержащих квадратныекорни

: Тема урока: Преобразование выражений, содержащих квадратные корни

Тип урока: Урок обобщения и систематизации знаний

Цель урока:

• проверить уровень усвоения темы путем дифференцированного опроса учащихся.

Задачи урока:

• формировать у учащихся адекватную самооценку при выборе уровня трудности самостоятельной работы;

• развивать математическую речь при комментировании решения, при составлении алгоритмов выполнения заданий;

• воспитывать навыки самоконтроля и взаимоконтроля;

• развивать самостоятельность и творчество.

Оборудование:Компьютерный класс, экран ,оценочный лист и карточки.

Ход урока

I. Организационный момент Учитель сообщает тему урока, формулирует цель и задачи урока

.

Подвести итоги сегодняшнего урока поможет оценочный лист.

Рабочая карта урока есть у каждого из учащихся. Сюда необходимо вносить баллы, полученные за каждый этап урока. Одну из оценок поставит сосед по парте, а одну - учитель, если учащийся будет работать у доски. Бонусные баллы - за активность. В конце урока будет подведен итог и выставлена отметка за усвоение темы: «Арифметический квадратный корень».

II Устная работа.

Найдите значение: √16, √100, √49, √81, √0,25, √0,09; √400, √121, √3600



√25*36, √25*81, √2500*49, √0,64*25, √0,81*0,04



√4/9, √1/64, √36/49, √81/100, √9/25, √36/121



√2², √3,8², √4,3², √(-1,3)², √(-3,1)²



(√5)², (√8)², (√100)², (√а)², (√в)².





Вынесите множитель за знак корня: √20, √75, √600, √28, √99

Внесите множитель под знак корня: 6√2, 5√6, 3√2



2√а, 1/2√8х, 6√1/6m





Приведите подобные слагаемые: 7√3 + 2√3 - 6√3 = 3√3



6√7 - 5√7 + √7 = 2√7



5√х + 11√х - 6√х = 10√х

Каждый, кто правильно ответил на вопрос, ставит в Рабочую карту урока соответствующее количество баллов:

III На этом этапе урока пишем графический диктант.

Учащиеся отвечают на вопросы:

1. Корень из произведения неотрицательных множителей равен про

изведению корней из этих множителей (да).

2. Это верное равенство:

(нет).

3. Арифметическим квадратным корнем из числа а называется любое число, квадрат которого равен а (нет).

4. Корень из дроби, числитель которой неотрицательное число, а знаменатель - положительное, равен корню из числителя, деленному на корень из знаменателя (да).

5. Выражение имеет смысл только при отрицательном значении а (нет).

6. Это верное равенство: (да).

7. Чтобы извлечь корень из степени с четным показателем, достаточно представить подкоренное выражение в виде квадрата некоторого выражения и воспользоваться тождеством (да).

8. Равенство верно при любом значении х (нет)

. Графический диктант: думать придется много, писать - мало.

- ДА ^ - НЕТ (Эти обозначения можно записать на доске для учащихся, плохо воспринимающих информацию на слух).

Проверка

Критерии оценивания графического диктанта)

«5» - нет ошибок

«4» - 1 - 2 ошибки

«3» - 3 - 4 ошибки

«2» - более 4-х ошибок

IV . Тестирование

Решают задания теста, самостоятельно выбирая уровень, отвечающий их знаниям и умениям

На этом этапе урока необходимо применить выученные определения и правила к решению упражнений в ходе выполнения теста.

Код правильных ответов: 122. Критерии оценивания каждого уровня представлены на карточках и на слайде.

Тест.Вариант 1.

Уровень А

Уровень В

Уровень С

1. Вынесите множитель из-под знака корня:

1.;2.;3.;4.

2. Упростите выражение:

1. -6; 2. -12; 3. 3; 4. 12

3. Сократите дробь:

1. ; 2. ;

3. ; 4.

1. Упростите выражение:

1.;2.;3.;4.

2. Сократите дробь:

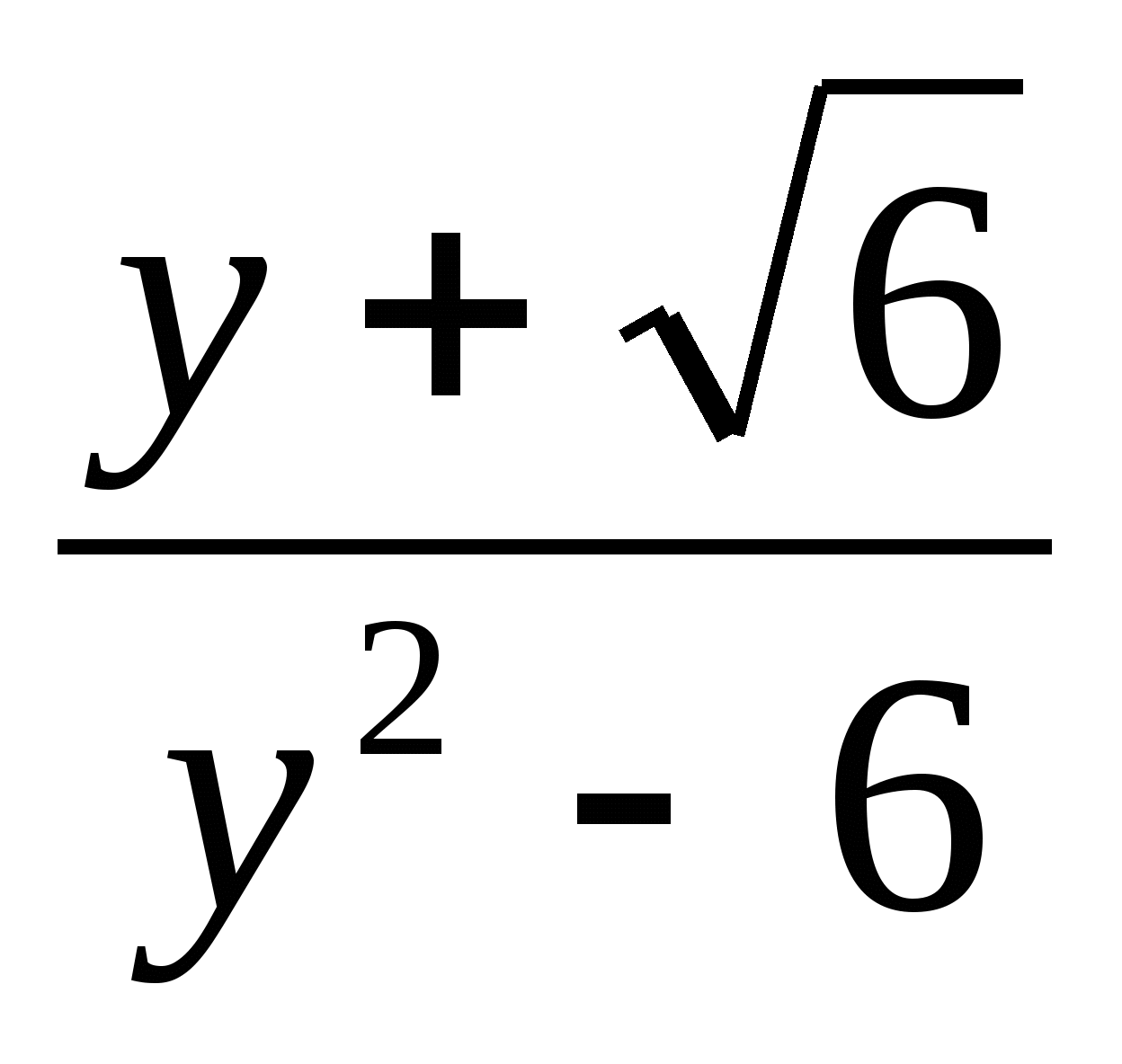
1. ;2. ; 3.; 4.

3. Найдите значение числового выражения:

1. 10; 2. 5; 3. 6; 4. 15

1. Вынесите множитель из-под знака корня:

1. ; 2. ;

3. ; 4.

2. Упростите выражение:

1. ; 2. ;

3. ; 4.

3. Сократите дробь:

1. ; 2. ; 3.; 4.

Критерии оценок:

«3» - все верно или одна ошибка;

«2» - 2 и более ошибок.

Критерии оценок:

«4» - все верно;

«3» - 1 ошибка;

«2» - 2 и более ошибок.

Критерии оценок:

«5» - все верно

«4» - 1 ошибка;

«3» - 2 ошибки;

«2» - все неверно

V Разноуровневая самостоятельная работа

Решают задания, сдают тетради учителю на проверку.



1. Упростите выражения:

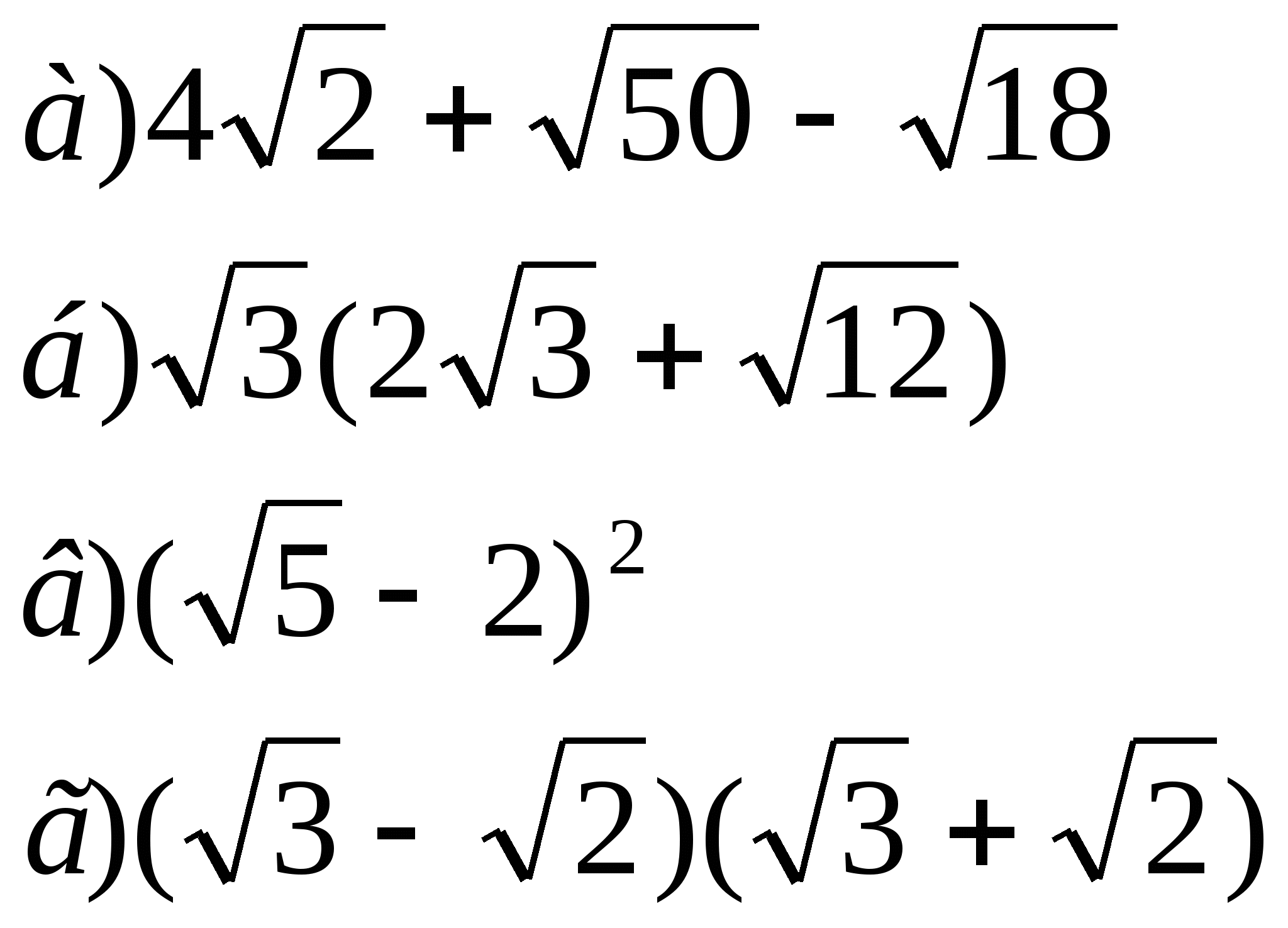
2. Сократите дроби:

3. Решите уравнение, предварительно упростив его правую часть:

1. Упростите выражения:

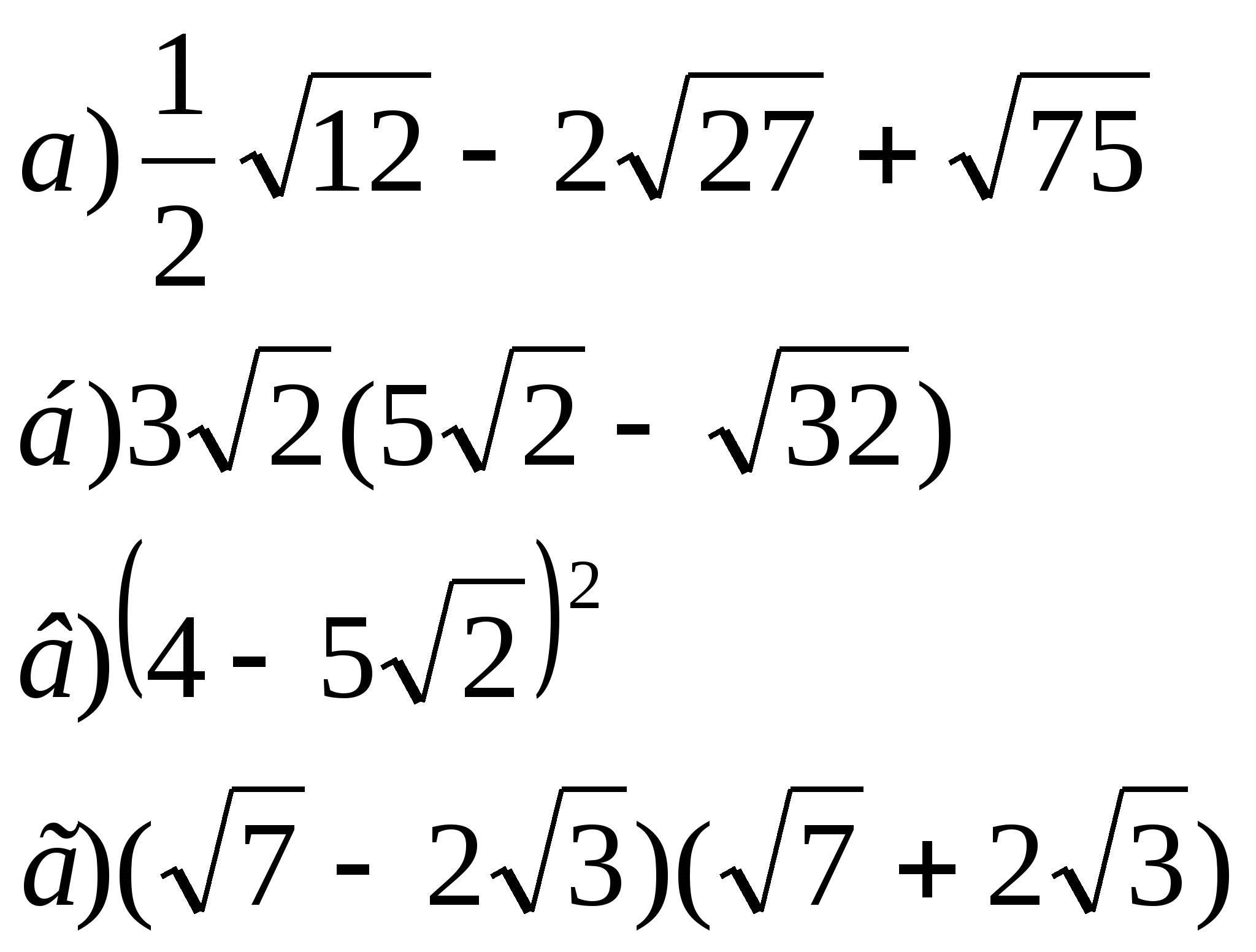
2. Сократите дроби:

3. Докажите, что данное уравнение имеет целые корни, и найдите их:

1. Упростите выражения:

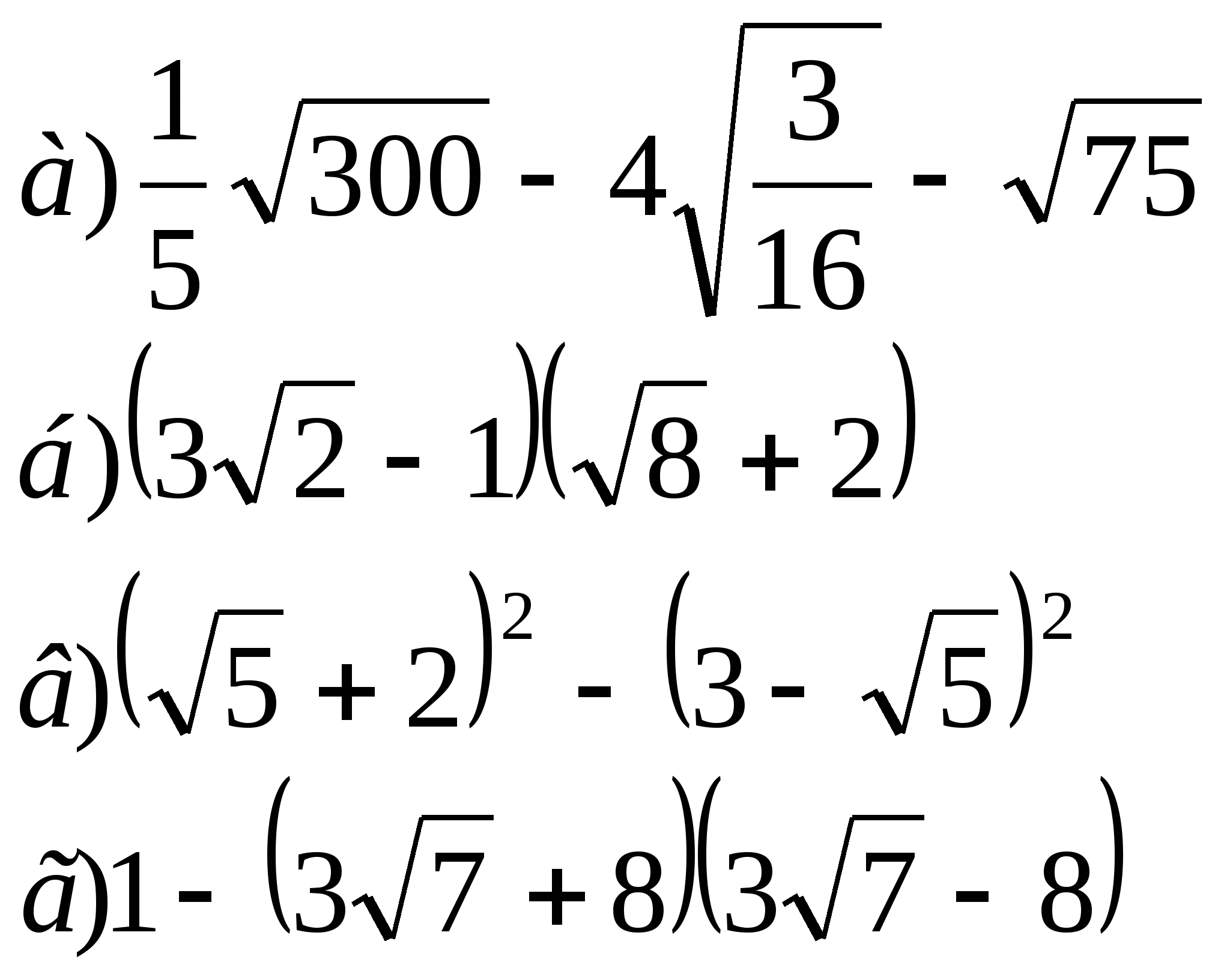
2. Сократите дроби:

3. Решите уравнение:

VI Подведение итогов, рефлексия (3 мин).

Выставляется итоговая отметка в оценочный лист.

Учащиеся подсчитывают общее количество баллов, полученных за урок, выставляют отметку согласно критериям

.

4.





VII . Итог урока (2 мин).

Учитель дает домашнее задание

: Учащиеся получают карточки с домашним заданием

- Сегодня мы повторили определение и свойства арифметического квадратного корня; вынесение множителя за знак корня, внесение множителя под знак корня, формулы сокращённого умножения; ознакомились и закрепили некоторые способы преобразования выражений, содержащих квадратные корни.

Все работали плодотворно, активно и коллективно в течение урока.

Урок окончен.