Конспект урока по алгебре тема: Формулы сокращенного умножения (7 класс)

Алгебра 7 класс

Тема: Формулы сокращенного умножения

Цель: Формирование понятий сокращенного умножения, нахождение наиболее рационального способа умножения многочленов, навыков развития математической речи, формулировок формул.

Форма: урок-поиск

Ход урока

1. Организационный момент.

2. Психологический настрой.

3. Устные упражнения (мотивация обучения)

   1. Найти квадрат выражений

С; -4; 3m; 5х²у³

2. Найти произведение 3х и 6у. Чему равно удвоенное произведение этих выражений?

3. Прочитайте выражения:

(a + b); (a + b)²; (x - y)²; a² + b²; x - y; x² + y²;

4. Выполните умножение:

(х + 6)(х - 5)

5. Объясните как умножить многочлен на многочлен?

(Самостоятельная работа)

4. Новая тема (обучающего характера)

Сегодня мы проводим изучение темы «Умножение многочлена на многочлен». Еще в глубокой древности было подмечено, что некоторые многочлены можно умножать короче, быстрее, чем все остальное. Так появились формулы сокращенного умножения. Их несколько. Сегодня нам предстоит сыграть роль исследователей и открыть две из этих формул.

(Класс делится на 4 группы получают по 2 выражения): каждая группа имеет номер примера, ей предлагается заполнить строку таблицы, перемножив пары двучленов.

Номер задания соответствует номеру группы (пары)

После этого как ребята справились с заданием, один из группы выходит к доске и в правом столбце таблицы записывает полученный ответ.

Средняя часть таблицы закрыта, когда учащиеся заполнили таблицу.

Вопрос: Есть ли место общее в условиях и в ответах упражнения. Можно ли выражения в левом столбце записать короче?

Учитель. Мы практически приступили к исследованию темы урока. Рассмотрим пример: произведение двух выражений, т.е. возводили в квадрат сумму двух выражений.

Пример

Квадрат суммы

Ответ

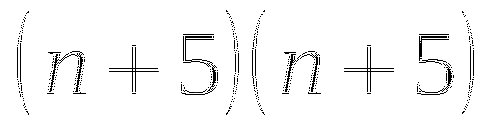
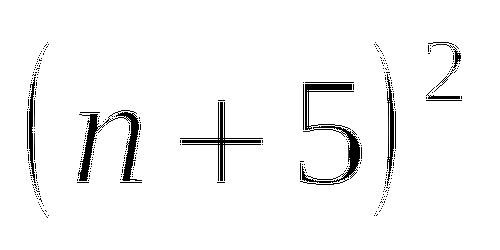
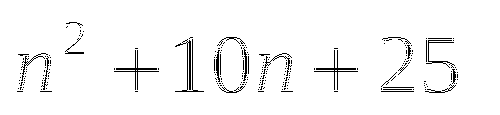
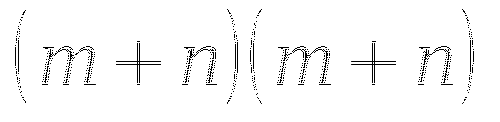
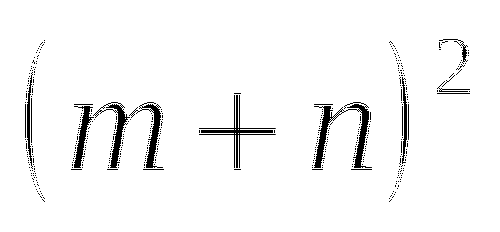
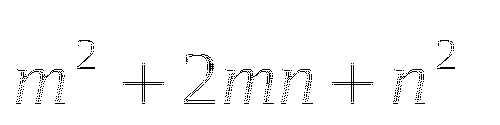
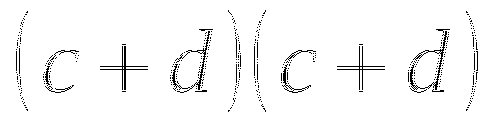
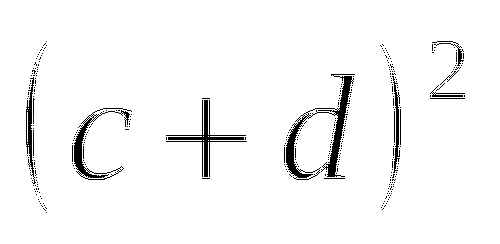
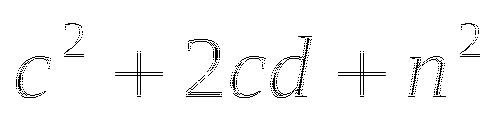
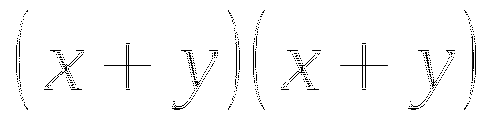
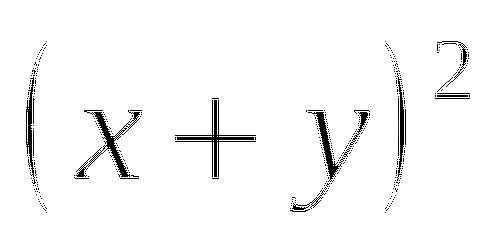
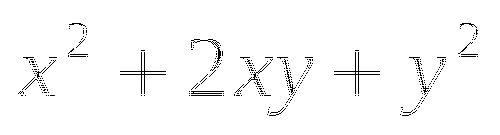
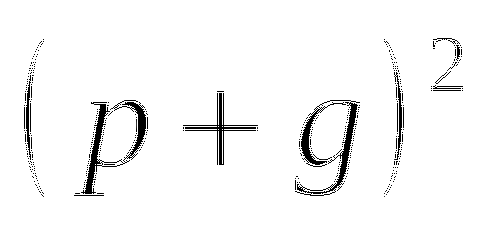
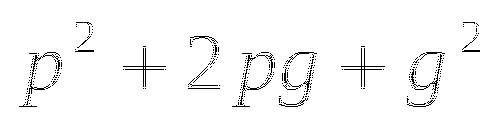
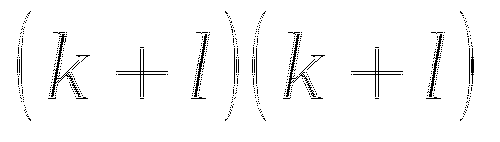
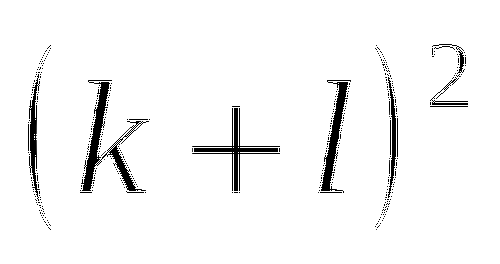
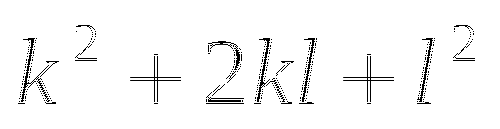
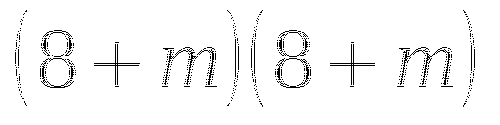
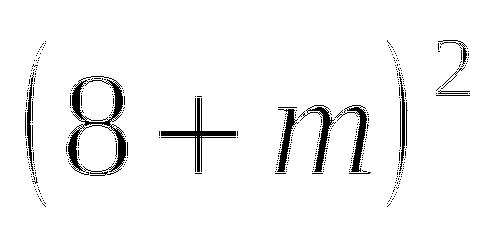
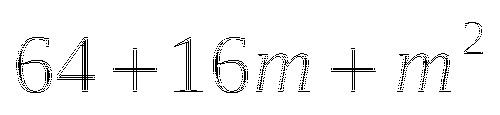
Переходим к обсуждению результатов

- в результате образуется трехчлен, у которого первый член квадрат первого слагаемого, второй - удвоенное произведение первого на второе слагаемое, третий - квадрат второго слагаемого.

(проговаривает каждая группа: квадрат первого слагаемого + удвоенное произведение первого слагаемого на второе + квадрат второго слагаемого, запись формулы)

Вывод:

Учитель. А теперь вопрос: Изменится ли результат, если мы будем возводить в квадрат не , а ? Как изменится это выражение?

В таблице заменить знак «+» на «-» и решают эти же выражения, но со знаком «-»

Вывод: запись формулы

5. Закрепление. 2 человека - запись примеров с полным комментированием.

Проговаривание правила. Обратить внимание на правила - стр.66

6. Работа по таблице.

Пример

Ответы

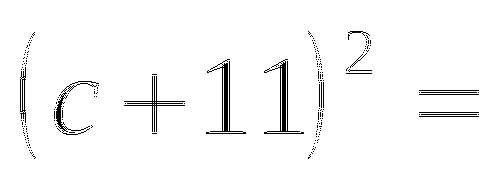
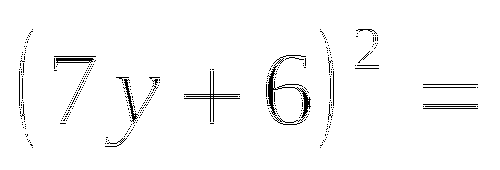
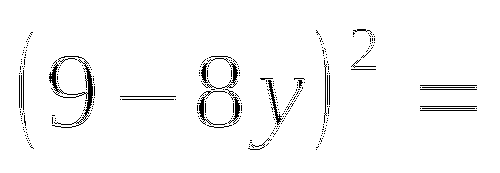
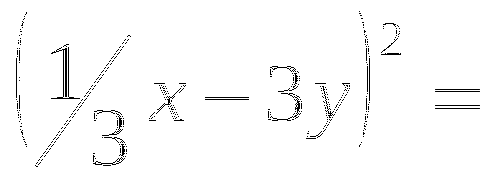
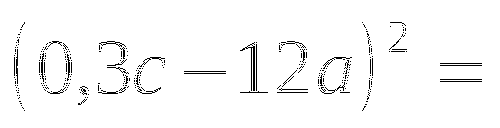
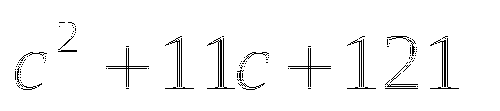
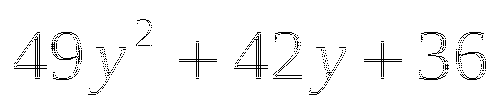
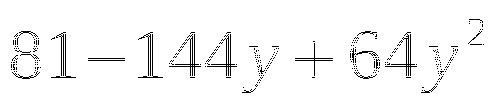
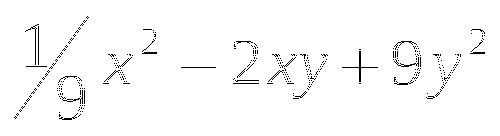
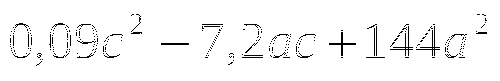
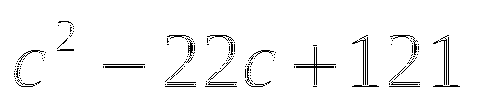
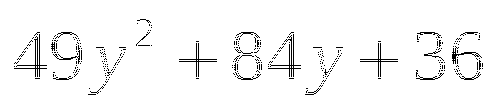
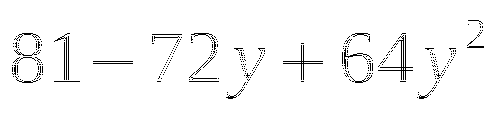
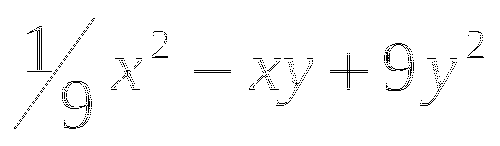
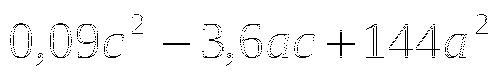
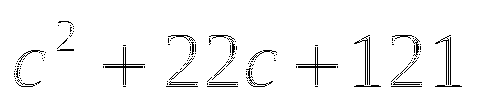
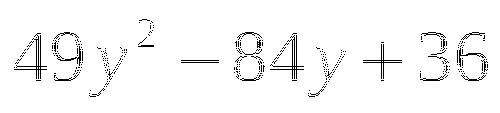
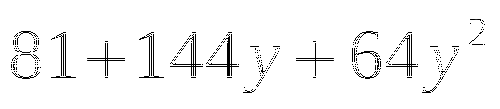
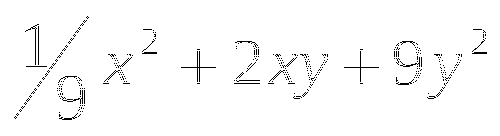
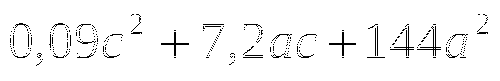
(в таблице 2 ответа не верны, необходимо найти верный ответ и подчеркнуть)

7. Геометрический смысл этой формулы по чертежу стр. 67 рис. 20

Дополнительное сообщение: для устного счета применить эти формулы для чисел:

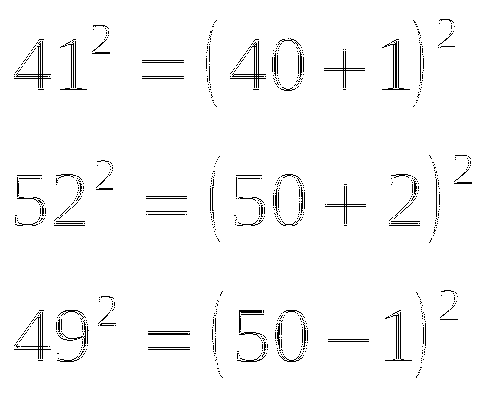
8. Дополнительное задание.

Дидактический материал стр.40 №2 таблица

9. Домашнее задание и его инструктаж.

Параграф 2 стр.65, правила,

№245 (I столбец)

№248 (I столбец)

10. Итог урока