Урок по теме 'Сфера. Уравнение сферы' (11 класс)

Тема: Сфера. Уравнение сферы.

Цель урока: Сформировать на уроке понятие и определение сферы, шара и их элементов, вывести уравнение сферы в заданной прямоугольной системе координат, формировать навык решения задач по данной теме.

Цели урока:

Образовательные: Сформировать на уроке понятие и определение сферы, шара и их элементов, вывести уравнение сферы в заданной прямоугольной системе координат, формировать навык решения задач по данной теме.

Развивающие: развивать логическое мышление, пространственное восприятие, математически грамотную речь.

Воспитательные: совершенствовать навыки самостоятельной работы, воспитывать внимание, аккуратность.

Ход урока

1. Организационный момент. Анализ результатов контрольной работы.

2. Актуализация:

А) на доске изображена окружность

Вопросы:

• Как называется линия изображенная на плоскости?

• Вспомните определение окружности. - Окружность-множество точек плоскости, равноудаленных от данной точки.

• Как называются элементы окружности? - Данная точка центр, отрезок, соединяющий центр с любой точкой окружности радиус, отрезок, соединяющий любые две точки окружности и проходящий через центр называется диаметр.

• Как называется часть плоскости ограниченная окружностью?- Круг.

• Дайте определение круга. - Круг - это часть плоскости, ограниченная окружностью.

Б) Вспомните название уравнений, записанных на доске

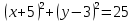
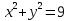
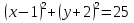
• Общий вид уравнения окружности.

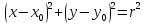, О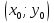

В) докажите, что данное уравнение является уравнением окружности:

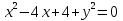
Чему равен радиус и назовите координаты центра.

Г) Принадлежит ли точка М(2;2) данной окружности?

• Что изучает стереометрия? - Стереометрия изучает свойства фигур в пространстве

• Как вы думаете, существует ли поверхность, состоящая из точек пространства, равноудаленных от данной точки? - Да

• Такая поверхность называется сферой.

3. Объяснение нового материала

Итак, тема сегодняшнего урока Сфера.

Запишите тему сегодняшнего урока в тетрадях.

Цели: Я уверена, что вы неоднократно встречались в жизни не только со сферой, но и с шаром. Сегодня на уроке мы с вами сформулируем определения этих пространственных фигур, их элементов и выведем уравнение сферы .

• Какая геометрическая фигура у вас ассоциируется со сферой? (окружность).

• Как бы вы сформулировали определение сферы? - Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

• Привести примеры окружающей обстановки, дающей представление о сфере.

• Как называется данная точка? - центр сферы

• Как называется данное расстояние? - радиус сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы.

Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром.

• А что такое шар? - Тело, ограниченное сферой, называется шаром.

• Чем он отличается от сферы? Давайте разберемся в этом вопросе, а для этого воспользуемся презентацией. - Шар содержит все точки пространства, которые расположены от точки О на расстоянии, не превышающем R, и не содержит других точек.

• Можно ли сферу и шар отнести к телам вращения? - Сфера может быть получена вращением полуокружности вокруг ее диаметра, а шар - вращением полукруга вокруг его диаметра.

4. Первичное закрепление: №573, 574(а)

5. Уравнение сферы:

Задание: Вывести уравнение сферы с центром в точке С(x₀;y₀;z₀) радиуса R, используя формулу расстояния между двумя точками с заданными координатами.

1. Найдите расстояние от произвольной точки М (x;y;z) до С(x₀;y₀;z₀)

2. Почему мы находим именно это расстояние? - так как это R

3. Формула для нахождения расстояния между двумя точками в пространстве?

4. Если точка М лежит на сфере, то МС = R.

Вывод: 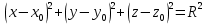уравнение сферы.

6. Закрепление изученного материала

Устно (слайд)

№ 577(а), 579 (а,г)

7. Самостоятельная работа:

8. Подведение итогов:

Итак, что сегодня нового мы узнали на уроке?

• Определение сферы

• Определение шара

• Определение элементов сферы и шара

• Как можно получить сферу и шар вращением

• Уравнение сферы

9. Задание на дом: