Дополнительный материал к урокам математики в 6 классе Аликвотные дроби

ОТДЕЛ ОБРАЗОВАНИЯ

АДМИНИСТРАЦИИ ПЕТРОВСКОГО РАЙОНА

ГОРОДА ДОНЕЦКА

ДОШ І-ІІІ СТУПЕНЕЙ №111

Аликвотные дроби

ПОДГОТОВИЛА

учитель математики ДОШ №111

Кулиш Л.Н.

г. Донецк-2016год

1.Введение

Необходимость в дробных числах возникла в результате практической деятельности человека. Потребность в нахождении долей единицы появилась наших предков при дележе добычи после охоты. Второй существенной причиной появления дробных чисел следует считать измерение величин при помощи выбранной единицы измерения.

Первой дробью, с которой познакомились люди, была половина. Хотя названия всех следующих дробей связаны с названиями их знаменателей (три - «треть», четыре - «четверть» и т. д.), для половины это не так - ее название во всех языках не имеет ничего общего со словом «два». Следующей дробью была треть.

Таким образом, первые дроби, с которыми нас знакомит история, это дроби вида - - так называемые единичные дроби или аликвотные (от лат. aliquot - «несколько»).

Единичные дроби встречаются в древнейших дошедших до нас математических текстах, составленных более 5000 лет тому назад, - древнеегипетских папирусах и вавилонских клинописных табличках. Египетская дробь - в математике сумма нескольких дробей вида (так называемых аликвотных дробей). Другими словами, каждая дробь суммы имеет числитель, равный единице, и знаменатель, представляющий собой натуральное число.

Пример: .

Египетская дробь представляет собой положительное рациональное число вида ; к примеру, египетская дробь, записанная выше, может быть записана в виде дроби 43/48. Можно показать, что каждое положительное рациональное число может быть представлено в виде египетской дроби. Сумма такого типа использовалась математиками, как определение, для дробей начиная со времён древнего Египта до средневековья.

Задачи с использованием в решении аликвотных дробей составляют обширный класс нестандартных задач. Сюда относятся, прежде, всего, задачи, в которых требуется разделить какие-либо ресурсы на несколько частей с наименьшим количеством действий для этого.

Цель исследования:

• Выяснить, какое значение имеют аликвотные дроби в нашей жизни

Задачи исследования:

• Узнать происхождение аликвотных дробей.

• Рассмотреть основные операции с аликвотными дробями.

• Составлять и решать задачи практического содержания.

Происхождение аликвотных дробей.

Тема «Аликвотные дроби» является интересной темой для исследования дробей. Столкнувшись с этим термином впервые, понимаешь, почему в Древнем Египте математики «настоящими» дробями считали только аликвотные дроби.

Итак, Египтяне все дроби записывали как суммы долей, то есть дробей вида 1/n. Например: 8/15=1/3+1/5. Дроби 1/n ( где n - натуральные число ), которым египтяне отдавали предпочтение, в современной математике именуются аликвотными ( от латинского aliguot- " несколько''). То есть аликвотными дробями называются дроби с числителем 1. И даже сами аликвотные дроби они часто стремились представить в виде суммы меньших аликвотных дробей. Например,

1/2=1/3+1/6, 1/4=1/5+1/20

Египтяне ставили иероглиф «Глаз Хора»

Такие дроби использовались вместе с другими формами записи египетских дробей для того, чтобы поделить «хекат», основную меру объёма в Древнем Египте, т.е.аликвотные дроби нужны были египтянам в практических целях.

Поясним это примером. Рассмотрим такую задачу: «Разделить 7 хлебов между 8 людьми».

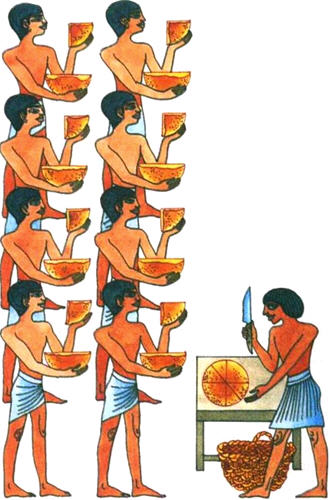
Очевидно, каждый должен получить одного хлеба. Современный школьник скорее всего решал бы задачу так: надо разрезать каждый хлеб на 8 равных частей и каждому человеку дать по одной части от каждого хлеба. А вот как эта задача решена на папирусе Райнда - это древнеегипетский математический текст, переписанный около 1650 г. до н.э. писцом Ахмесом.

Поскольку . Следовательно, каждому человеку нужно дать по половине, четверти и восьмушке хлеба. Теперь ясно, что надо 4 хлеба разрезать пополам, 2 хлеба на 4 части и только один хлеб - на 8 частей. И если нашему школьнику пришлось бы сделать 49 разрезов, то Ахмесу - всего 17, т.е. египетский способ почти в 3 раза экономичнее.

Если разрезать каждый хлеб на 8 частей, придется провести 49 разрезов. А по-египетски эта задача решалась так: 7/8= 1/2 +1/4 +1/8. Значит, каждому человеку дать полхлеба, четверть хлеба и восьмушку хлеба. Придется сделать почти в три раза меньше разрезов.

Египетские дроби продолжались использоваться в древней Греции и впоследствии математиками всего мира до средних веков, несмотря на имеющиеся к ним замечания древних математиков . К примеру, Клавдий Птолемей говорил о неудобстве использования египетских дробей по сравнению с Вавилонской системой(позиционная система исчисления)

Важную работу по исследованию египетских дробей провёл математик XIII века Фибоначчи в своём труде «Liber Abaci» - это вычисления, использующие десятичные и обычные дроби, вытеснившие со временем египетские дроби. Фибоначчи использовал сложную запись дробей, включавшую запись чисел со смешанным основанием и запись в виде сумм дробей, часто использовались и египетские дроби. Также в книге были приведены алгоритмы перевода из обычных дробей в египетские.

2.2 Основные операции над аликвотными дробями

Чтобы представить какое либо число в виде суммы аликвотных дробей, порой приходится проявлять, незаурядную изобретательность. Скажем, число 2/43 выражается так: 2/43= 1/42 +1/86 +1/129 +1/301.Производить арифметические действия над числами, раскладывая их в сумму долей единицы, очень неудобно.

Поэтому в процессе решения задач для разложения аликвотных дробей в виде суммы меньших аликвотных дробей возникла идея систематизировать разложение дробей в виде формулы. Эта формула действует, если требуется разложение аликвотной дроби на две аликвотные дроби.

Формула выглядит следующим образом:

1/n=(1/(n+1)) +(1/n*(n+1))

Примеры разложения дробей:

1/3=1/(3+1)+1/3*(3+1)=1/4 +1/12;

1/5=1/(5+1)+1/5*(5+1)=1/6 +1/30;

1/8=1/(8+1)+1/8*(8+1)=1/9+ 1/72.

Но если преобразовать нашу формулу, то получим следующее полезное равенство:

1/(n*(n+1))=1/n -1/(n+1)

1/6=1/(2*3)=1/2 -1/3

½=1/(1*2)=1/1 -1/2

Т.е. аликвотную дробь можно представить разностью двух аликвотных дробей, или разность двух аликвотных, знаменателями которых являются последовательные числа равна их произведению.

Вернемся к формуле и докажем это равенство:

1/n=(1/(n+1)) +(1/n*(n+1))

(1/(n+1)) +(1/n*(n+1)) , приведя дроби к общему знаменателю, получаем:

( n+1 )/((n+1)*n) после сокращения получаем:

1/n.

Итак, получается, что 1/n=1/n. Наша формула верна.

Но мы пойдем дальше, и на основании разности аликвотных дробей решим, на первый взгляд, трудноразрешимую для обычного человека задачу:

1/2+1/(2*3)+1/(3*4)+1/(4*5)+…….+1/(19*20) =????

Воспользуемся нашей формулой для разложения аликвотной дроби в виде разности:

½=1/(1*2)=1/1 -1/2

1/6=1/(2*3)=1/2-1/3

1/12=1/(3*4)=1/3-1/4

1/20=1/(4*5)=1/4-1/5 и т.д.

Подставив, уже разложенные выражения в наш пример, получаем:

1/1-1/2+1/2-1/3+1/3-1/4+1/4-1/5……..+1/19-1/19-1/20=1/1-1/20=19/20.

Мы представили формулу, как удобство при разложении аликвотной дроби на 2 слагаемых. При разложении 1 на два слагаемых получается:

1=1/2+1/2 (Наша формула действует!). Чтобы разложить 1 на 3 слагаемых, мы возьмем одну аликвотную дробь и по формуле разложим ее еще на две аликвотные дроби:

½=1/3+1/6 =½=1/3+1/6 => 1=1/2+1/3+1/6;

Чтобы разделить на 4 слагаемых, делим еще одну дробь на две аликвотные дроби:

1/3=1/4+1/12 => 1=1/2+1/4+1/12+1/6;

На 5 слагаемых: 1/6=1/7+1/42 => 1=1/2+1/4+1/12+1/7+1/42.

2.3 Решение задач

2.3.1.Представить число 1 в виде сумм различных аликвотных дробей

А) трех слагаемых

1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6

Б) четырех слагаемых

1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6=1/2+1/3+(1/7+1/42)= 1/2+1/3+1/7+1/42

B) 5-и слагаемых

1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6=1/2+1/3+(1/7+1/42)=

1/2+1/3+1/7+1/42=1/2+(1/4+1/12) +1/7+1/42=

1/2+1/4+1/12 +1/7+1/42

Задача

Чтобы узнать в каком году в Донецке будет проводиться чемпионат Европы по футболу нужно сумму аликвотных дробей

1/(1*2)+1/(2*3)+1/(3*4)+…+1/(2012*2013) умножить на 2013.

Решение :

1/(1*2)+1/(2*3)+1/(3*4)+…+1/(2012*2013)=2012/2013

2012/2013 * 2013 = 2012

Ответ : Чемпионат Европы будет проводиться в 2012 году.

Заключение.

Таким образом, при разработке данной темы, мы узнали, что первыми дробями, которыми оперировали люди, были аликвотные дроби. Выяснили, что каждое рациональное число вида a/b может быть разложено на единичные дроби.

Задачи с использованием аликвотных дробей составляют обширный класс нестандартных задач. Аликвотные дроби используются тогда, когда требуется что-то разделить на несколько частей с наименьшим количеством действий для этого.

Разложение дробей на две аликвотные дроби систематизировали в виде формулы, преобразовав которую, легко решили олимпиадные задачи по математике разных лет.

Решив проблему разложения аликвотных дробей на две аликвотные дроби, мы пришли к выводу, что разложение на три, четыре, пять и т.д. аликвотных дробей можно произвести, разложив одно из слагаемых на две дроби, следующее слагаемое еще на две аликвотные дроби и т.д.

Таким образом, аликвотные дроби (с числителем 1) долгое время были единственными дробями, с которыми как-то умел оперировать человек, а правила действий с произвольными дробями разработаны «сравнительно недавно».

В современной математике вместо египетских дробей используются простые и десятичные дроби, однако египетские дроби продолжают изучаться в теории чисел и истории математики.

</

4.Используемая литература:

1. Энциклопедический словарь юного математика для среднего и старшего школьного возраста. М.: Педагогика,1989.

2. Левитас Г. Г. Нестандартные задачи по математике.- М.: ИЛЕКСА,2007.

3. Баженов И.И., Порошкин А.Г. и др. Задачи для школьных математических кружков. Сыктывкар, 1994.

4. Гаврилова Т. Д. «Занимательная математика». 5-11класс. Волгоград: Учитель, 2008.

5. Фарков А. В. Математические олимпиады в школе. 5-11класс. - М.: Айрис-пресс, 2005.