- Учителю
- Урок в 11 классе по теме «Разнообразие способов решения тригонометрических уравнений вида аrcsin x+ b cos x=c»
Урок в 11 классе по теме «Разнообразие способов решения тригонометрических уравнений вида аrcsin x+ b cos x=c»















 План-конспект элективного занятия по алгебре и началом анализа в 11 классе. Повторение. 2 часа.
План-конспект элективного занятия по алгебре и началом анализа в 11 классе. Повторение. 2 часа.
Тема: «Разнообразие способов решения тригонометрических уравнений вида
аrcsin x+ b cos x=c»
Работа учителя МКОУ ГСШ Капустиной Н.П.
Урок в 11 классе (повторение)
Тема: Различные методы решения одного тригонометрического вида
arcsin x+b cos x=c
Цели урока:
-
Образовательные
-решение одного тригонометрического уравнения sinx+ cosx=1всеми способами и выбрать наиболее рациональный
-Указать внешние признаки, по которым устанавливается способ решения.
-
Развивающие
-Развить творческую и мыслительную деятельность учащихся через решение разнотипных заданий
-Умение анализировать; сравнивать математические объекты;
-Способствовать развитию интеллектуальных качеств (самостоятельность мышления, способность к переключению, общению, обобщению);
-Формировать навыки самостоятельной и коллективной работы.
-
Воспитательные
-Привить учащимся интерес к предмету через решение задач;
-Способствовать выработке умения обобщать изучаемые факты;
-Формировать умение ясно и четко излагать свои мысли и грамотно выполнять математические задачи, воспитывать веру в свои силы.
Ход урока.
-
Устная работа.
Не решая уравнений, сообщите каким способом, следовало бы решать каждое уравнение.
-
2cos²3x+sin 3x-1=0
cos²3x=1-sin²3x
2sin²3x-sin3x-1=0
(алгебраический способ)
-
7соs²x-sinxcosx+4 sin²x=5; Однородное уравнение
7cоs² x-sin x cos x+4 sin²x=5(sin²x+cos²x);
-
2tgx-3=2 ctgx; алгебраический способ
Ctg x= 1/tg x
-
3 sinx +4 cosx=2; введение вспомогательного угла уравнение видаacosx+bsinx=c
-
Cos 3x *cos 2x = sin 3x*sin2x
Косинус суммы
-
3sin²x + sin 2x =3
Прийти к однородному уравнению
Sin2x=2sin x cos x
3=3cos²x+ 3 sin²x
-
Cosx - cos 3x= sin 2xразность косинусов
-2 sin 2x *sin(-x)=sin 2x
Sin2x( 2 sinx-1)=0 произведение равно нулю
-
Сos 2x=
 (cos x- sin x)
(cos x- sin x)
П=0
cos²x-sin²x= (cos x-sin x)
(cos x-sin x)
(cos x - sin x) (cosx+sin x+2)=0
-
Новый материал (Слово учителя).
Разнообразие способов решения тригонометрических уравнений разберем на примере уравнения sinx + cosx =1
Замечание
1 .При решении могут получаться внешне различные ответы.
2. если решение получено в виде нескольких формул, то необходимо проверить, не повторяют ли эти формулы одни и те же значения х.
Перед вами различные способы ( оформить на доске) решения этого уравнения
-
Введение вспомогательного угла.
-
Универсальная подставка sinL=

X=П+2Пn, n€ Z
-
Сведение к однородному уравнению 2-ой степени, т.е.
-
Преобразование суммы в произведение (формулы приведения).
-
Возведение в квадрат обеих частей уравнения.
-
Разложение левой части на множители.
-
Замена переменных.
-
Графический метод.
-
Метод оценивания.
-
Замена соsx=±
 .
.
II B
Рассмотрим общий способ решения уравнения asin x + b cos x=c, который вызывает серьезные затруднения при решении.
Способ введения вспомогательного угла
a sin x + cos x=c
A =
Cos f= , sin f=
, sin f=
a sin x + b cos x= A ∙ sin x+ A
sin x+ A cos x=A sin (x+f)
cos x=A sin (x+f)
или a sin x + b cos x=A cos (x-f)
Значит,
Sin(x+f)= , где
, где 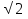
IIC
Решить уравнение (самостоятельно) с проверкой у доски
1 способ. Метод введения вспомогательного аргумента
Решение. Cos x + sin x=1
A=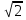 =
= . (разделим обе части на
. (разделим обе части на 
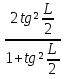 sinx=
sinx=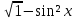
Заметим, что 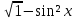 =сos
=сos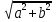 = sin
= sin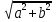
cos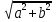 cos x +sin
cos x +sin 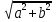 sin x=
sin x=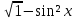
cos(x-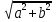 ) =
) =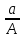 ,
,
x-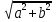 =
=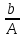 , n€Z/
, n€Z/
x1=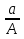
x2=2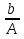
Множество решений уравнения изобразим на числовой окружности, отметив ключевые точки
y 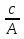
x
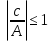
Ответ: 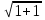
Х=2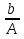
2 способ Универсальный ( Этот способ применяют лишь тогда, когда не видно путей решения)
Пусть 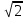 , nj
, nj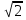 , то
, то 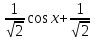 , cosx=
, cosx=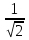 , причем tg
, причем tg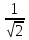 не существует, если cos
не существует, если cos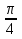 ,
,
т.е. х=П+2Пn, n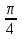
Выполнив замену, получаем
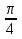 1+t2
1+t2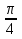 0, то
0, то
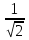 ,
,
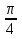 ,
,
2t(1-t)=0
t=0 или 1-t=0
t=1
Тогда,
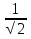 или
или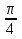
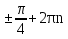
X=2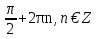 ; х=
; х=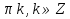
y 
x
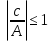
Ответ: 2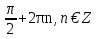 ; х=
; х=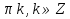
3 способ. Решение используя формулы двойного аргумента для 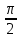 и
и и основное тригонометрическое тождество получим:
и основное тригонометрическое тождество получим:
2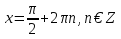
2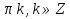 =0 ( разделим 2
=0 ( разделим 2 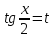 0
0 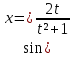 =0 не является решением)
=0 не является решением)
tg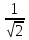 -tg2
-tg2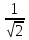 =0
=0
Значит, tg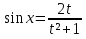 или g
или g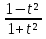 ,
, 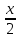
X=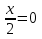
y 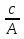
x
2π
Ответ: х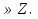
X=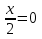
4 способ. ( Использование тригонометрии)
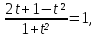 (Формула приведения)
(Формула приведения)
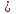 ;
;
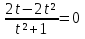 ;
;
2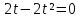 =1 ;
=1 ;
2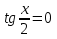
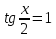 ;
;
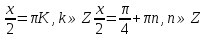 ;
;
Х-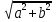 =±
=±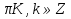
y 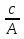
x
2π
Ответ: х=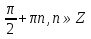
X=2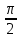
5 способ. Возведение в квадрат обеих частей.
(Замечание:При возведение в квадрат получаем неравносильное преобразование, поэтому полученные корни нужно проверить! )

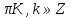
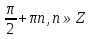
1+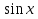
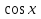
X=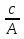 n, n
n, n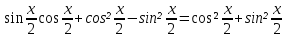 Z
Z
N=0, x=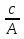 -решение y
-решение y 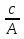
x
2π
N=1, x=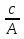 -решение
-решение
N=2, x=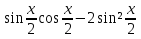 - является решением
- является решением
N=3, x=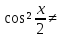 - не является решением
- не является решением
Ответ: х=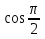
X=2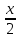
6 способ. Разложение на множители левой части
Решение  ;
;
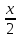 ;
;
2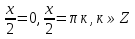 ;
;
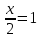 ;
;
2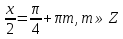 или
или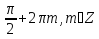 однородное уравнениеcos
однородное уравнениеcos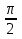
X=2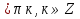 1-tg
1-tg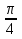
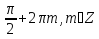 +
+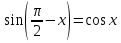
X=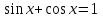
Ответ:X=2πn,n∈Z
7 способ.X=π/2+2πK,K∈Z7 способ. Замена переменных.
Решение. Пусть 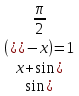 ,
, 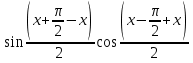 ,
,
То 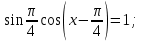
-
a+b=1
-
Добавим к нему основное тригонометрическое тождество.
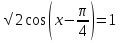
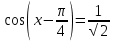
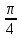 или
или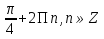
Ответ: х=2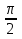 , x=
, x=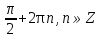
8 способ.графический sinx+ cosx=1.
Построим графики двух функций
y=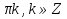 , y=1-
, y=1-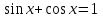
Ответ: х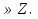
X=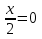
9 способ. Метод оценивания.
sin x+ cos x=1.
Решение.
Рассмотрим четыре случая.
а) Если х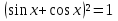 чет., то 0
чет., то 0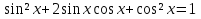 , значит
, значит
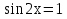 ,
, 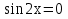 ,
,
То 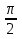 ,
, 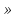
б) Если х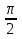 чет., то 0
чет., то 0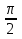 -1
-1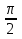
и 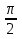
в) Если х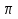 чет.,
чет., 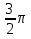
Значит 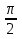
г) Если х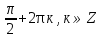
1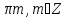
Значит 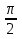
Итак, решения могут быть только в граничных точках (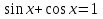
Проверим каждую.
Х=0, х=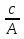 , х=П, х=
, х=П, х=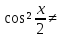
Ответ: корни х=2Пк, к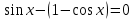 или х=
или х=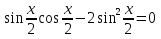
10 способ. Замена 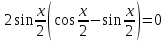
Решение.
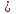
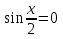 (иррациональное уравнение)
(иррациональное уравнение)
1-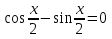
1-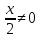
-2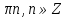
-2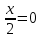
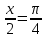 или
или 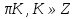
Х=ПM, m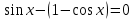 x=
x=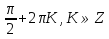
X=2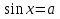
Ответ: x=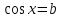
Х=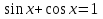
Вывод. Видим, что одно уравнение можем решить различными способами. При этом простота и красота зависит от способа решения.
Выбор наиболее целесообразных методов решения достигается практикой!
-
Задание на дом.
Решите уравнения любыми разными способами.
А) 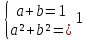
Б)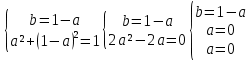
В)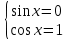
Оценки за работу.