Урок алгебры в 10 классе по теме

Урок алгебры в 10 классе по теме "Решение неравенств методом интервалов".

Цели урока:

Образовательные:

• проконтролировать знания учащихся по усвоению алгоритма решения неравенств методом интервалов;

• выработать умения и навыки по их самостоятельному применению при решении упражнений по образцу, в сходной, измененной ситуации.

• Повторить основные приемы преобразования и решения рациональных и дробно-рациональных неравенств методом интервалов, акцентировать внимание учащихся на поиске и прогнозировании ошибок.

Развивающие:

• продолжить развитие умения решать более сложные неравенства;

• обеспечить развитие математической речи, самооценки, умение работать во времени.

Воспитательные:

• создать условия для развития коммуникативных навыков;

• умения работать в парах; побуждать учащихся к самоанализу своей деятельности,умения выслушивать ответы одноклассников.

Оборудование:

• Компьютер.

• Экран.

• Магнитная доска.

Дидактические материалы: презентация к уроку, плакаты -шаги схемы "Обобщенный метод интервалов решения неравенств "; карточки для творческой работы в парах, для самостоятельной работы и для тестирования.

Ход урока

1. Организация начала урока. (1 мин.)

- Здравствуйте, ребята. Запишите число и тему урока "Метод интервалов решения неравенств". Почти все неравенства школьного курса можно решить методом интервалов. Сегодня мы ответим на вопросы : Какие неравенства мы можем решать методом интервалов? Какие преобразования необходимо сделать , чтобы привести неравенство к виду неравенства , решаемого методом интервалов. И составим схему обобщенного метода интервалов решения неравенств.

Познакомьтесь с планом урока.

План урока

• Проверка домашнего задания.

• Беседа. Обобщение теоретических знаний и составление схемы обобщенного метода интервалов.

• Применение знаний. Индивидуальная работа и работа в парах.

• Применение метода интервалов при решении задач.

• Самостоятельная работа.

• Итог урока. Рефлексия.

• Домашнее задание.

2. Проверка выполнения домашнего задания. (5 мин.)

На экран выносятся решения неравенств с ошибками.(Приложение 1). Учащимся предлагается сверить свою работу с записью на экране и найти ошибку. Вызванный ученик аргументированно объясняет решение, затем отвечает следующий. По готовым ответам к домашним заданиям исправить свои ошибки.( Приложение 2).

3. Беседа . Обобщенный метод интервалов решения неравенств.( 7 мин)

На доске выписаны несколько неравенств : 1. (х-8)(х+1)(х-2)>0

2. (6-х)(9+х)(х-3)<0

3. (х-5)²(х+4)³х<0

4. >0

5. х²+2х-15<0

6. (2х+1)(3х-6)(х-5)<0

Вопросы: 1.В чем заключается метод интервалов решения неравенств? Какого вида неравенства решают этим методом?

+2. На примере неравенства (1) расскажите , как решают неравенства методом интервалов.

3. На примере остальных неравенств расскажите , какие преобразования необходимо сделать, чтобы привести левую часть неравенств к виду (х-х1)(х-х2)(х-х3)…(х-хп) ?

4. На примере неравенства (3) расскажите план решения неравенств с учетом кратности корней. Ответ сопровождается составлением схемы обобщенного метода интервалов решения неравенств на магнитной доске.

1 шаг. Приравнять левую часть неравенства к нулю и решить уравнение.

2 шаг. Отметить на числовой прямой корни уравнения

3 шаг. В правом крайнем интервале поставить знак «+» , а дальше пользуясь свойством чередования, расставить знаки в остальных интервалах, меняя знак при переходе через корень нечетной степени, и сохранить знак при переходе через корень четной степени.

4 шаг. Записать ответ в соответствии со знаком неравенства.

4. Парная работа. ( 6 мин)

1 задание( творческое). Составить неравенство по готовой картинке и предупредить возможные ошибки.

( Приложение 3).

По мере готовности пары выходят к доске .

2 задание . Решить тест. (Приложение4) Взаимопроверка по готовым ответам. Правильные ответы проектируются на экран.

(Приложение 5)

5.Применение метода интервалов.( 10 мин).

1.Решить задачу. Длина прямоугольника на 3 см больше ширины. Какую длину должен иметь прямоугольник, чтобы его площадь была меньше 28 см²?

Решение:

Пусть длина прямоугольника х см ,х>0, тогда его ширина (х-3)см. S=х(х-3) см²

Зная, что S<28 см² , составим и решим неравенство:

х(х-3)<28

х²-3х-28<0 х²-3х-28=0

(х+4)(х-7)<0 х1+х2=3

+ - + х1*х2=-28 , х1=-4 х2=7

────о───о────›

-4 7

Выбираем промежуток (-4;7) и учитывая условия х>0 и х-3>0, получаем (3;7).

Значит, длина прямоугольника должна быть больше 3 , но меньше 7.

2.Найти область определения функции у=.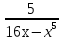

Решение:

16х-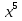>0

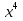х(16-)>0

х(4-х²)(4+х²)>0

х(2-х)(2+х)(4+х²)>0 Выражение 4+х²>0 при любых значениях х

х(х-2)(х+2)<0

Х1=0 Х2=2 Х3=-2

- + - +

────о──────о──────о───────›

-2 0 2

Ответ: D(y)=(-∞;-2)(0;2)

6. Самостоятельная работа. ( 12 мин) (Приложение 6)

7.Итог урока. Прокомментировать оценки учащихся.( 2 мин)

8. Рефлексия. Заполнить табличку. ( 2 мин)

1. Сегодня на уроке было интересно ___________________________________

2. Сегодня на уроке я научился _______________________________________

3. Сегодня на уроке мне показалось важным ___________________________

8. Домашнее задание. № 2.77(е), 2.78 (в,г,д)

Приложение 1. Проверка домашнего задания.

№ 2.71 (в) №2.67 (з)

(х+3)(х+4)²(х+5)³<0 (х²+3х)(х²-16)>0

Х1=-3 Х2=-4 Х3=-5 Х(Х+3)(Х-4)(Х+4)>0

- + - + Х1=0 Х2=3 Х3=4 Х4=-4

────о─────о─────о─────› + - + - +

-5 -4 -3 ─────о────о────о────о──────›

(-∞;-5)U(-4;-3) -4 0 3 4

(-∞;-4)U(0;3)U(4;+∞)

№2.76 (в) №2.77(г)

>1 <0

-1>0 (х+2)²(х+1)(х-3)>0

>0 Х1=-2 Х2=-1 Х3=3

>0 Х1=2 Х2=-1 + + - +

+ - + ────о────о────о──────›

───о────о─────› -2 -1 3

-1 2 (-∞;-2)U(-2;-1)U(3;+∞)

(-∞;-1)U(2;+∞ )

Приложение 2. Правильные ответы .

№2.71 (в) (-5;-4)U(-4;-3)

№2.67(з) (-∞;-4)U(-3;0)U(4;+∞)

№2.76(в) (-∞;-1)U(4;+∞)

№2.77(г) (-1;3)

Приложение 3.

1 пара

Составьте неравенство по картинке . Выделены промежутки-ответы. Предупредите о возможных ошибках.

+ + - +

─────о────о───о───›

-1 0 4

(-∞;-1)U(-1;0)U(4;+∞)

2 пара

Составьте неравенство по картинке . Выделены промежутки-ответы. Предупредите о возможных ошибках.

+ - + - +

───о───о───о───о───›

-2 -1 5 7

(-2;-1)U(5;7)

3 пара

Составьте неравенство по картинке . Выделены промежутки-ответы. Предупредите о возможных ошибках.

+ - - +

─────о────о────о─────›

-5 -4,5 3

(-∞;-5)U(3;+∞)

4 пара

Составьте неравенство по картинке . Выделены промежутки-ответы. Предупредите о возможных ошибках.

+ - + +

─────о─────о─────о─────────›

-6 1 8

(-6;1)

Приложение 4 Т Е С Т

Вариант 1

Метод интервалов решения неравенств.

Выберите один правильный по вашему мнению ответ и впишите в бланк ответов . Бланк расположен под тестом.

1.Укажите наибольшее целое число, принадлежащее промежутку (-7; -1,8)

А -1

В -7

С -2

2.Какой из промежутков является решением неравенства х-5>0 ?

А (5;+∞)

В (-5;5)

С (-∞;5)

3.Найдите корни уравнения (х-1)(Х-2)(х+3)=0

А 1;2;3

В 1;2;-3

С -1;-2;-3

4.Решением какого неравенства является промежуток (-3;2)?

А (х+3)(х+2)<0

В (х+3)(х-2)<0

С (х-3)(х+2)>0

5.Решите неравенство х16

А (-∞;4)

В (-4;4)

С (4;+∞)

Бланк ответов .

№ задания

1 задание

2задание

3 задание

4 задание

5 задание

Ваш ответ

За каждый правильный ответ- 1 балл.

Количество баллов:_______

Т Е С Т

Вариант 2

Метод интервалов решения неравенств.

Выберите один правильный по вашему мнению ответ и впишите в бланк ответов . Бланк расположен под тестом.

1.Укажите наименьшее целое число, принадлежащее промежутку (-5,3; 2)

А -5

В 2

С -4

2.Какой из промежутков является решением неравенства х+5>0 ?

А (-5;5)

В (-5;+∞)

С (-∞;5)

3.Найдите корни уравнения (х+1)(Х-2)(х-3)=0

А 1;2;3

В -1;2;3

С -1;-2;-3

4.Решением какого неравенства является промежуток (-2;3)?

А (х+3)(х+2)<0

В (х+3)(х-2)>0

С (х-3)(х+2)<0

5.Решите неравенство х16

А (-∞;-4)U(4;+∞)

В (-4;4)

С (4;+∞)

Бланк ответов .

№ задания

1 задание

2задание

3 задание

4 задание

5 задание

Ваш ответ

За каждый правильный ответ- 1 балл.

Количество баллов:_______

Приложение 5. Проверка теста.

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Вариант 1

С

А

В

В

В

Вариант 2

А

В

В

С

А

Приложение 6. Самостоятельная работа.

Вариант А1 Вариант А2

1.Решите неравенство: 1. Решите неравенство:

а)(х+2)(х-3)(х+1)>0 а) (х-2)(х+3)(х-1)<0

б) х(4-х)(х-2)>0 б)(3-х)(х+2)х>0

в) (х-1)²(х-4)³(х+5)<0 в) (х+4)²(х-5)(х+3)³<0

2.Найти область определения 2.Найти область определения

функции у= функции у=