- Учителю
- Рабочая программа по математике 8 класс
Рабочая программа по математике 8 класс
| Рассмотрено на ШМО «Математика» Руководитель_________ /Лапина О.Д./ От « »_______2014___ г | Согласовано Зам директора по УВР _______ /Жильцова И.В./ от « » ______2014___ г. | «Утверждаю» Директор МБОУ«Курьинская сош» им. М.Т.Калашникова __________ /Лёгоньких JI.H./ Приказ № _______ от « » _______2014___ г
|
.
.
Администрация Курьинского района Алтайского края
Муниципальное бюджетное образовательное учреждение
«Курьинская средняя общеобразовательная школа» имени М.Т. Калашникова.
Рабочая программа
по математике для 8 класса
по учебному курсу «Алгебра», «Геометрия»
базовый уровень
на 2014-2015 учебный год
Образовательная область: Математика
Сроки реализации: 2014-2015 учебный год
Разработчик: Лапина Ольга Дмитриевна,
учитель математики, высшей квалификационной категории
с. Курья
2014 год
Пояснительная записка
Данная рабочая программа ориентирована на учащихся 8 класса и реализуется на основе следующих документов:
-
Федерального компонента государственного образовательного стандарта основного общего образования
-
Примерной программы основного общего образования по математике
-
Базисного учебного плана общеобразовательных учреждений Российской Федерации (2014г)
-
Авторская программа. Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель: Бурмистрова Т. А. - Москва «Просвещение» 2010 г.
-
Программы общеобразовательных учреждений. Геометрия. 7-9 классы. Составитель: Бурмистрова Т. А. - Москва «Просвещение» 2009 г.
-
Основной общеобразовательной программы МБОУ «Курьинская средняя общеобразовательная школа» им М.Т. Калашникова.
Изучение курса в 8 классе направлено на достижение следующих целей:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
В ходе освоения содержания курса «Математика 8» ставятся задачи:
-
изучение выражений и действий с ними, выработать умения выполнять тождественные преобразования выражений, выражений содержащих квадратные корни и степени с целым показателем;
-
расширить аппарат уравнений через формирование умений решать квадратные и простейшие рациональные уравнения;
-
выработать умения решать линейные неравенства с одной переменной и их системы;
-
изучение функций и их графиков и использование графиков для описания процессов реальной жизни;
-
получить представления об особенностях выводов и прогнозов, носящий вероятностный характер;
-
изучить понятие вектора;
-
расширить понятие треугольника;
-
ввести декартовы координаты на плоскости;
-
сформировать понятие четырехугольника.
Обоснование выбора авторской программы:
Предлагаемая программа по математике составлена в соответствии с требованиями федерального компонента государственного образовательного стандарта основного общего образования по математике. Они позволяют получить представление о целях и содержании обучения математике в 7-9 классах, в рамках обучения по учебникам, выпускаемых издательством «Просвещение». Программа соответствует учебнику: Алгебра. 8 класс: учебник для общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк и др.; под ред. С. А. Теляковского. - М.: Просвещение, 2009. Геометрия 7-9 класс: учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И Юдина. - М.: Просвещение, 2009. - 384 с.
Авторская программа взята без изменений.
Место предмета в учебном плане:
Согласно федеральному базисному учебному плану на изучение математики в 8 классе отводится 175 часов (в неделю 5 часов). Из них алгебра - 105 часа, геометрия - 70 часов по I варианту (алгебра: 3 часа в неделю, геометрия: 2 часа в неделю).
Виды и формы контроля:
В курсе математика 8 класса предусмотрено 15 контрольных работ, которые проводятся после изучения каждой темы, а в некоторых главах проводится более одной контрольной работы.
Критерии оценивания письменных контрольных работ учащихся
Отметка «5» ставится, если:
-
работа выполнена полностью;
-
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
-
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
-
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
-
допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Отметка «3» ставится, если:
-
допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
-
допущены существенные ошибки, показавшие, что учащийся не владеет
обязательными умениями по данной теме в полной мере.
Содержание обучения курса алгебры.
-
Рациональные дроби.
Рациональная дробь. Основное свойство дроби, сокращение дробей.
Тождественные преобразования рациональных выражений. Функция y=![]() и ее график.
и ее график.
Основная цель - выработать умения выполнять тождественные преобразования рациональн6ых выражений.
Так как действия с рациональными дробями существенным образом опираются на действия с многочленами, то в начале темы необходимо повторить с учащимися преобразование целых выражений.
Главное место в данной теме занимают алгоритмы действий с дробями. Учащиеся должны понимать, что сумма, разность, произведение и частное дробей всегда можно представить в виде дроби. Приобретаемые в данной теме умения выполнять сложение, вычитание, умножение и деление дробей являются опорными в преобразовании дробных выражений. Поэтому им следует уделять особое внимание. Нецелесообразно переходить к комбинированным заданиям на все действия с дробями прежде, чем будут усвоены основные алгоритмы. Задания на все действия с дробями не должны быть излишне громоздкими и трудоемкими.
При нахождении значений дробей даются задания на вычисления с помощью калькулятора. В данной теме расширяются сведения о статистических характеристиках. Вводится понятие среднего гармонического ряда положительных чисел.
Изучение темы завершается рассмотрением свойств графика функции y=![]()
-
Квадратные корни.
Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция y=![]() , ее свойства и график.
, ее свойства и график.
Основная цель - систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие о числе; выработать умения выполнять преобразования выражений, содержащих квадратные корни.
В данной теме учащиеся получают начальное представление о понятии действительного числа. С этой целью обобщаются известные учащимся сведения о рациональных числах. Для введения понятия иррационального числа используется интуитивное представление о том, что каждый отрезок имеет длину и потому каждой точке координатной прямой соответствует некоторое число. Показывается, что существуют точки, не имеющие рациональных абсцисс.
При введении понятия корня полезно ознакомить учащихся с нахождением корней с помощью калькулятора.
Основное внимание уделяется понятию арифметического квадратного корня и свойствам арифметических квадратных корней. Доказываются теоремы о корне из произведения и дроби, а также тождество ![]() 2=|a|, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида
2=|a|, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида ![]() ,
, ![]() . Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсе геометрии, алгебры и начал анализа.
. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсе геометрии, алгебры и начал анализа.
Продолжается работа по развитию функциональных представлений учащихся. Рассматриваются функция y=![]() , ее свойства и график. При изучении функции y=
, ее свойства и график. При изучении функции y=![]() показывается ее взаимосвязь с функцией y=x2, где x
показывается ее взаимосвязь с функцией y=x2, где x![]() .
.
-
Квадратные уравнения.
Квадратные уравнения. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
Основная цель - выработать умения решать квадратные уравнения и простейшие рациональные уравнения и применять их к решению задач.
В начале темы приводятся примеры решения неполных квадратных уравнений. Этот материал систематизируется. Рассматриваются алгоритмы решения неполных квадратных уравнений различного вида.
Основное внимание следует уделить решению уравнений вида ax2+ba+c=0, где a≠0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
Учащиеся овладевают способом решения дробных рациональных уравнений, который состоит в том, что решение таких уравнений сводится к решению соответствующих целых уравнений с последующим исключением посторонних корней.
Изучение данной темы позволяет существенно расширить аппарат уравнений, используемых для решения текстовых задач.
-
Неравенства.
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.
Основная цель - ознакомить учащихся с применением неравенств для оценки значений выражений, выработать умения решать линейные неравенства с одной переменной и их системы.
Свойства числовых неравенств составляют ту базу, на которой основано решение линейных неравенств с одной переменной. Теоремы о почленном сложении и умножении неравенств находят применение при выполнении простейших упражнений на оценку выражений по методу границ. Вводятся понятия абсолютной погрешности и точности приближения, относительной погрешности.
Умения проводить дедуктивные рассуждения получают развитие, как при доказательствах указанных теорем, так и при выполнении упражнений на доказательства неравенств.
В связи с решением линейных неравенств с одной переменной дается понятие о числовых промежутках, водятся соответствующие названия и обозначения. Рассмотрению систем неравенств с одной переменной предшествует ознакомление учащихся с понятиями пересечения и объединения множеств.
При решении неравенств используются свойства равносильных неравенств, которые разъясняются на конкретных примерах. Особое внимание следует уделить отработке умения решать простейшие неравенства вида ax>b, ax<b, остановившись специально на случае, когда a<0.
В этой теме рассматривается также решение систем двух линейных неравенств с одной переменной, в частности таких, которые записаны в виде двойных неравенств.
-
Степень с целым показателем. Элементы статистики.
Степень с целым показателем и ее свойства. Стандартный вид числа. Начальные сведения об организации статистических исследований. Основная цель - выработать умения применять свойства степени с целым показателем в вычислениях и преобразованиях, сформировать начальные представления о сборе и группировки статистических данных, их наглядной интерпретации.
В этой теме формируются свойства степени с целым показателем. Метод доказательства этих свойств показывается на примере умножения степеней с одинаковыми основаниями. Дается понятие о записи числа в стандартном виде. Приводятся примеры использования такой записи в физике, технике и других областях знаний.
Учащиеся получают начальные представления об организации статистических исследований. Они знакомятся с понятиями генеральной и выборочной совокупности. Приводятся примеры представления статистических данных в виде таблиц частот и относительных частот. Учащимся предлагаются задания на нахождение среднее арифметическое, мода, размах. Рассматривается вопрос о наглядной интерпретации статистической информации. Известные учащимся способы наглядного представления статистических данных с помощью столбчатых и круговых диаграмм расширяются за счет введения таких понятий, как полигон и гистограмма.
-
Повторение.
Содержание обучения курса геометрии.
-
Четырехугольники.
Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии.
Основная цель - изучить наиболее важные виды четырехугольников - параллелограмм, прямоугольник, ромб, квадрат, трапецию; дать представление о фигурах, обладающих осевой и центральной симметрией.
Доказательства большинства теорем данной темы и решение многих задач проводятся с помощью признаков равенства треугольников, поэтому полезно их повторить в начале изучения темы.
Осевая и центральные симметрии вводятся не как преобразование, а как свойства геометрических фигур, в частности четырехугольников. Рассмотрение этих понятий как движений плоскости состоится в 9 классе.
-
Площадь.
Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
Основная цель - расширить и углубить полученные в 5-6 классах представления учащихся об измерении и вычислении площадей; вывести формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; доказать одну из главных теорем геометрии - теорему Пифагора.
Вывод формул для вычисления площадей прямоугольника, параллелограмма, треугольника, трапеции основывается на двух основных свойствах площадей, которые принимаются исходя из наглядных представлений, а также на формуле площади квадрата, обоснование которой не является обязательным для учащихся.
Нетрадиционной для школьного курса является теорема об отношении площадей треугольника, имеющих по равному углу. Она позволяет в дальнейшем дать простое доказательство признакам подобия треугольников. В этом состоит одно из преимуществ, обусловленных ранним введением понятия площади.
Доказательство теоремы Пифагора основывается на свойствах площадей и формулах для площадей квадрата и прямоугольника. Доказывается также теорема, обратная теореме Пифагора.
-
Подобные треугольники.
Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.
Основная цель - ввести понятие подобных треугольников; рассмотреть признаки подобия треугольников и их применения; сделать первый шаг в освоении учащимися тригонометрического аппарата геометрии.
Определение подобных треугольников дается не на основе преобразования подобия, а через равенство углов и пропорциональность сходственных сторон.
Признаки подобия треугольников доказываются с помощью теоремы об отношении площадей треугольников, имеющих по равному углу.
На основе признаков подобия доказывается теорема о средней линии треугольника, утверждение о точке пересечения медиан треугольника, а также два утверждения о пропорциональных отрезках в прямоугольном треугольнике. Дается представление о методе подобия в задачах на построение.
В заключение темы вводятся элементы тригонометрии - синус, косинус и тангенс острого угла прямоугольного треугольника.
-
Окружность.
Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.
Основная цель - расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, связанные с окружностью; познакомить учащихся с четырьмя замечательными точками треугольника.
В данной теме вводится много новых понятий и рассматривается много утверждений, связанных с окружностью. Для их усвоения следует уделить большое внимание решению задач.
Утверждение о точке пересечения биссектрис треугольника и точке пересечения серединных перпендикуляров к сторонам треугольника выводятся как следствия из теорем о свойствах биссектрисы угла и серединного перпендикуляра к отрезку. Теорема о точке пересечения высот треугольника (или их продолжений) доказывается с помощью утверждения о точке пересечения серединных перпендикуляров.
Наряду с теоремами об окружностях, вписанных в треугольник и описанных около него, рассматриваются свойства сторон описанного четырехугольника и свойства углов вписанного четырехугольника.
-
Повторение. Решение задач.
Требования к уровню подготовки выпускников.
В результате изучения курса математики 8-го класса учащиеся должны знать/понимать
-
существо понятие математического доказательства; приводить примеры доказательств;
-
существо понятия алгоритма; приводить примеры алгоритмов;
-
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
-
как потребности практики привели математическую науку к необходимости расширения понятия числа;
-
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
-
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
-
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
В результате изучения курса математики 8-го класса учащиеся должны уметь:
-
выполнять устно арифметические действия: сложения и вычитание двухзначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
-
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты - в виде дроби и дробь - в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
-
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значение степеней с целыми показателями и корней; находить значение числовых выражений;
-
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
-
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
-
решать текстовые задачи, включая задачи связанные с отношением и с пропорциональностью величин, дробями и процентами;
-
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
-
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
-
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
-
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
-
решать линейные неравенства с одной переменной и их системы;
-
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
-
изображать числа точками на координатной прямой;
-
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
-
находить значение функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
-
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
-
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
-
вычислять средние значения результатов измерений;
-
находить частоту события, используя собственные наблюдения и готовые статистические данные;
-
пользоваться математическим языком для описания предметов окружающего мира;
-
распознавать геометрические фигуры, различать их взаимное расположение;
-
изображать геометрические фигуры: выполнять чертежи по условию задач; осуществлять изображение фигур;
-
вычислять значение геометрических величин (длин, углов, площадей, объемов); в том числе: для углов от 0 до 180 определять значения тригонометрических функций по заданным значениям углов; находить значение тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур, составленных из них;
-
решать геометрические задачи, опираясь на изученные свойства фигур и отношения между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
-
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
Применять полученные знания:
-
для решения несложных практических задач, в том числе с использованием, при необходимости, справочных материалов и простейших расчетных устройств;
-
для устной прикидки и оценки результата вычислений; проверки результата вычисления на правдоподобие, используя различные приемы; интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
-
для выполнения расчетов по формулам, понимая формулу как алгоритм вычисления; для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
-
при моделировании практических ситуаций и исследовании построенных моделей (используя аппарат алгебры);
-
при интерпретации графиков зависимостей между величинами; переводя на язык функций и исследуя реальные зависимости;
-
для расчетов, включающих простейшие тригонометрические формулы;
-
при построениях геометрическими инструментами (линейка, угольник, циркуль, транспортир);
-
для вычисления длин, площадей основных геометрических фигур с помощью формул (используя при необходимости справочники и технические средства).
Учебно-тематический план по алгебре
№
Содержание материала
Кол-во часов
1
Рациональные дроби
23
2
Квадратные корни
19
3
Квадратные уравнения
21
4
Неравенства
20
5
Степень с целым показателем. Элементы статистики.
11
6
Повторение
8
Всего
102
Учебно-тематический план по геометрии
№
Содержание материала
Кол-во часов
1
Четырехугольники
14
2
Площадь
14
3
Подобные треугольники
19
4
Окружность
17
5
Повторение. Решение задач.
4
Всего
68
Материально-техническое и учебно-методическое обеспечения
-
Алгебра. 8 класс: поурочные планы по учебнику Ю.Н. Макарычева и др. / авт.-сост. Т.Л. Афанасьева, Л.А. Тапилина. - Волгоград: Учитель, 2007. - 303 с.
-
Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Теляковского. М.: Просвещение, 2002.
-
Гаврилова Н.Ф. Поурочные разработки по геометрии 8 класс. М.»вако» 2011
-
Дидактические материалы по алгебре для 8 класса / В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк. - М.: Просвещение, 2006. - 144 с.
-
Гласков Ю.А., Гаиашвили М.Я. Тесты по алгебре 8 класс, - М.: «экзамен», 2011.
-
Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель: Бурмистрова Т.А. - М.: Просвещение, 2009 г.
-
Программы общеобразовательных учреждений. Геометрия. 7-9 классы. Составитель: Бурмистрова Т. А. - Москва «Просвещение» 2009 г.
-
Фарков А.В. тесты по геометрии к учебнику Л.С. Атанасян и др. «Геметрия 7-9» 8 класс. Издательство «Экзамен» 2011.
-
Интерактивная доска Smart 660 д.
-
Мультимедийный проектор Acer Х1130
-
Компьютер в сборе монитор Acer AL 1716
1). Интерактивное учебное пособие:
-тригонометрические функции, уравнения и неравенства; «Наглядная математика»:
-стереометрия; «Наглядная математика»:
-генератор заданий по математике, контрольные и самостоятельные работы; « Экзамен»
-математика 5-11 класс, Практикум; образовательный комплекс «Школа»
-геометрия 7-9 классы Издательство « Учитель»
-интерактивная математика 5-9 классы, Издательство «Дрофа»
- математика планиметрия 7-9 классы «Умник».
12.
Приложение
Календарно-тематическое планирование (всего 105 часа: 3 часа в неделю)
Алгебра 8 класс
№ урока
Содержание учебного материала
Кол-во часов
Время проведения
Глава I. Рациональные дроби
23
1-5
Рациональные дроби и их свойства
5
6-11
Сумма и разность дробей
6
12
Контрольная работа №1
1
13-22
Произведение частное дробей.
10
23
Контрольная работа №2
1
Глава II. Квадратные корни
19
24-25
Действительные числа
2
26-30
Арифметический квадратный корень
5
31-33
Свойства арифметического квадратного корня
3
34
Контрольная работа №3
1
35-41
Применение свойств арифметического квадратного корня.
7
42
Контрольная работа №4
1
Глава III. Квадратные уравнения
21
43-52
Квадратные уравнения и его корни
10
53
Контрольная работа №5
1
54-62
Дробно-рациональные уравнения.
9
63
Контрольная работа №6
1
Глава IV. Неравенства
20
64-71
Числовые неравенства и их свойства
8
72
Контрольная работа № 7
1
73-82
Неравенства с одной переменной и их системы
10
83
Контрольная работа № 8
1
Глава V. Степень с целым показателем. Элементы статистики.
11
84-89
Степень с целым показателем и ее свойства
6
90
Контрольная работа №9
1
91-94
Элементы статистики
4
Повторение
8
95-99
Повторение
5
100
Итоговый зачет
1
101-102
Итоговая контрольная работа
2
Лист корректировки рабочей программы
№ урока
Тема урока
Причины корректировки
Способ корректировки
Календарно-тематическое планирование (всего 68 часов: 2 часа в неделю)
Геометрия 8 класс
Глава V. Четырехугольники
14
1-2
Многоугольники
2
3-8
Параллелограмм и трапеция
6
9-12
Прямоугольник, ромб, квадрат
4
13
Решение задач
1
14
Контрольная работа №1
1
Глава VI. Площадь
14
15-16
Площадь многоугольника
2
17-22
Площадь параллелограмма, треугольника и трапеции
6
23-25
Теорема Пифагора
3
26-27
Решение задач
2
28
Контрольная работа №2
1
Глава VII. Подобные треугольники
19
29-30
Определение подобных треугольников.
2
31-35
Признаки подобия треугольников.
5
36
Контрольная работа №3
1
37-43
Применение подобия к доказательству теорем и решению задач.
7
44-46
Соотношения между сторонами и углами прямоугольного треугольника
3
47
Контрольная работа №4
1
Глава VIII. Окружность
17
48-50
Касательная к окружности.
3
51-54
Центральные и вписанные углы
4
55-57
Четыре замечательные точки треугольника.
3
58-61
Вписанная и описанная окружности
4
62-63
Решение задач
2
64
Контрольная работа. Окружность.
1
Повторение
4
65-68
Повторение
4
2
Лист корректировки рабочей программы
№ урока
Тема урока
Причины корректировки
Способ корректировки
Контрольные работы по алгебре
Контрольная работа №1
Вариант I
-
Сократите дробь:
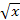
-
Представьте в виде дроби:
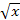
-
Найдите значение выражения
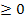 при
при 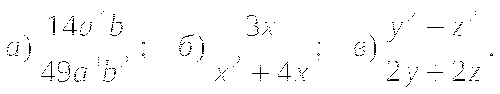
-
Упростить выражение:
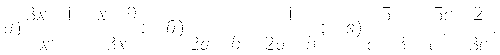
-
При каких целых значениях a является целым числом значение выражения
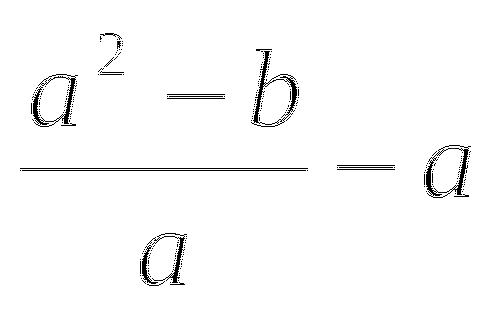 ?
?
Вариант II
-
Сократите дробь:
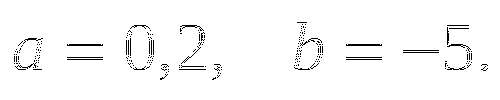
-
Представьте в виде дроби:
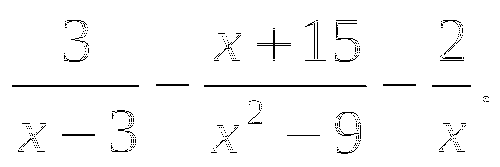
-
Найдите значение выражения
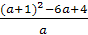 при
при 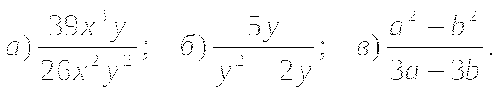
-
Упростить выражение:

-
При каких целых значениях b является целым числом значение выражения
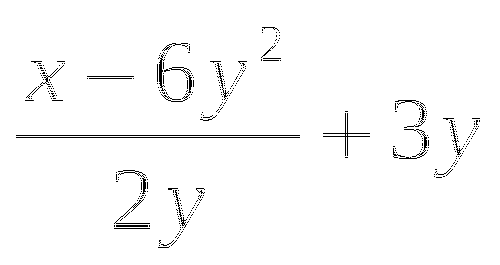 ?
?
Контрольная работа №2
Вариант I
-
Представьте выражение в виде дроби:
![]()
-
Постройте график функции
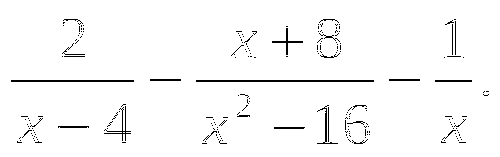 . Какова область определения функции? При каких значениях
. Какова область определения функции? При каких значениях 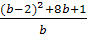 функция принимает отрицательные значения?
функция принимает отрицательные значения? -
Докажите, что при всех значениях
 значение выражения
значение выражения 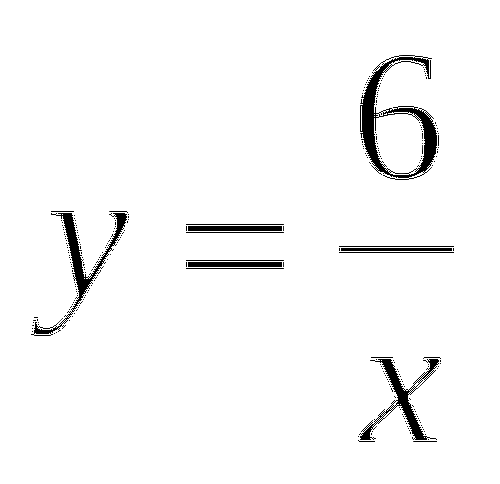 не зависит от
не зависит от  .
. -
При каких значениях a имеет смысл выражение
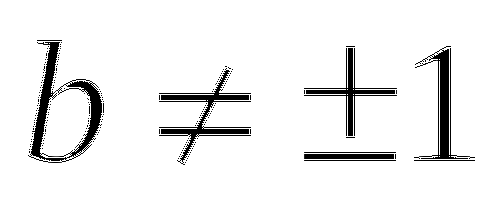
Вариант II
-
Представьте выражение в виде дроби:
![]()
-
Постройте график функции
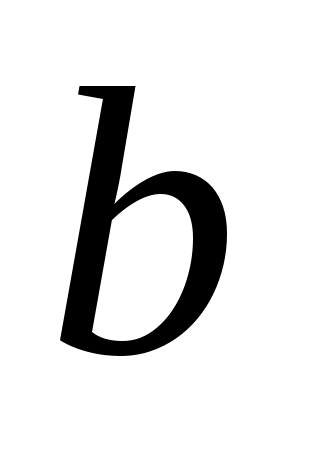 . Какова область определения функции? При каких значениях
. Какова область определения функции? При каких значениях 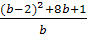 функция принимает отрицательные значения?
функция принимает отрицательные значения? -
Докажите, что при всех значениях
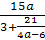 значение выражения
значение выражения  не зависит от
не зависит от 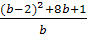 .
. -
При каких значениях b имеет смысл выражение
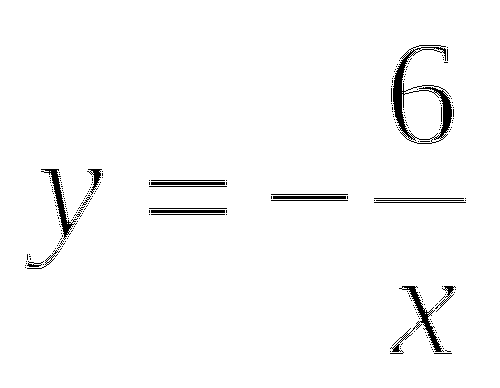
Контрольная работа №3
Вариант I
-
Вычислите: а)
 б)
б) 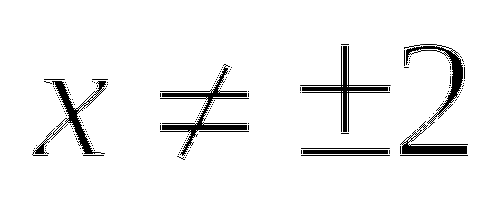 в)
в) 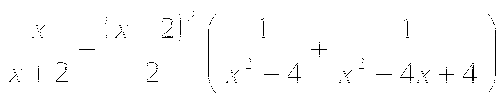
-
Найдите значение выражения:
а) ![]()
-
Решить уравнения: а)
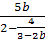
-
Упростить выражение: а)
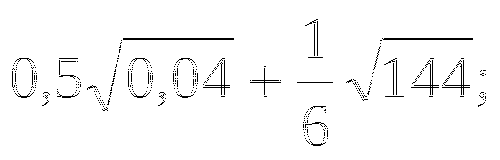
-
Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число
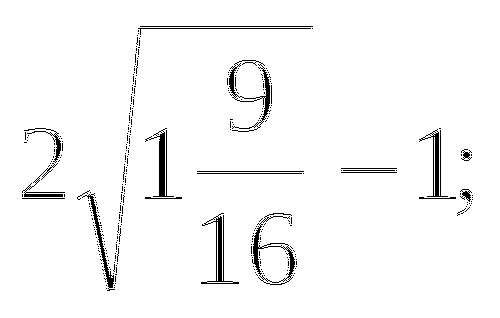
-
При каких значениях переменной a имеет смысл выражение
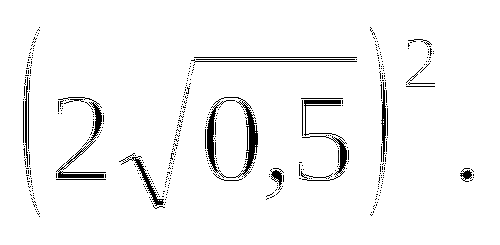
Вариант II
-
Вычислите: а)
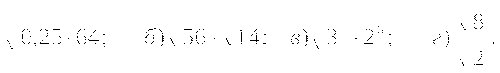 б)
б)  в)
в) 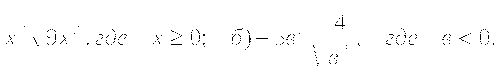
-
Найдите значение выражения:
а) ![]()
-
Решить уравнения: а)
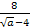
-
Упростить выражение: а)
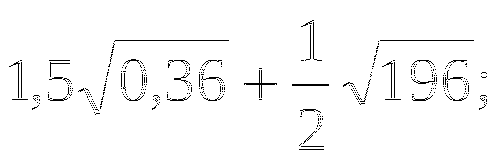
-
Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число
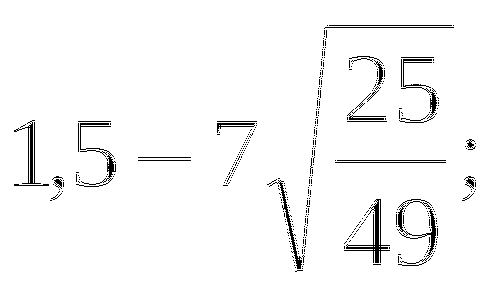
-
При каких значениях переменной x имеет смысл выражения
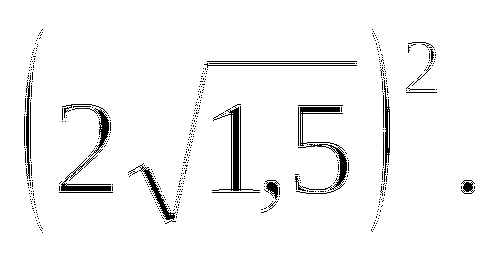
Контрольная работа №4
Вариант I
-
Упростите выражение:
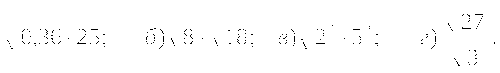
-
Сравните:
 и
и 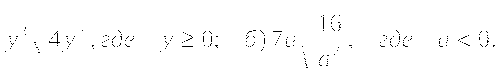 .
. -
Сократите дробь:
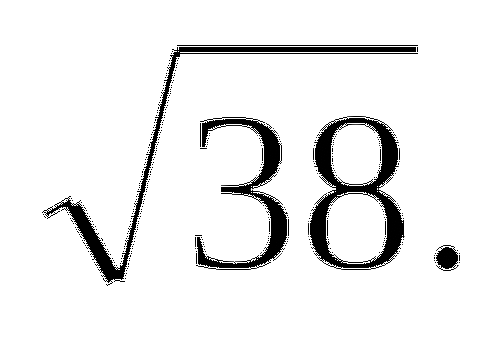
-
Освободите дробь от знака корня в знаменателе:
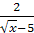
-
Докажите, что значение выражения
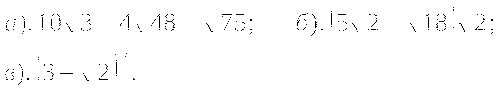 есть число рациональное.
есть число рациональное. -
При каких значениях a дробь
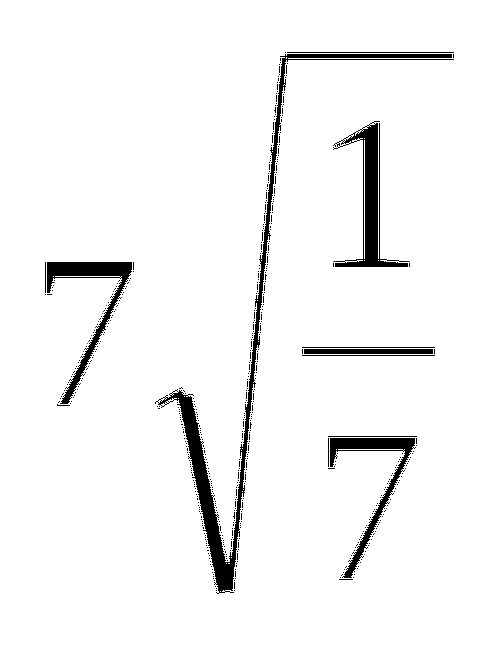 принимает наибольшее значение?
принимает наибольшее значение?
Вариант II
-
Упростите выражение:
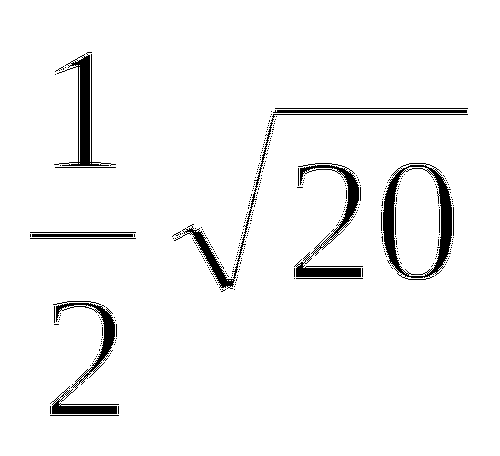
-
Сравните:
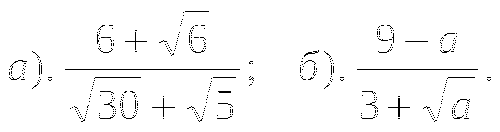 и
и 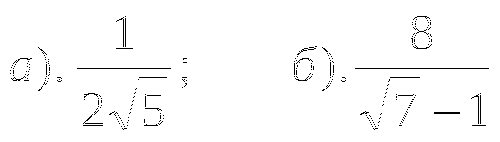 .
. -
Сократите дробь:
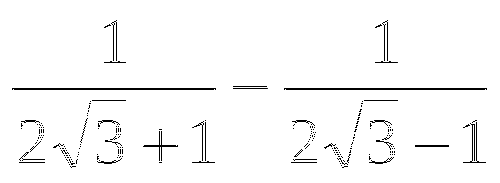
-
Освободите дробь от знака корня в знаменателе:
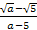
-
Докажите, что значение выражения
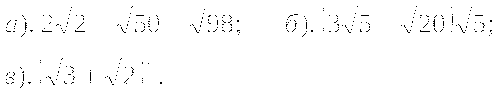 есть число рациональное.
есть число рациональное. -
При каких значениях x дробь
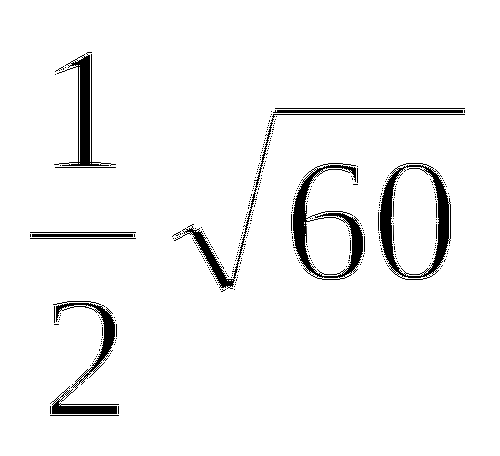 принимает наибольшее значение?
принимает наибольшее значение?
Контрольная работа №5
Вариант I
-
Решите уравнение: а) 2x2+7x-9=0; б) 3x2=18x; в) 100x2-16=0; г) x2-16x+63=0
-
Периметр прямоугольника 20 см. Найдите его стороны, если известно, что площадь прямоугольника 24см².
-
В уравнении
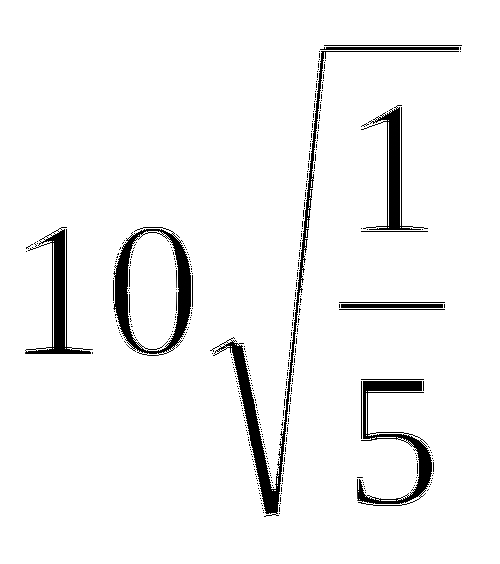 один из корней равен -9. Найдите другой корень и коэффициент p.
один из корней равен -9. Найдите другой корень и коэффициент p.
Вариант II
-
Решите уравнение: а) 3x2+13x-10=0; б) 2x2-3x=0; в) 16x2=49; г) x2-2x-35=0
-
Периметр прямоугольника 30 см. Найдите его стороны, если известно, что площадь прямоугольника 56см².
-
В уравнении x2+11x+q=0 один из корней равен -7. Найдите другой корень и коэффициент q.
Контрольная работа №6
Вариант I
-
Решить уравнение: а)
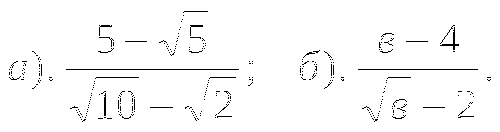 б)
б) 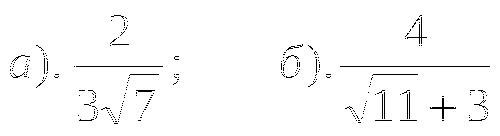
-
Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он все же на обратный путь затратил времени на 10 минут меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В?
Вариант II
-
Решить уравнение: а)
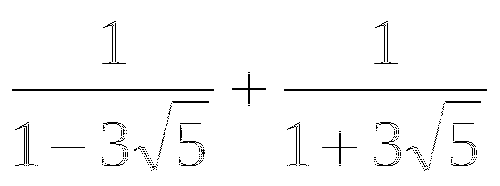 б)
б) 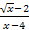
-
Катер прошел 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему понадобилось бы, если бы он шел 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч?
Контрольная работа №7
Вариант I
-
Докажите неравенство:
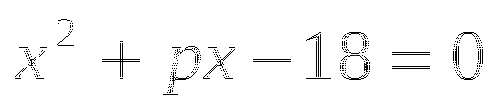
-
Известно, что
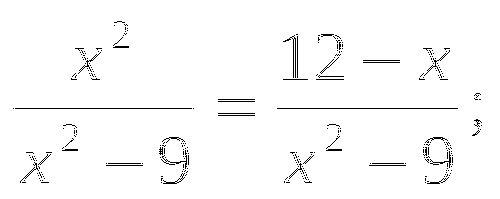 . Сравните:
. Сравните: 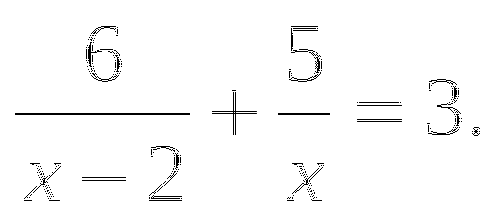
-
Известно, что
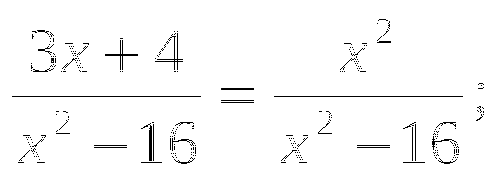 . Оцените:
. Оцените: 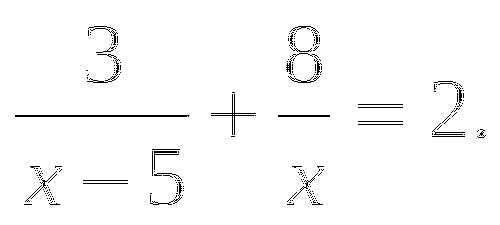
-
Оцените периметр и площадь прямоугольника со сторонами
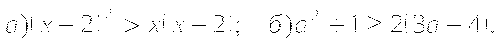 см и
см и  см, если известно, что
см, если известно, что 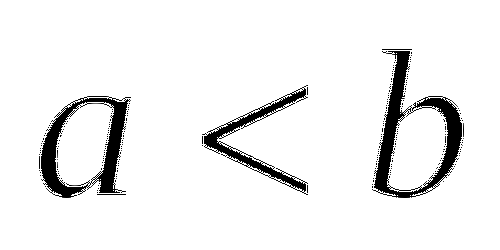
-
К каждому из чисел 2, 3, 4 и 5 прибавили одно и тоже число
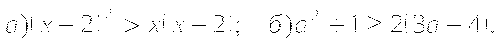 . Сравните произведение крайних членов получившейся последовательности с произведением средних членов.
. Сравните произведение крайних членов получившейся последовательности с произведением средних членов.
Вариант II
-
Докажите неравенство:

-
Известно, что
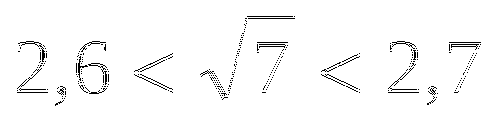 . Сравните:
. Сравните: 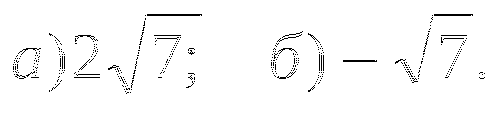
-
Известно, что
 . Оцените:
. Оцените: 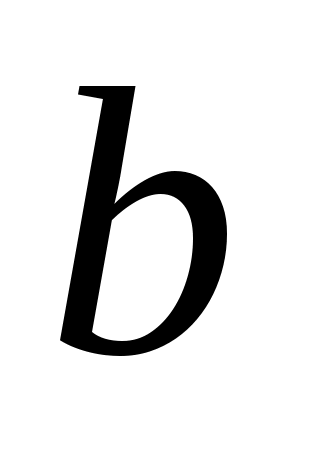
-
Оцените периметр и площадь прямоугольника со сторонами
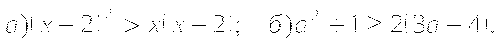 см и
см и  см, если известно, что
см, если известно, что 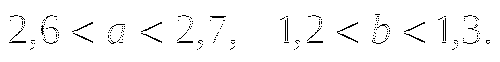
-
К каждому из чисел 6, 5, 4 и 3 прибавили одно и тоже число
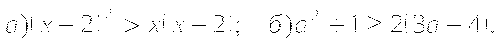 . Сравните произведение крайних членов получившейся последовательности с произведением средних членов.
. Сравните произведение крайних членов получившейся последовательности с произведением средних членов.
Контрольная работа №8
Вариант I
-
Решите неравенство: а)
 б) 1-3x≤0; в) 5(y-1,2)-4,6>3y+1
б) 1-3x≤0; в) 5(y-1,2)-4,6>3y+1 -
При каких a значение дроби
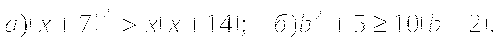 меньше соответствующего значения дроби
меньше соответствующего значения дроби 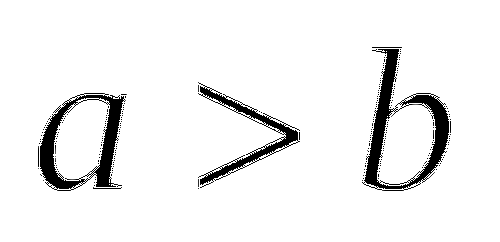
-
Решите систему неравенств:
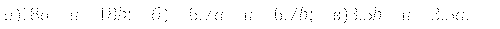
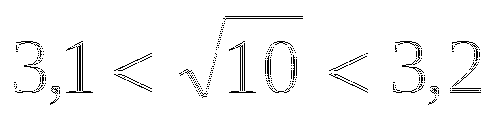
-
Найдите целые решения системы неравенств
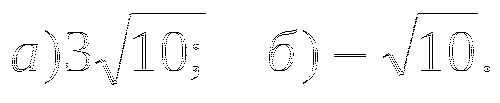
-
При каких значениях x имеет смысл выражение
 +
+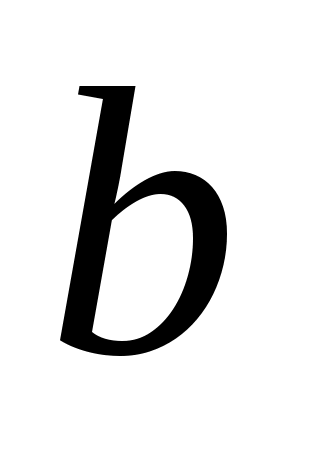
-
При каких значениях a множеством решений неравенства 3x-7<
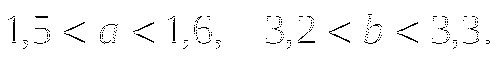 является числовой промежуток (-∞;4)?
является числовой промежуток (-∞;4)?
Вариант II
-
Решите неравенство: а)
 б) 2-7x>0; в) 6(y-1,5)-3,4>4y-2,4
б) 2-7x>0; в) 6(y-1,5)-3,4>4y-2,4 -
При каких a значение дроби
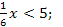 меньше соответствующего значения дроби
меньше соответствующего значения дроби 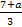
-
Решите систему неравенств:
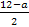
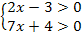
-
Найдите целые решения системы неравенств
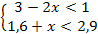
-
При каких значениях a имеет смысл выражение
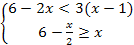 +
+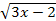
-
При каких значениях b множеством решений неравенства 4x+6>
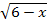 является числовой промежуток (3; +∞)?
является числовой промежуток (3; +∞)?
Контрольная работа №9
Вариант I
-
Найдите значение выражения: а) 411*4-9 б) 6-5:6-3 в) (2-2)3
-
Упростите выражение: а) (x-3)4*x14 б) 1,5a2b-3*4a-3b4.
-
Преобразуйте выражение: а) (
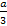 x-1y2)-2 б) (
x-1y2)-2 б) (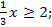 )-1*6xy2
)-1*6xy2 -
Вычислите:
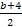
-
Представьте произведение (4,6*104)*(2,5*10-6) в стандартном виде числа.
-
Представьте выражение (a-1+b-1)(a+b)-1 в виде рациональной дроби.
Вариант II
-
Найдите значение выражения: а) 5-4*52; б) 12-3:12-4; в) (3-1)-3.
-
Упростите выражение: а) (a-5)4*a22; б) 0,4x6y-8*50x-5y9.
-
Преобразуйте выражение: а) (
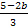 x-4y3)-1 б) (
x-4y3)-1 б) (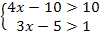 )-2*10a7b3
)-2*10a7b3 -
Вычислите:
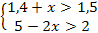
-
Представьте произведение (3,5*10-5)*(6,4*102) в стандартном виде числа.
-
Представьте выражение (x-1-y-1)(x-y)-1 в виде рациональной дроби.
Итоговая контрольная работа
Вариант I
-
Решите систему неравенств
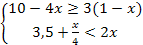
-
Упростите выражение (
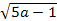 +
+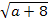 )
) -2
-2
-
Упростите выражение
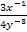
-
Два автомобиля выезжают одновременно из одного города в другой, находящийся на расстоянии 560 км. Скорость первого на 10 км/ч больше скорости второго, и поэтому первый автомобиль приезжает на место на 1 час раньше второго. Определите скорость каждого автомобиля.
-
При каких значениях x функция y= -
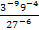 принимает положительное значение?
принимает положительное значение?
Вариант II
-
Решите систему неравенств

-
Упростите выражение
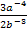
-
Упростите выражение
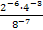 :
: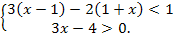
-
Пассажирский поезд был задержан в пути на 16 мин и нагнал опоздание на перегоне в 80 км, идя со скоростью на 10 км/ч большей, чем полагалась по расписанию. Какова была скорость поезда по расписанию?
-
При каких значениях x функция y=
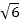 принимает отрицательное значение?
принимает отрицательное значение?
Контрольные работы по геометрии
Контрольная работа №1
Вариант I
-
Диагонали прямоугольника ABCD пересекаются в точке O. Найдите угол между диагоналями, если угол AOB=300.
-
В параллелограмме KMNP проведена биссектриса угла MKP, которая пересекает сторону MN в точке E.
а) Докажите, то треугольник KME равнобедренный.
б) Найдите сторону KP, если ME=10 см, а периметр параллелограмма равен 52 см.
Вариант II
-
Диагонали ромба KMNP пересекаются в точке O. Найдите углы треугольника KOM, если угол MNP=800.
-
На стороне BC параллелограмма ABCD взята точка M так, что AB=BM.
а) Докажите, что AM - биссектриса угла BAD.
б) Найдите периметр параллелограмма, если CD=8 см, CM=4 см.
Контрольная работа №2
Вариант I
-
Смежные стороны параллелограмма равны 32 см и 26 см, а один из его углов равен 1500. Найдите площадь параллелограмма.
-
Площадь прямоугольной трапеции равна 120 см2, а ее высота равна т8 см. найдите все стороны трапеции, если одно из оснований больше другого на 6 см.
-
На стороне AC данного треугольника ABC постройте точку D так, чтобы площадь треугольника ABD составила одну треть площади треугольника ABC.
Вариант II
-
Одна из диагоналей параллелограмма является его высотой и равна 9 см. найдите стороны этого параллелограмма, если его площадь равна 108 см2.
-
Найдите площадь трапеции ABCD с основанием AD и BC, если известно, что AB=12 см, BC=14 см, AD=30 см, угол B=1500.
-
На продолжении стороны KN данного треугольника KMN постройте точку P так, чтобы площадь треугольника NMP была в два раза меньше площади треугольника KMN.
К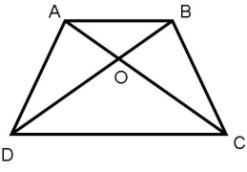 онтрольная работа №3
онтрольная работа №3
Вариант I
-
На рисунке АВ || CD.
а) Докажите, что АО : ОС = ВО : OD.
б) Найдите АВ, если OD = 15 см, ОВ = 9 см, CD = 25 см.
-
Найдите отношение площадей треугольников ABC и KMN, если АВ = 8 см, ВС = 12 см, АС = 16 см, КМ = 10 см, MN = 15 см, NK = 20 см.
В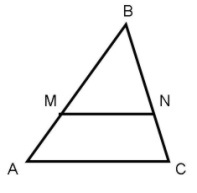 ариант II
ариант II
-
На рисунке MN || АС.
а) Докажите, что AB*BN=CB*BM.
б) Найдите MN, если AM = 6 см, ВМ = 8 см, АС = 21 см.
-
Даны стороны треугольников PQR и ABC: PQ = 16 см, QR = 20 см, РR = 28 см и АВ= 12 см, ВС = 15 см, АС = 21 см. Найдите отношение площадей этих треугольников.
Контрольная работа №4
Вариант I
-
В прямоугольном треугольнике ABC угол A=900, AB=20 см, высота AD=12 см. найдите AC и cos C.
-
Диагональ BD параллелограмма ABCD перпендикулярна к стороне AD. Найдите площадь параллелограмма ABCD, если AB=12 см, угол A=410
Вариант II
-
Высота BD прямоугольного треугольника ABC равна 24 см и отсекает от гипотенузы AC отрезок DC, равный 18 см. Найдите ABи cos A.
-
Диагональ AC прямоугольника ABCD равна 3 см и составляет со стороной AD угол 370. Найдите площадь прямоугольника ABCD.
Контрольная работа №5
Вариант I
-
Через точку A окружности проведены диаметр AC и две хорды AB и AD, равные радиусу окружности. Найдите углы четырехугольника ABCD и градусные меры дуг AB, BC, CD, AD.
-
Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Вариант II
-
Отрезок BD - диаметр окружности с центром O. хорда AC делит пополам радиус OB и перпендикулярна к нему. Найдите углы четырехугольника ABCD и градусные меры дуг AB, BC, CD, AB.
-
Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.