Проект по математике в 5 классе История возникновения обыкновенных дробей

Муниципальное бюджетное общеобразовательное учреждение

«Гимназия №6 им. академика - кораблестроителя А.Н. Крылова»

г. Алатырь Чувашской Республики

Проект

«История возникновения обыкновенных дробей»

Выполнил:

ученик 5в класса

Чунин Михаил.

Руководитель:

Трушина Н.В.

Алатырь 2016

ОГЛАВЛЕНИЕ

Введение …………………………………………………………………...3

§1. История возникновения обыкновенных дробей…………………….4

§2. Старинные задачи на дроби и их решение…………………………...7

Заключение…………………………………………………………………8

Приложения………………………………………………………………...9

Список используемой литературы………………………………………11

2

Введение.

Необходимость в дробных числах возникла у человека на весьма ранней стадии развития. Уже дележ добычи, состоявший из нескольких убитых животных, между участниками охоты, когда число животных оказывалось не кратным числу охотников, могло привести первобытного человека к понятию о дробном числе.

Наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удаётся выразить натуральным числом, приходится учитывать и части употребляемой меры. Исторически дроби возникли в процессе измерения.

На уроках математики при изучении темы «Обыкновенные дроби» я узнал некоторые исторические факты из появления и развития дробей. К сожалению, этому вопросу мы не смогли уделить достаточного внимания на уроке, а меня этот вопрос заинтересовал и захотелось рассмотреть его более основательно: рассмотреть более подробно этапы развития обыкновенных дробей; найти задачи с дробями, составленные в далёком прошлом.

Объект исследования: обыкновенные дроби.

Предмет исследования: история возникновения обыкновенных дробей.

Исходя из выше сказанного, я поставил следующие задачи и цель.

Цель исследования: изучить вопрос об истории возникновения обыкновенных дробей.

Задачи исследования:

1. Обобщить исторический материал: когда и где впервые упоминается о дробях.

2. Составить перечень способов записи дроби в разные эпохи и у разных народов; перечень старинных задач на дроби.

3

§1. История возникновения обыкновенных дробей.

Необходимость в дробных числах возникла у человека на весьма ранней стадии развития. Уже дележ добычи, состоявший из нескольких убитых животных, между участниками охоты, когда число животных оказывалось не кратным числу охотников, могло привести первобытного человека к понятию о дробном числе.

Наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удаётся выразить натуральным числом, приходится учитывать и части употребляемой меры. Исторически дроби возникли в процессе измерения.

Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3 и более частей. Более мелкой единице меры, которую получали как следствие раздробления, давали индивидуальное название, и величины измеряли уже этой более мелкой единицей.

В связи с этой необходимой работой люди стали употреблять выражения: половина, треть, два с половиной шага. Откуда можно было сделать вывод, что дробные числа возникли как результат измерения величин. Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.

Дроби в Древнем Египте

В Древнем Египте архитектура достигла высокого развития. Для того, чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику.

Египтяне ставили иероглиф (ер, «[один] из» или ре, рот) над числом для обозначения единичной дроби в обычной записи, а в священных текстах использовали линию. К примеру:

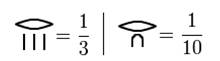
У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби (большие чем 1/2).

Остальные дроби они записывали в виде суммы долей. Дробь они записывали в виде ,но знак «+» не указывали. А сумму записывали в виде . Следовательно, такая запись смешанных чисел (без знака «+») сохранилась с тех пор.

Древние египтяне уже знали, как поделить 2 предмета на троих, для этого числа - 2/3 - у них был специальный значок. Это была единственная дробь в обиходе египетских писцов, у которой в числителе не стояла единица - все остальные дроби непременно имели в числителе единицу (так называемые основные дроби). Умели египтяне также умножать и делить дроби. Но для умножения приходилось умножать доли на доли, а потом, быть может, снова использовать таблицу. Ещё сложнее обстояло с делением. Важную работу по исследованию египетских дробей провёл математик XIII века Фибоначчи.

Изображение дробей в Древнем Египте представлено в приложении №1.

Дроби в Древней Греции

Поскольку греки работали с обыкновенными дробями лишь эпизодически, они использовали различные обозначения. Герон и Диофант, самые известные арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем числитель располагали под знаменателем.

4

Например, означало три пятых. Еще за 2-3 столетия до Евклида и Архимеда греки свободно владели арифметическими действиями с дробями.

Изображение дробей в Древней Греции представлено в приложении №2.

Дроби у арабов.

Записывать дроби как сейчас стали арабы. Средневековые арабы пользовались системами записи дробей, на индийский манер записывая знаменатель под числителем; дробная черта появилась в конце XII - начале XIII в. Применялись дроби со знаменателями, не превышающими 10 (только для таких дробей арабский язык имеет специальные термины); часто использовались приближенные значения; арабские ученые работали над усовершенствованием этого исчисления. Арабские ученые, как и греки, применяли алфавитную запись, распространив ее и на целые части.

Изображение дробей у арабов представлено в приложении №3.

Дроби в Вавилоне

Вавилоняне пользовались всего двумя цифрами. Вертикальная черточка обозначала одну единицу, а угол из двух лежащих черточек - десять. Эти черточки у них получались в виде клиньев, потому что вавилоняне писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали.

В древнем Вавилоне предпочитали постоянный знаменатель, равный 60-ти. Шестидесятеричными дробями, унаследованными от Вавилона, пользовались греческие и арабские математики и астрономы. Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы счисления. Скорее всего здесь учитывалось основание 60, которое кратно 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты.

Вавилонская математика оказала влияние на греческую математику. Следы вавилонской шестидесятеричной системы счисления удержались в современной науке при измерении времени и углов. До наших дней сохранилось деление часа на 60 мин., минуты на 60 с, окружности на 360 градусов, градуса на 60 мин., минуты на 60с.

Вавилоняне внесли ценный вклад в развитие астрономии. Шестидесятеричными дробями пользовались в астрономии ученые всех народов до XVII века, называя их астрономическими дробями. В отличие от них, дроби общего вида, которыми пользуемся мы, были названы обыкновенными.

Изображение дробей в Древнем Вавилоне - Приложение

Дроби на Руси

В русском языке слово "дробь" появилось лишь в VIII веке. Происходит слово "дробь" от слова "дробить, разбивать, ломать на части". У других народов название дроби также связано с глаголами "ломать", "разбивать", "раздроблять".

В русских рукописных арифметиках XVII века дроби называли долями, позднее «ломаными числами». В старых руководствах находили следующие названия дробей на Руси:

- половина, полтина, - треть,

- четь, - полтреть,

- полчеть, - полполтреть,

- полполчеть, - полполполтреть (малая треть),

5

- полполполчеть (малая четь), - пятина,

- седьмина, - десятина.

Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная позиционная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I.

Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало - зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.

6

§2. Старинные задачи на дроби и их решение.

В различных книжных пособиях я нашёл интересные задачи, которые были использованы в различные исторические периоды.

1) Известный физик А. В. Цингер в своих воспоминаниях о Л. Н. Толстом рассказывает о следующей задаче, которая очень нравилась известному писателю:

«Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру ещё остался участок, скошенный на другой день косцом за один день работы. Сколько косцов было в артели?»

Решение: если большой луг полдня косила вся артель и полдня пол - артели, то ясно, что за полдня пол-артели скашивает луга. Следовательно, на малом лугу остался нескошенным участок в . Если один косец скашивает в день луга, а скошено

было , то косцов было восемь.

В начале XVIII века в России было немного образованных людей. Одним из авторитетных</<font color="#000000"> учёных был Леонтий Филиппович Магницкий (), который в 1703 году издал первый печатный учебник по математике «Арифметика». По этому учебнику обучались многие поколения русских людей. В книге Магницкого много задач с разным содержанием, включая и дроби.

2) «Един человек выпьет кадь пития в 14 дней, а со женою выпьет тое же кадь в 10 дней. И ведательно есть, в колико дней жена его выпьет тое же кадь»

Решение: муж за день будет выпивать часть кади, а вместе с женой - часть, значит, жена за один день выпьет часть кади, а всё содержимое выпьет за 35 дней.

3) «Воз сена».

Лошадь съедает воз сена за месяц, коза - за два месяца, овца - за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?

Решение: Поскольку лошадь съедает воз сена за месяц, то за год (12 месяцев) она съест 12 возов сена. Так как коза съедает воз сена за 2 месяца, то за год она съест 6 возов. Овца съедает воз сена за три месяца, значит, за год она съест 4 воза. Вместе за год они съедят 12+6+4=22 воза сена. Тогда один воз сена они вместе съедят за 12:22= месяца.

7

Заключение.

Цель исследования достигнута: рассмотрен вопрос об истории возникновения обыкновенных дробей, а также собраны и решены некоторые старинные задачи на применение дробей.

Особый интерес в ходе проекта я испытал при решении старинных задач с использованием дробей. Считаю, что материал этой работы будет интересным для других учащихся. Он может быть использован как на уроке, так и для проведения внеклассных мероприятий по математике.

8

Приложение

Изображение дробей в Древнем Египте.

Приложение

Изображение дробей в Древней Греции

9

Приложение

Изображение дробей у арабов.

.

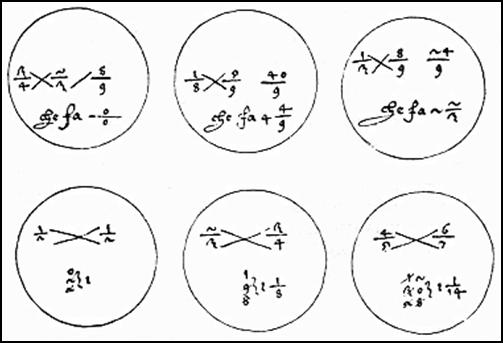
Приложение

Вавилонские таблички

10

Список используемой литературы

1. М. Я. Выгодский «Арифметика и алгебра в Древнем мире».

2. Г. И. Глейзер "История математики в школе"(М. Просвещение,1964г)

3. Г. И. Глейзер «История математики в школе».

4. И. Я. Депман «История арифметики».

5. А. Н. Колмогоров. Математика в её историческом развитии. - М.: Наука. Главная редакция физико-математической литературы, 199с.

6. С. Н. Олехник, Ю. В. Нестеренко, М. К. Потапов. Старинные занимательные задачи.- М.: Наука. Главная редакция физико-математической литературы, 1985. - 160 с.

7. Д. Я. Стройк. Краткий очерк истории математики. - М.: Наука. Главная редакция физико-математической литературы, 198с.

8. www. *****

9. *****/chisla/istoriya-poyavleniya-matematicheskoj-drobi/

11