Урок алгебры в 8 классе «Решение линейных неравенств»

Урок алгебры в 8 классе

«Решение линейных неравенств»

Цели урока:

Развитие личности учащихся на основе усвоения предметных знаний УУД.

-- отработать алгоритм решения линейных неравенств;

- выработать навыки применения данного алгоритма к ;

- развивать вычислительные навыки;

- развивать навыки самостоятельной работы.;

- развивать математическую речь.

Задачи урока: формирование УУД

Цели УУД:

Формирование коммуникативных УУД - учить высказывать суждения с использованием математических терминов и понятий таких, как числовые неравенства, свойства числовых неравенства, числовые промежутки; сотрудничать с товарищами при выполнении заданий в паре; сравнивать полученные результаты, выслушивать партнера, корректно сообщать товарищу об ошибках, задавать вопросы с целью получения нужной информации; организовывать взаимопроверку выполненной работы; высказывать свое мнение при обсуждении задания.

Формирование познавательных УУД - предлагать мыслительные операции в ходе поиска решения неравенства, применять правила - определение решения неравенства, перенос слагаемых, приведение подобных слагаемых, свойства неравенств, изображение решений неравенств на координатной прямой, запись ответа.

Формирование регулятивных действий:

- научить ученика контролировать, выполнять свои действия по заданному алгоритму, научить контролировать свою речь, помочь адекватно оценивать выполненную работу, проверять результаты вычислений, адекватно воспринимать указания на ошибки и исправлять найденные ошибки, оценивать собственные успехи в вычислительной деятельности.

Воспитательные задачи:

1. Воспитать целеустремленность, организованность, ответственность, самостоятельность.

2. Побуждать учащихся к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.

3. Развивать навыки коллективной работы, взаимопомощи.

4. Совершенствовать коммуникативные навыки.

5. Развивать навыки коллективной работы, взаимопомощи.

Тип урока:

Урок закрепления полученных знаний.

Предполагаемые результаты:

Повышение активности и самостоятельности на уроке.

Формы организации урока:

Индивидуальная, фронтальная, парная.

Оборудование:

1. Компьютерная презентация.

2. Учебники.

3. Карточки с заданиями с.р..

4. Экран.

План урока

1. Организационный момент.

2. Сообщение темы и целей урока.

3. Устная работа. Проверка домашнего задания.

4. Решение линейных неравенств.

5. Решение задачи с практическим содержанием

6. Подведение итогов урока.

7. Задание на дом.

Тип урока: Урок закрепления нового материала.

Вид урока: Комбинированный.

Ход урока.

1. Организационный момент.

Сообщение темы, целей урока и его девиза.

2. Мотивация урока.

Учитель начинает урок с того, что просит задуматься над тем, что в Кембриджском университете студентам часто напоминают следующее: «Если вы захотите поспать, то вам приснится ваша мечта. Если же вы окунетесь в учебу, то ваша мечта воплотится в жизнь». Давайте «окунемся в учебу, чтобы мечта воплотилась в жизнь».

Есть еще хорошие слова: Ян Амос Коменский сказал: «Считай несчастным тот день или тот час, в котором ты не усвоил ничего, ничего не прибавил к своему образованию».

И я надеюсь, что сегодняшний урок, и день не будет для вас несчастным и потерянным, т.к. каждый из вас унесёт с собой что-то новое, неизвестное, познавательное.

Актуализация опорных знаний.

Учитель: Ребята, мы сегодня продолжим решать линейные неравенства. Девизом сегодняшнего урока я выбрала высказывание великого математика Декарта: Математика учит преодолевать трудности и исправлять собственные ошибки. (Декарт).

Какие задачи перед собой поставим? (научиться решать неравенства, отработать алгоритм решения неравенств, применяя свойства неравенств).

Теоретический опрос:

Какие неравенства называются линейными неравенствами с одной переменной? (Неравенства вида ах<���������������������������������������������

���������

������������������������������������й переменной? (Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.)

Что значит "решить неравенство"? (Решить неравенство - значит найти все его решения или доказать, что таковых нет.)

Какие неравенства называются равносильными? (Неравенства, имеющие одни и те же корни называются равносильными. Неравенства, не имеющие решений, так же считаются равносильными.)

Какие свойства используются при решении неравенств?

1. Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство.

2. Если обе части неравенства разделить или умножить на одно и то же положительное число, то получится равносильное ему неравенство.

3. Если обе части неравенства разделить или умножить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.)

Что вы знаете о строгих, не строгих неравенствах? (слайд)

1. Какие свойства используются при решении неравенств? (слайд)

Устно:

Сейчас вам предстоит, используя свойства неравенств, решить следующие неравенства (работа в тетрадях и у доски), но знайте «Что математику нельзя изучить, наблюдая, как это делает сосед».

Давайте вспомним алгоритм решения неравенств первой степени с одной переменной:

1. Раскрыть скобки и привести подобные слагаемые.

2. Сгруппировать слагаемые с переменной в левой части неравенства, а без переменной - в правой части, при переносе меняя знаки.

3. Привести подобные слагаемые.

4. Разделить обе части неравенства на коэффициент при переменной, если он не равен нулю. При этом важно помнить, что знак неравенства сохраняется, если делить на положительное число, и знак неравенства меняется на противоположный, если делить на отрицательное число.

5. Изобразить множество решений неравенства на координатной прямой.

6. Записать ответ в виде числового промежутка.

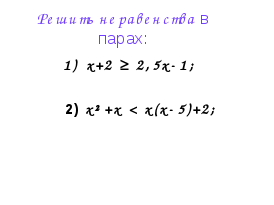
Работа с учебником.

№33.29(а,б) (2 человека у доски), №33.30(а,б)

Практическое применение линейных неравенств в решении задач.

Групповая работа (задачи практического содержания)

Учащиеся показывают выполнение домашнего задания. Класс разбился на группы, и каждая группа подготовила задачи на составление линейных неравенств с презентацией.

«Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их».

Д. Пойа.

Задача №1 . Расстояние между городами Липецк и Тамбов менее 210 км. Из города Липецк выехал грузовик со скоростью 60 км/ч, а из города Тамбов ему навстречу выехал автобус. Оцените, с какой скоростью должен ехать автобус, чтобы они могли встретиться через 2 часа?

2(х +60) < 210; ответ: х < 45км/ч.

«В задачах, которые ставит

перед нами жизнь,

экзаменатором является природа».

У. Сойер.

Задача №2. «Выбор транспорта»

Если первый автомобиль сделает 4 рейса и второй 4 рейса, то они перевезут меньше 21 т груза. Если первый автомобиль сделает 7 рейсов, а второй 1 рейс, то они перевезут больше 21 т груза. Какой автомобиль имеет большую грузоподъемность?

Решение:

Обозначим грузоподъемность первого автомобиля х, а второго у. Исходя из условия задачи, составим неравенства: 4х + 4у < 21 и 7х + у > 21. Опираясь на свойство числового неравенства: если а < в и в < с, то а < с, мы можем составить неравенство: 4х + 4у < 7х + у. Отсюда мы имеем:

3у < 3х, следовательно, у < х.

Ответ: грузоподъемность первого автомобиля больше.

Задача №3. Сколько железнодорожных платформ потребуется для перевозки 183 контейнеров, если на одной платформе можно разместить не более 5 контейнеров.

Задача №4. Турист проплыл на лодке некоторое расстояние по течению реки, а потом вернулся обратно, потратив на все путешествие не более пяти часов. Скорость лодки в стоячей воде равна 5 км/ч, а скорость течения - 1 км/ч. Какое наибольшее расстояние мог проплыть турист по течению реки?

Задача№5. В саду растут яблони, вишни и сливы, количества которых относятся как 5 : 4 : 2 соответственно. Каким может быть наименьшее количество вишен, если всего деревьев в саду не менее 120?

1) 11 2) 22 3) 44 4) 55

Задача №6. Если бы велосипедист проезжал в день на 10 км больше, чем на самом деле, то за 6 дней он проехал бы меньше 420 км. Если бы он проезжал в день 5 км меньше, чем на самом деле, то за 12 дней он проехал бы больше 420 км. Сколько километров мог проезжать за один день этот велосипедист?

Не далек тот день, когда нам с вами придется сдавать экзамен, предлагаю тестовые задания, которые встречаются на ОГЭ.

На выполнение теста 5 мин.

Проверяем. Оцените работу.

Самостоятельная работа (у каждого на столе лежит тест)

Задание на дом:

Рефлексия.

И прежде чем закончить урок, мне хочется рассказать вам притчу: «Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства храма. Мудрец остановил первого и спросил: «Что ты делал целый день?» Человек ответил, что возил проклятые камни. Второй ответил: « Я добросовестно выполнил свою работу ». А третий улыбнулся и сказал с радостью « Я принимал участие в строительстве храма! »

Давайте оценим каждый свою работу на уроке!

Кто работал как первый человек?

Кто работал добросовестно?

Кто принимал участие в строительстве храма?

Итоги: Выставьте себе баллы:
5 б-все понял и могу объяснить другому;
4 б-сам понял, но объяснить не берусь;
3 б-для полного понимания надо повторить;
2 б-я ничего не понял;