- Учителю
- Урок на тему: 'Комплексные числа и их геометрическая интерпретация'
Урок на тему: 'Комплексные числа и их геометрическая интерпретация'
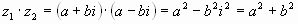
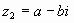
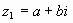
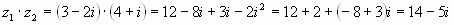
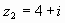
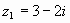
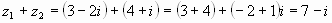
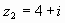
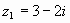
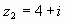
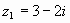
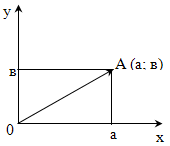
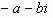
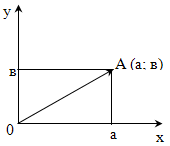
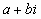
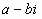
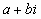
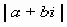
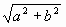
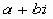
 Урок - лекция по теме
Урок - лекция по теме
«Комплексные числа и их геометрическая интерпретация»
Цель урока: познакомить учащихся с понятием комплексного числа; рассмотреть основные действия над комплексными числами.
Задачи урока.
Образовательные:
-
Ввести понятие комплексного числа и равных комплексных чисел .
-
Ввести понятие модуля комплексного числа
-
Рассмотреть геометрическую интерпретацию комплексных чисел.
-
Повторить историю развития чисел;
-
Показать необходимость расширения множеств натуральных, рациональных, действительных чисел;
-
Научить выполнять действия над комплексными числами;
Развивающие:
-
Развивать мышление в процессе выполнения практических заданий.
-
Развивать пространственные представления.
Воспитывающие:
-
Воспитывать культуру записей в тетради.
-
Воспитывать аккуратность, усидчивость, внимательность в процессе прослушивания лекции.
Тип урока: обзорная лекция.
План урока.
-
Организационный момент.
-
Изложение материала.
-
Домашнее задание.
-
Подведение итогов урока.
Ход урока
I. Организационный момент.
II. Изложение материала.
1. Вводная часть. Сегодня мы поговорим о числах, изучаемых в курсе математики. С какими числами вы уже знакомы? (Ответы учащихся). Зачем человеку нужно было придумывать различные множества чисел? (Потому что во множестве натуральных чисел не всегда можно выполнить вычитание и деление, во множестве рациональных чисел нельзя извлечь корень квадратный из положительного числа). Как геометрически можно изобразить натуральные, целые, рациональные, действительные числа?
2. История развития числа.
На первых этапах существования человеческого общества числа служили для примитивного счета предметов, дней, шагов. В первобытном обществе человек нуждался лишь в нескольких первых числа. С развитием цивилизации ему потребовалось изобретать все больше числа, этот процесс продолжался на протяженности многих столетий и требовал напряженного интеллектуального труда. При обмене продуктами появилась необходимость сравнивать числа, возникли понятия больше, меньше, равно. На этом же этапе люди стали складывать числа, затем научились вычитать, делить, умножать. При делении двух натуральных чисел появились дроби, при вычитании - отрицательные числа.
Так, например, во множестве натуральных чисел не всегда можно выполнить действия вычитания и деления. Расширив это множество до множества целых чисел , получаем возможность выполнить вычитание. Дальнейшее расширение до множества рациональных чисел позволяет кроме вычитания осуществлять и деление (исключая деление на нуль). И, наконец, построение более обширного множества действительных чисел дает возможность получить приближенное значение корня и т.д.
Необходимость выполнять арифметические действия привела к понятию рациональных чисел. В IV в. до н.э. греческие математики открыли несоизмеримые отрезки, длины которых не выражались ни целым, ни дробным числом (например, длина диагонали квадрата со стороной, равной 1). Потребовалась не одна сотня лет, чтобы математики смогли выработать способ записи таких чисел в виде бесконечной непериодической десятичной дроби. Так появились иррациональные числа, которые вместе с рациональными назвали действительными числами.
Но затем выяснилось, что во множестве действительных чисел не имеют решения простейшие квадратные уравнения, например, х2 + 1 = 0. Математики пришли к необходимости расширить понятия числа, чтобы в новом множестве можно было всегда извлечь квадратный корень. Новое множество назвали множеством комплексных чисел, введя понятие мнимой единицы: i2 = - 1.
Выражение вида а + вi назвали комплексным числом. Долгое время многие ученые не признавали их за числа. Только после того, как нашли возможность представить мнимое число геометрически, так называемые мнимые числа получили свое место во множестве чисел.
2. Введение понятия комплексного числа.
Запишем в тетрадях историю развития числа на языке множеств, используя круги Эйлера. В тетрадях должен появиться чертеж. N - натуральные числа. Q - рациональные числа. R - действительные числа.
Попробуйте сформулировать тему нашего урока (Выслушиваются предложения учащихся). Итак, тема занятия «Комплексные числа». Скажите, зачем нужно было расширять множества натуральных, целых, рациональных, действительных чисел? (Чтобы можно было выполнять любые действия над числами).
Определение. Комплексными называются числа вида а + вi, где а и в - действительные числа, i - мнимая единица: i2 = - 1. а называется действительной частью, вi - мнимой частью комплексного числа. [1]
Придумайте и запишите в тетрадях три комплексных числа.
Определение. Два комплексных числа называются равными, если равны их действительные части и коэффициенты при мнимых частях,
т.е. а + вi = с + di a = c, b = d.
Для комплексных чисел не существует соотношений «больше», «меньше».
Модулем комплексного числа называется неотрицательное число, равное и обозначается .
Два комплексных числа и называются сопряженными. Комплексные числа вида и называются противоположными.
Примеры: Найдите действительные числа х и у из уравнение числа, воспользовавшись тем, что если комлексные числа равны, то их мнимая и действительная часть соответственно равны.
Два студента выходят к доске.
а) х - 8i + (у - 3)i = 1 б) (3 + i) х - 2 (1 + 4i) у = - 2 - 4i
4. Действия над комплексными числами.
Определение. Суммой двух комплексных чисел а + вi = с + di называется комплексное число, равное (а + с) + (в +d) i.
Определение. Числа а + вi и - а - вi называются противоположными.
Действительно, (а + вi) + (- а - вi) = (а - а) + (в - в)i = 0 + 0i = 0.
Определение. Числа а + вi и а - вi называются сопряженными. Два комплексных числа z = a + bi и 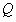 = a - bi, отличающиеся лишь знаком мнимой части, называются сопряженными.
= a - bi, отличающиеся лишь знаком мнимой части, называются сопряженными.
(а + вi) + (а - вi) = 2а;
(а + вi) + (а - вi) = a2 - (bi)2 = a2 - b2i2 = a2 - b2 (- 1) = a2 + b2.
Найдем произведение двух комплексных чисел:
(а + вi) (с + di) = ac + adi + bci + bdi2 = (ac - bd) + (ad + bc)i
Пример: (4 - 3i) (-2 + 5i) = (-8 + 15) + (20 + 6)i = 7 + 26i
3. Алгебраическая форма комплексного числа.
Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а - действительная часть, bi - мнимая часть, причем b - действительное число.
Комплексное число a + bi считается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0
Комплексное число a + bi при b = 0 считается совпадающим с действительным числом a: a + 0i = a.
Комплексное число a + bi при a = 0 называется чисто мнимым и обозначается bi: 0 + bi = bi.
Геометрическое изображение комплексных чисел.
Как известно, действительные числа можно изображать точками числовой прямой. При этом каждому действительному числу соответствует единственная точка числовой прямой. Верно и обратное утверждение: каждой точке числовой прямой соответствует единственное действительное число. Значит, между точками числовой прямой и множеством всех действительных чисел установлено взаимно однозначное соответствие.
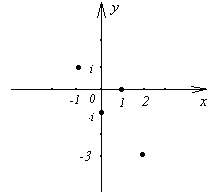
Подобно тому, как действительные числа изображаются точками числовой прямой, комплексные числа можно изображать геометрически точками плоскости. Каждому комплексному числу а + вi поставили в соответствие точку плоскости с координатами А(а; в).
Множество всех комплексных чисел находится во взаимно-однозначном соответствии с множеством всех точек плоскости. К любой точке плоскости можно провести радиус-вектор. Ось ОХ - действительная ось; ОУ - мнимая ось.
Пример. Постройте точки, изображающие комплексные числа: 1; - i; - 1 + i; 2 - 3i .
Студент выходит к доске
Пример 1. Найти сумму чисел и .
Решение: по правилу сложения комплексных чисел имеем:
.
Пример 2. Найти произведение чисел и .
Решение: по правилу умножения комплексных чисел имеем:
.
Пример 3. Найти произведение чисел и .
Решение: по правилу умножения комплексных чисел имеем:
.
III. Домашнее задание.
Дома учащимся предлагается выполнить задание на повторение и закрепление пройденного материала.
Вариант 1.
1. Решите уравнения.
а) x2 - 4x + 5 = 0;
Вариант 2.
1. Решите уравнения.
а) x2 + 6x + 12 = 0;
IV. Подведение итогов урока.