Конспект урока по теме Функции и их графики (7 класс)

Тема урока: «Функции и их графики»

Цель урока:

• организовать деятельность обучающихся по закреплению и применению темы «Функции и их графики»

• развивать образное и логическое мышление на уроке

• воспитывать интерес к предмету

Тип урока: комбинированный (закрепление + применение)

Оборудование: мультимедийное оборудование, карточки, раздаточный материал

Ход урока

1. Организационный момент

Здравствуйте! Садитесь. Записали число, классная работа. Давайте начнем урок с разгадывания ребусов. Слайд1

Кто мне назовет тему нашего урока? «Функции и их графики» Слайд2

А как вы дамаете какой будет цель нашего урока?

Закрепление и применение знаний по теме «Функции и их графики»

2. Актуализация знаний

Математический диктант, закончите фразу

1. Зависимость одной переменной от другой, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной, называется …

2. Значение независимой переменной - это …

3. Значение зависимой переменной - это …

4. Переменная, значения которой выбираются произвольно, называется …

5. Все значения, которые принимает независимая переменная - это …

6. Переменная, значения которой определяются выбранными значениями независимой переменной, называется …

7. Множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции, называется

8. Все значения, которые принимает зависимая переменная - это …

Слайд 3 ответы

В лист самооценки поставьте себе отметку за этот вид работы

4-5 заданий - «3»

6-7 заданий - «4»

8 заданий - «5»

3. Закрепление и применение знаний

А теперь поработаем с функциями. Слайд 4

№1 Даны графики. Являются ли они функциями. В тетрадях пишем номер графика и отвечаем на вопрос «ДА» или «НЕТ»

1)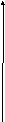

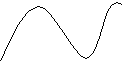
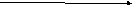
2)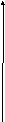

3)

4)

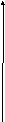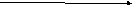5)

Оценили соседа по парте и поставили отметки в лист самооценки.

№2 Работаем в парах. Функция g(x) задана графом: (работа в парах)

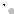
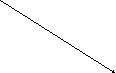
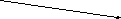
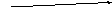
Заполните пропуски:

1. g(3)= ____

2. g(-2)= ____

3. g(x)= 0, если x= _____

4. g(x)= 2, если x= _____ или x= ______

5. D(g): _________________________

6. E(g): _________________________

Самооценка, отметку ставят в лист самооценки №2 Слайд 5

3-4 верных ответа - «3»

5 верных ответов - «4»

6 верных ответов - «5»

№

Y3 Индивидуальная работа на карточках (один ученик у доски на отвороте)

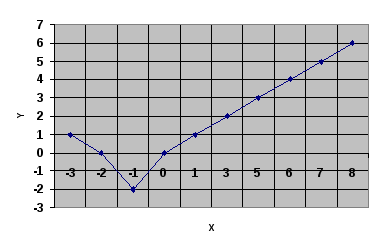
X

Пользуясь графиком, закончите запись:

1. Если x=-1, то y= _______

2. Если аргумент равен 3, то значение функции равно _______

3. y= 0 при x= ______ и при x= _______

4. Если значение функции равно 5, то значение аргумента равно _______

5. Наибольшее значение функции равно ___________, причем это значение функция принимает при x= _________

6. Наименьшее значение функции равно __________, причем это значение функция принимает при аргументе, равном __________

7. Функция принимает отрицательные значения при __________________

8. Функция принимает положительные значения при _________________ и при ________________

9. D(f): _____________________________

10. E(f): _____________________________

Взаимопроверка в карточке отметку и в лист самооценки отметку Слайд6

3-5 верных ответа - «3»

6-8 верных ответов - «4»

9-10 верных ответов - «5»

4. Практическая работа (применение знаний) по вариантам

Вариант I

График функции f(x) ломаная ABCD, где A(-7;-2); B(-3;-2); C(1;2); D(5;-6).

1. Постройте график функции.

2. Заполните пропуски:

f(-6)= ___

f(-3)= ___

f(-1)= ___

f(2)= ____

f(x)= -4, тогда x= ____

f(x)= 0, тогда x= _____ или x=_____

D(f): ____________________________

E(f): ____________________________

3. Запишите в кружках букву И, если высказывание истинно, и букву Л, если оно ложно:

f(-5)= f(-4)

f(4)= f(5)

f(1)< 2

f(3)<0

Точка (-5;5) принадлежит графику

График функции не проходит через точку (6;-8)

4. Сравните значения:

f(0) 0

f(3,5) 0

f(2) f(-2)

Вариант II

График функции f(x) ломаная ABCD, где A(-5;4); B(1;-2); C(3;2); D(8;2).

1. Постройте график функции.

2. Заполните пропуски:

f(6)= ___

f(3)= ___

f(2)= ___

f(-1)= ____

f(x)= 3, тогда x= ____

f(x)= 0, тогда x= _____ или x=_____

D(f): ____________________________

E(f): ____________________________

3. Запишите в кружках букву И, если высказывание истинно, и букву Л, если оно ложно:

f(5)= f(4)

f(-4)= f(-5)

f(1)> 2

f(-3)>0

Точка (5;4) принадлежит графику

График функции не проходит через точку (2;8)

4. Сравните значения:

f(0) 0

f(3,5) 0

f(2) f(-2)

5. Итоги урока, рефлексия

Найдите среднее арифметическое отметок в листе самооценки и поставьте себе отметку за урок.

На листах самооценки допишите несколько фраз:

1. сегодня я узнал…

2. было интересно…

3. было трудно…

4. теперь я могу…

5. я научился…

6. я смог…

7. я попробую…

6. Домашнее задание

написать на доске во время практической работы

Дидактический материал стр.30

По желанию

Доклад на любую из тем:

1. Функция вокруг нас

2. Функция в физике и геометрии

3. Из истории возникновения функции