Технологическая карта урока математики в 6 классе Уравнение

ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА МАТЕМАТИКИ, 6 КЛАСС

1. Бухарова Лидия Николаевна

2. РТ, г. Казань, Советский район, МАОУ «Школа №141»

3. Учитель математики.

4. Математика.

5. 6 класс

6. Решение уравнений. Первый урок в теме.

7. Г.В.Дорофеев, Л.Г. Петерсон. «Математика 6 класс»

8. Цель урока: сформировать способность к решению уравнений; повторить и закрепить: действия с рациональными числами, решение уравнений на нахождение неизвестного множителя, перевод смешанного числа в неправильную дробь и обратно.

9. Формируемые метапредметные результаты:

• личностные универсальные учебные действия: умение правильно излагать свои мысли, понимать смысл поставленной задачи;

• Регулятивные универсальные учебные действия: умение самостоятельно ставить новые учебные задачи путем задавания вопросов о неизвестном, планировать собственную деятельность, определять средства для ее осуществления;

• Познавательные универсальные учебные действия: умение извлекать необходимую информацию из прослушанного материала, структурировать информацию в виде записей выводов и определений

10. Тип урока: урок открытия новых знаний.

11. Формы работы учащихся: фронтальная, индивидуальная.

12. Необходимое техническое оборудование: доска, проектор, экран, компьютерный класс.

СТРУКТУРА И ХОД УРОКА.

Этап урока

Деятельность учителя

Деятельность учащихся

Формируемые УУД

1

Самоопределение к учебной деятельности

Цель этапа:

1) включить учащихся в учебную деятельность;

2) определить содержательные рамки урока: продолжить работать с уравнениями.

- Здравствуйте, ребята! Что мы повторили на прошлом уроке?

- Сегодня на уроке мы будем решать уравнения

Учащиеся готовы к началу работы.

Отвечают: понятие уравнения, корня уравнения, узнали, что значит решить уравнение. Раскрывают основные понятия.

Личностные УУД:

проявлять интерес к новому содержанию, осознавая неполноту своих знаний

Познавательные УУД:

формулировать информационный запрос

Регулятивные УУД:

определять цели учебной деятельности

2

Актуализация знаний и фиксация затруднения в индивидуальной деятельности

Цель этапа:

1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: решение простейших уравнений;

2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;

3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;

4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний: понятие уравнения.

1. Не решая, найдите те пропорции, неизвестный член которых отрицательное число, и те, неизвестный член которых положительное число:

;

- Проверьте себя, вычислив. (-2;0,05;-2;-40)

- Назовите самый маленький корень из полученных результатов. Измените уравнение так, чтобы корень уравнения стал числом положительным. (-40; один из примеров ).

2. Сравните уравнения. Верно ли утверждение, что каждая пара уравнений имеет одинаковые корни? Докажите.

1) 3)

;

2) 4)

; .

Последняя пара уравнений вызовет затруднение.

Предложить обучающимся найти корни уравнения, используя программу «Максима» на компьютере. На доске напоминание записи арифметических действий:

1.Войти в программу «Максима»

2. «Уравнение»

3. Solve

«•» * умножение

«:» / деление

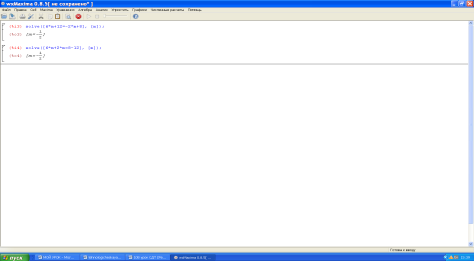
По каждой пропорции отвечает один ученик, обосновывая ответ правилом умножения и деления рациональных чисел.

Объясняет один ученик - одно уравнение: первая и третья пары имеет одинаковые корни, так как по методу «весов», если в равенстве увеличить или уменьшить на несколько единиц или в несколько раз правую и левую часть, то равенство не изменится: в первом уравнении левую и правую часть увеличили в 4 раза, в третьем уравнении увеличили на 2.

Во втором уравнении, упростив левую часть, получим -6x, т.е. вторая пара имеет одинаковые решения.

Учащиеся получают корень -0,5

Последняя пара уравнений вызовет затруднение.

Решают уравнение с помощью программы «Максима»

Личностные УУД: мотивация учения; оценивание усваиваемого содержания;

Регулятивные УУД:

планировать, т.е. составлять план действий с учетом конечного результата.

Познавательные УУД: анализ с целью выделения признаков, выбор оснований и критериев для сравнения; построение логической цепи рассуждений; выдвижение гипотез и их обоснование.

3

Выявление причины затруднения и постановка цели деятельности

Цель этапа:

1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;

2) согласовать цель и тему урока.

- Почему последняя пара уравнений вызвала затруднение? (Для того чтобы ответить на вопрос, надо решить оба уравнения, потому что для них не использовали ранее известные методы

упрощения.)

- Перечислите все известные методы решения уравнений.

На доске:

1. Правила нахождения

неизвестных компонент

арифметических

действий.

2. Основное свойство пропорции.

3. Метод «весов».

4. Метод проб и ошибок.

5. Метод перебора.

- А может быть такое, что использованы какие-то новые способы, но мы их ещё не знаем? (Да, может.)

- Какую цель мы можем поставить перед собой? (Выяснить, не использованы ли новые методы, и если использованы, то понять, что это за метод.)

- Какова тема урока? (Решение уравнений.)

Учащиеся перечисляют.

Отвечают на вопрос.

Ребята формулируют цель, объявляют тему урока и записывают тетради: « Решение уравнений».

Регулятивные УУД:

определять цели учебной деятельности

Познавательные УУД:

формулировать информационный запрос

4

Построение проекта выхода из затруднений

Цель этапа:

1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;

2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.

- Запишите уравнения в тетрадь.

- Какой метод вы можете использовать для того, чтобы решить уравнение? (Метод «весов».)

Подробно на доске решаются уравнение:

6m + 12 + 2m = -2m + 2m + 8; 8m = -4;

8m + 12 = 8; m = -4 : 8;

8m + 12 - 12 = 8 - 12; m = -0,5.

8m = -4;

m = -4 : 8;

m = -0,5.

- Мы еще раз убедились, что уравнения имеют одинаковые решения.

- Давайте проанализируем решение первого уравнения.

6m + 12 + 2m = -2m + 2m + 8;

6m + 2m + 12 = 8.

- Сравните это уравнение с данным, что произошло?

- Используя какой метод, мы это получили?

8m + 12 - 12 = 8 - 12;

8m = 8 - 12

- Что здесь произошло?

- Чем отличается метод «весов» от нового метода?

- При использовании этих методов результат получаем один и тот же? (Да.)

- Какой метод быстрей приводит к результату? (Второй.)

- Сформулируйте новый способ решения уравнения.

На доске:

Слагаемые можно переносить из одной части в другую,

меняя знак на противоположный.

Учащиеся объясняют в чем заключается метод «весов»

Отвечают:

-2m стояло справа, а теперь стоит слева, но со знаком «+».

- Метод «весов».

- 12 стояло слева со знаком «+», а теперь стоит справа со знаком «-».

- В методе «весов» мы увеличивали или уменьшали правую и левую часть уравнение на одно и то же число, в новом методе переноси или числа из одной части уравнения в другую, меняя знак переносимого слагаемого на противоположный.

Учащиеся формулируют.

Познавательные УУД:

извлекать необходимую информацию из прослушанных текстов;

структурировать знания;

Коммуникативные УУД:

вступать в диалог, с достаточной полнотой и точностью выражать свои мысли.

Предметные УУД:

давать определения новым понятиям темы;

называть способы решения уравнения.

5

Первичное закрепление во внешней речи

Цель этапа:

зафиксировать изученное учебное содержание во внешней речи.

№ 87 (г, ж) - у доски.

г) 4n = -2 + 6n + 7; ж) ;

4n - 6n = -2 + 7 ;

-2n= + 5;

n = 5: (-2)

n = -2,5

ж) ;

;

;

m = -5,64.

№ 87 (е, и) - в парах с проверкой по образцу.

Образец выполнения задания в парах (проектор)

е) -3d - 10 = 3d - 6;

-3d - 3d = - 6 +10;

-6d = 4;

d = -

и) ;

;

;

х = 0,1

Осмысливают и приступают применять новый способ решения на практике.

Два ученика у доски решают уравнения с комментариями.

Один учащийся (быстро справившийся с двумя уравнениями из класса) решает уравнения на компьютере, запись уравнения и ответы демонстрируются классу)

Один учащийся (быстрее справившийся с двумя уравнениями) решает уравнения на компьютере, решение и ответы демонстрируются классу)

Предметные УУД:

Различать способы решения уравнений, правильно формулировать ход решения уравнений, находить неизвестные компоненты, применять на практике полученные выводы

Познавательные УУД:

анализировать и сравнивать объекты, подводить под понятие;

Коммуникатитвные УУД: эффективно сотрудничать и способствовать продуктивной кооперации

6

Самостоятельная работа с самопроверкой по эталону

Цель этапа:

проверить своё умение применять новое учебное содержание в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.

№ 87 (д, з)

д) 2 - с = 5с + 1

з) -1,6 - 0,3p = 0,9p + 0,2;д) 2 - с = 5с + 1;

-с - 5с = 1 - 2;

-6с = -1;

с = -1 : (-6);

с =

Ответ:

Слагаемые можно переносить из одной чисти в другую,

меняя знак на противоположный.

ax = b

x = b : a

з) -1,6 - 0,3p = 0,9p + 0,2;

-0,3p - 0,9p = 1,6 + 0,2;

-1,2p = 1,8;

p = -1,5

Ответ: -1,5.

Учащиеся сначала проверяют ответ на компьютере, если ответ не совпадает, проверяют решение по эталону (карточка)

Анализируют и исправляют ошибки.

Предметные УУД: отрабатывают умение решать уравнения новым способом;

Личностные УУД: умение понимать смысл поставленной задачи;

Познавательные УУД: извлекать необходимую информацию из прослушанного материала

7

Включение в систему знаний и повторение

Цель этапа:

1) тренировать навыки использования нового содержания совместно с ранее изученным: решение уравнений методом пропорции, методом перебора, методом проб и ошибок;

2) повторить учебное содержание, которое потребуется на следующих уроках: нахождение значений числовых выражений.

№ 90 (а)(свойство пропорции)

;

- 600 = 360 - 160а;

160а = 960;

а = 6.

№ 91 (а)(метод перебора)

7х(9 - 2х) = 70;

14

35

70

10

5

2

1

№ 92 (а)(метод проб и лшибок)

х (х + 8) = 33

х = 3

№ 103.(найти значение выражения)

а) -4; б) -5; в) -15; г) 1,4 д) -8; е) .

Учащиеся решают уравнения самостоятельно, первые три учащихся справившиеся с заданиями показывают свое решение учителю на оценку. Решения проецируются, остальные проверяют свое решение.

Регулятивные УУД: осознание качества и уровня усвоения ранее изученного;

Познавательные УУД: самостоятельное создание способов решения проблем творческого характера.

8

Рефлексия деятельности

Цель этапа:

1) зафиксировать новое содержание, изученное на уроке;

2) оценить собственную деятельность на уроке;

3) поблагодарить одноклассников, которые помогли получить результат урока;

4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;

5) обсудить и записать домашнее задание.

Организация учебного процесса на этапе 8:

- Что нового вы сегодня узнали?

- Какой способ вам помог вывести новый способ решения уравнений?

- Какие преимущества у нового способа решения уравнения?

- С какими трудностями вы столкнулись при применении нового способа?

- Проанализируйте свою работу на уроке

Учащиеся отвечают на вопросы. Высказывают свое мнение о вновь изученном способе решения уравнений, его преимуществах.

Определяют, какие знания необходимы для применения нового способа.

Оценивая свою работу на уроке, высказывают все ли у них получилось, все ли было понятно.

Регулятивные УУД:

констатировать необходимость продолжения действий

Познавательные УУД:

решать различные виды уравнений

Коммуникативные УУД:

адекватно отображать свои чувства, мысли в речевом высказывании

Домашнее задание

п. 3.3.5.; № 106 (а, в, д, з); 107 (одно на выбор); 108.

Ребята записывают домашнее задание в дневниках. Просматривают задание в учебнике, если есть вопросы задают их.

Личностные УУД: оценивание усваиваемого содержания.