Урок -игра по теме "Производная и ее применение к исследованию функций"

Разработала Курочкина В.М.

Цель: в игровой форме обобщить и закрепить материал по теме "Производная и ее применение к исследованию функций"

Оборудование: секундомер или песочные часы; плакаты к заданиям №№1, 2, 5, 6; оформление для доски.

В классной комнате, где будет проводится игра должно быть организовано место для рассаживания двух команд таким образом, чтобы члены одной команды могли свободно общаться друг с другом и делать записи.

Ход игры.

Перед началом учитель предлагает группе разделиться на 2 команды.

Для достижения конечной цели командам необходимо собрать 4 ключа. Ключ выдается после успешного прохождения того или иного испытания. Порядок прохождения испытаний таков: команда №1 выбирает номер испытания для команды №2 (при этом содержание испытаний неизвестно игрокам). Ведущий объясняет, в чем заключается соответствующее задание. Заслушав ответ команды №2, противоположная команда должна сказать правильно или неправильно дан ответ. Верность ответов обеих команд оценивает ведущий. В том случае, если команда-рецензент дает неверную рецензию, ей начисляются штрафные очки. Для получения ключа команде, проходящей испытание, необходимо также верно ответить на вопрос, который обязана задать команда-рецензент. Затем команды меняются местами, т.е. отвечающая команда становится рецензентом, а команда-рецензент отвечает на вопросы.

Конечной целью команд является сундучок с кладом (призовым фондом). Если в ходе испытаний только одна команда собрала необходимое количество ключей, то весь призовой фонд отдается этой команде. Если обе команды собрали по 4 ключа, то призовой фонд делится пополам. Если ни одна из команд не набрала нужного количества ключей, призовой фонд сокращается.

1 испытание

Из 4 плакатов надо выбрать тот, на котором записано уравнение функции, невозрастающей на всей области определения. Свой ответ необходимо аргументировать.

Решение все члены команды обсуждают совместно, но для ответа у доски вызывается только один из участников команды, которого выбирает команда-противник.

1) ;

2) ;

3) ;

4) .

Ответ: Заданному условию удовлетворяет функция №3, т.к. для всех .

2 испытание

За 30 секунд продифференцировать все функции (ответы не обязательно упрощать).

Участвует один из членов команды, которого выбирает команда - противник.

1) ;

2) ;

3) ;

4) .

Ответы: 1) ;

2) ;

3) ;

4) .

3 испытание

Построить график функции .

График строят все члены команды на местах, ответ у доски зарисовывает любой член команды. Систему координат для ответа заранее чертит другой участник команды.

4 испытание

Привести пример функции: а) определенной на R (но не линейную),

б) определенной на ;

в) определенную на ;

г) не определенную на R.

Ответ обсуждается всеми членами команды, к доске выходит один ученик, определяемый командой-соперницей. При этом отвечающему у доски нельзя иметь при себе готовые ответы.

5 испытание

Выбрать плакат, на котором изображен график функции, имеющей три стационарные точки.

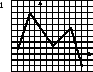
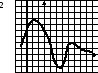
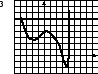
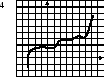
Ответ: плакат №2

6 испытание

Из приведенных функций (см. 5 испытание) выбрать ту, которая имеет только критические точки, но не имеет стационарных.

7 испытание

Найти наибольшее значение функции на .

Ответ: .

8 испытание

Что вы можете сказать о производной функции, которую описывает поговорка "Чем дальше в лес, тем больше дров".

Ответ: производная положительна на всей области определения, т.к. эта функция - монотонно возрастающая.

Перед тем, как открыть ларец с кладом, команда-победительница должна разгадать кодовое слово "Переменная"

Подсказки к кодовому слову:

1) С ее появлением математика перешагнула из арифметики в алгебру;

2) В функции их как минимум две;

3) Бывает зависимой и независимой;

4) Обозначается буквой.

Итог урока: Объявляется команда победитель и награждение.