Тема: Правило вычисления производной частного

Дата 15.11

Тема: Правило вычисления производной частного

Цели:

• Ввести правила дифференцирования производной частного

• Повторить правила нахождения(f(x)+g(x))΄, (f(x)-g(x))΄ и (c f(x))΄

• Учиться применять новое знание при решении задач

• развивать творческую и мыслительную деятельность учащихся

• развивать способность к «видению» проблемы

• формировать умения чётко и ясно излагать свои мысли

• формировать познавательные интересы и мотивы самосовершенствования

• воспитывать умение работать с имеющейся информацией

• воспитывать культуру труда общения, навыки самоконтроля, взаимоконтроля и взаимопомощи

• Ход урока.

• I.Организационный момент. Проверка домашнего задания.

• II. Актуализация опорных знаний.

Мы несколько раз уже использовали слово " производная ".

1. Так, кто скажет определение производной функции в точке?

Ответ: Производной функции в точке Х₀ называется число к которому стремится разностное отношение .

2. Как называется операция нахождения производной ?

Ответ: дифференцированием.

3. При решении каких задач применяется производная?

Ответ при решении задач на нахождении мгновенной

скорости при неравномерном движении тела.

Есть еще другие задачи, где необходимо использовать производную;

Например: При решение квадратного уравнения ах² +вх+с = 0 количество корней определяем с помощью дискриминанта. А если нам потребуется определить количество корней уравнения вида Какими формулами можно здесь воспользоваться? Тут и нам поможет производная. На это мы не будем останавливаться, т.к. при изучении дальнейших тем, вы вернетесь к этой задаче.

Мы вернемся к нашей теме и вспомним правила нахождения производных:

Правило 1 (производная от произведения числа на функцию). Справедливо равенство

(c f (x))' = c f ' (x) ,

где c - любое число.

Другими словами, производная от произведения числа на функцию равна произведению этого числа на производную функции.

На

Правило 2 (производная суммы функций). Производная суммы функций вычисляется по формуле

(f (x) + g (x))' = f ' (x) + g' (x),

то есть производная от суммы функций равна сумме производных этих функций.

Правило 3 (производная разности функций). Производная разности функций вычисляется по формуле

(f (x) - g (x))' = f ' (x) - g' (x),

то есть производная от разности функций равна разности производных этих функций.

Правило 4 (производная произведения двух функций). Производная произведения двух функций вычисляется по формуле

(f (x) g (x))' = f ' (x) g (x) + f (x) g' (x),

Другими словами, производная от произведения двух функций равна производной от первой функции, умноженной на вторую функцию, плюс первая функция, умноженная на производную от второй функции.

1. (U+V)¹

2. (UV)¹

Изучение нового материала

Производная частного равна разности произведения производной числителя на знаменатель и произведения числителя на производную знаменателя, деленной на квадрат знаменателя.

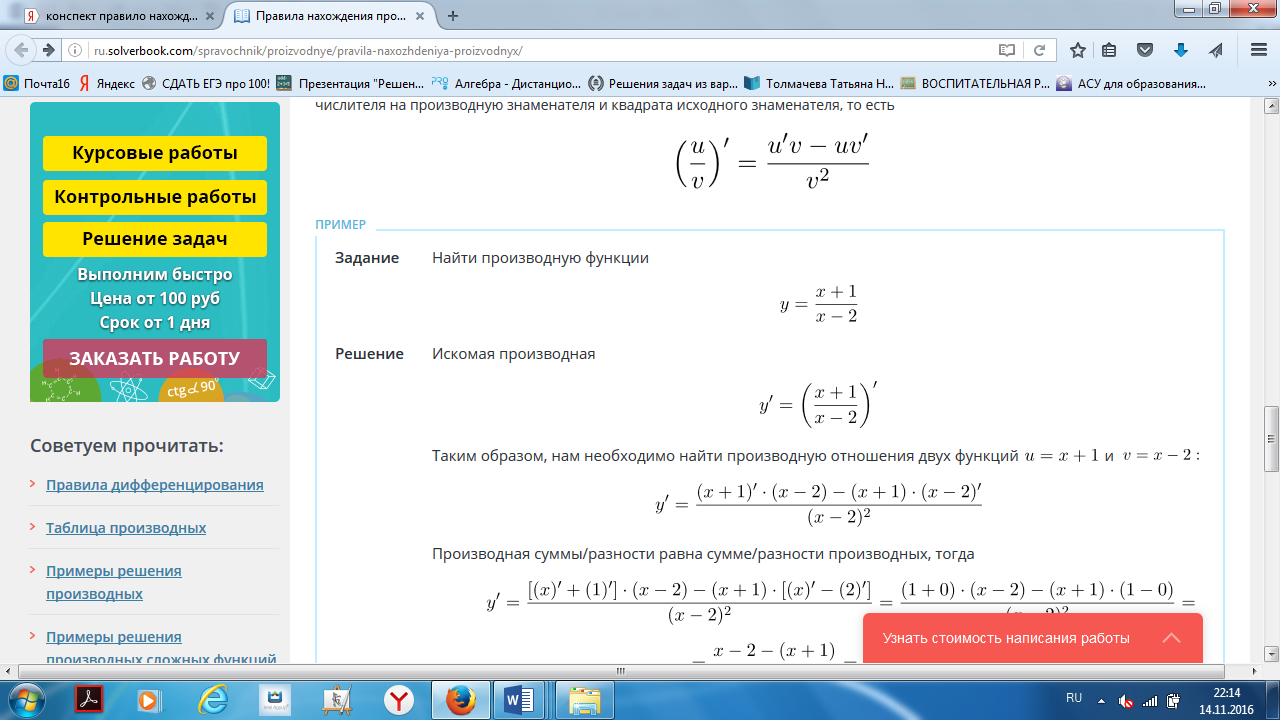
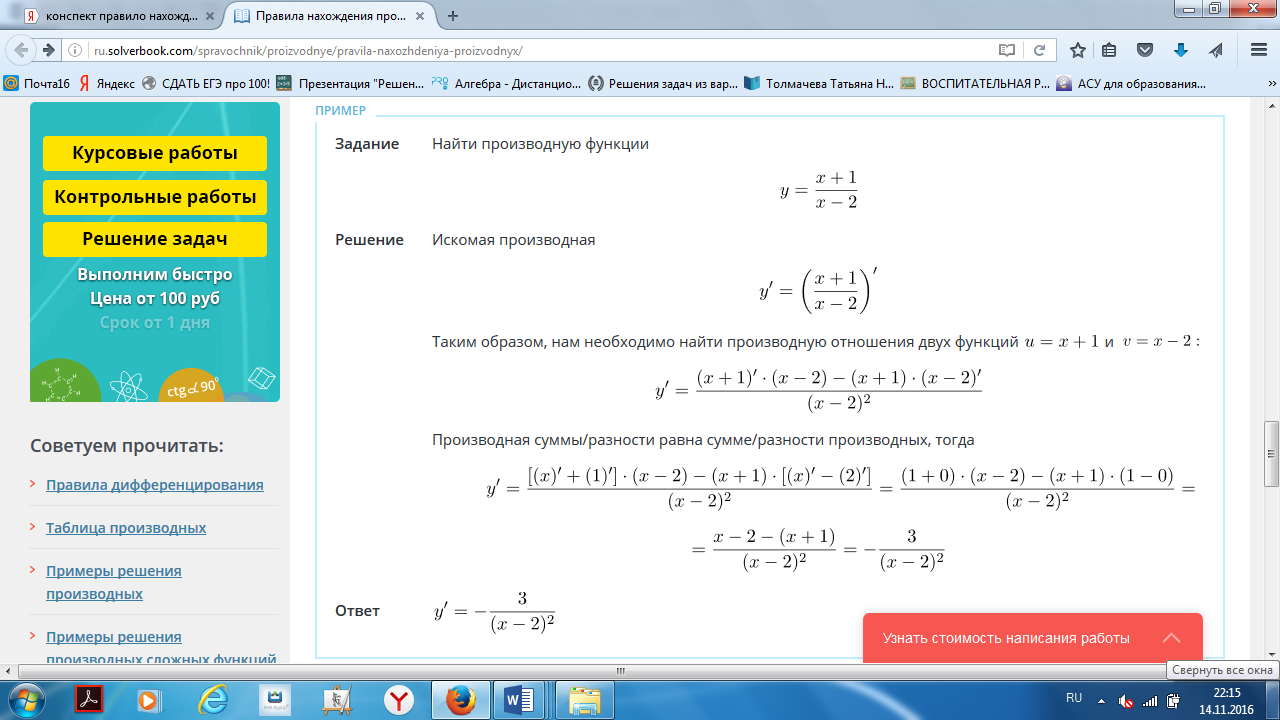
Закрепление изученного материала

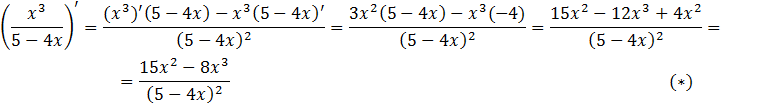
Выполнение №28.18 (работа в группах)

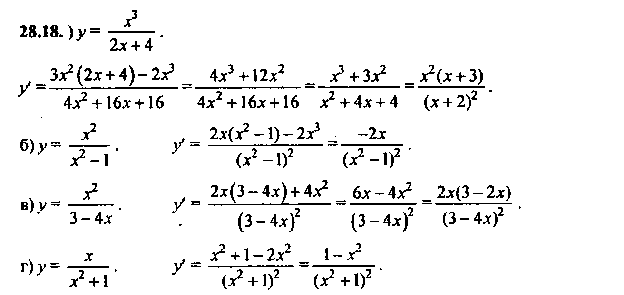
Отработка прототипов заданий №9 нахождение физического смысла производной открытого банка задач ЕГЭ по математике

Задание В9 (№119979)

Материальная точка движется прямолинейно по закону , где - расстояние от точки отсчета в метрах, - время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?

Решение.

Найдем производную функции :

По условию, скорость точки равна 2 м/с, значит, значение производной в момент времени равно 2.

Получаем уравнение:

Решим его:

, - не подходит по смыслу задачи: время не может быть отрицательным.

Ответ: 7

Решим задание В9 (№ 119975) из Открытого банка заданий для подготовки к ЕГЭ по математике.

Материальная точка движется прямолинейно по закону , где - расстояние от точки отсчета в метрах, - время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени .

Решение.

1. Найдем производную функции :

2. Найдем значение производной в точке :

Ответ: 60 м/с.

Рефлексия

Выберите 1 фразу для соседа по парте:

Ты молодец.

Я доволен твоей работой на уроке.

Ты мог бы поработать лучше.

Домашнее задание:

Повторить основные правила дифференцирования

карточки

</<br>