Урок по геометрии 10 класс

Урок 10

Тема: «Решение задач на применение теорем Чевы и Менелая».

Создать условия для того, чтобы учащиеся могли научиться применять теоремы Чевы и Менелая при решении задач

Основное содержание темы, термины и понятия

Треугольник, пропорциональные отрезки в треугольнике, теорема Чевы, теорема Менелая.

Планируемый результат

Предметные умения

Универсальные учебные действия

Предметные: усвоение систематических знаний о треугольниках, формулировать и доказывать теоремы Чевы и Менелая и использовать их при решении задач

Познавательные: умение понимать и использовать математические средства наглядности, для иллюстрации, интерпретации, аргументации.

Регулятивные: умение самостоятельно планировать альтернативные пути достижения целей.

Коммуникативные: выстраивают аргументацию, участвуют в диалоге, приводят примеры.

Личностные: формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики.

Организация пространства

Формы работы

Фронтальная (Ф.); парная (П.); индивидуальная (И.)

Образовательные ресурсы

1. 1. Геометрия. 10-11 классы / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина (М.: Просвещение, 2015).

I этап. Актуализация опорных знаний.

Цель: систематизировать знания учащихся по теме

(Ф).

1). Проверить решение домашней работы. К доске приглашается двое учащихся для доказательства теорем Чевы и Менелая.

2). Пока учащиеся готовятся можно провести опрос по теории ранее повторенных тем.

II этап. Решение задач.

Цель: применять доказанные теоремы при решении задач

(Ф)

Решить задачи:

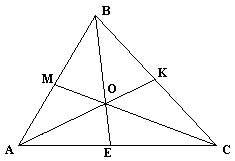
Дано: ABC;

A₁BC; B₁ AC;

C₁ AB. S_ABC= S,

PKN ограничен прямыми:AA₁, BB₁, CC₁.

Найти: S_PKN

Решение:

1 способ

Рассмотрим ACC₁ и секущую BB₁ (точки пересечения B₁, K, B). Применим теорему Менелая .

; из этого следует =3. Подставим в равенство

, отсюда,

Рассмотрим ABA₁ и секущую CC₁ (Точки пересечения C₁, N, C) По теореме Менелая:

; , отсюда, , подставим в равенство, , отсюда,

Рассмотрим BB₁C и секущую AA₁ (точки пересечения A, P, A₁) По теореме Менелая:

; , отсюда, . Подставим в равенство , отсюда,

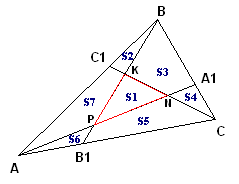
Далее будем использовать свойство площадей частей треугольника

, где DAC

Действительно,

Обратимся к рисунку к задаче

В C₁BC, следовательно, S₃+S₄=6S₂

В AA₁C, следовательно, S₅ +S₆ =6S₄

В ABB₁, следовательно, S₂+S₇=6S₆.

т.к. BA₁ = 2 A₁C, следовательно, S_ABA1 = 2S_AA1C, следовательно, S₁+S₂+S₃+S₇=2S₆+2S₅+2S₄ (1)

т.к. AC₁ = 2BC₁, следовательно, S_ACC1 = 2S_BCC1, следовательно, S₁+S₅+S₆+S₇=2S₂+2S₃+2S₄ (2)

т.к. S_B1BC = 2S_ABB1 (B₁C = 2 B₁A)

S₁+S₃+S₄+S₅=2S₂+2S₆+2S₇ (3)

Сложим равенства (1), (2), (3) почленно:

3S₁+S₂+2S₃+S₄+2S₅+S₆+2S₇=4S₂+4S₄+2S₃+2S₅+4S₆+2S₇.

После упрощения получим:

3S₁=3S₂+3S₄+3S₆; S₁=S₂+S₄+S₆

Из доказанного, что S₃+S₄=6S₂ следует, что , так же и , подставим,

S₁₌ + + т.е. S₁=(S₂+S₃+S₄+S₅+S₆+S₇)=, следовательно, S=7S₁, где S=S_ABC; S₁=S_PKN.

Ответ: S=7S₁

III этап. Решение задач.

Цель: уметь применять доказанные теоремы при решении задач.

(Г).

Для первой задачи предложить второй способ решения.

2 способ

По теореме Менелая:, следовательно, .

Значит, S_C1KB = S_C1BC

Аналогично S_AB1P=S_AB1B, S_A1NC=S_ACA1

По условию A₁C=CB, следовательно, S_ACA1=S_ABC, следовательно, S_A1NC=S_ABC

AB₁=AC, следовательно, S_ABB1=S_ABC, следовательно, S_APB1=S_ABC

C₁B=AB, следовательно, S_C1BC=S_ABC, следовательно, S_C1BK=S_ABC

S_ABC=S_ACA1+S_CC1B-S_A1NC+S_APKC1+S_KPN , пусть S_ABC=S.

S=S+S-S+S+S_KPN

S=S+ S_KPN, откуда S_KPN=(1-)S= S; S_KPN=S

Ответ: S_KPN=S

IV этап. Итог урока. Рефлексия

(Ф/И).

- Какие теоремы доказали на уроке?

- Что вызвало наибольшее затруднение?

(И). Домашнее задание: п. 95, 96 учебника на стр.206-209, решить задачи:

1). Дано: ABCD - четырёхугольник. M - середина AD; N - середина BC. MP=PK=KN

Доказать: ABCD - трапеция;

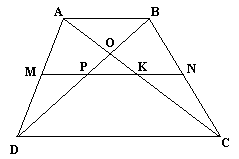
2. Дано: треугольник ABC

Доказать: биссектрисы ABC пересекаются в одной точке