Конспект урока по математике на тему Координатная плоскость (6 класс)

Конспект урока по математике на тему

«Координатная плоскость»

</

Коломна, 2016 г.

План - конспект урока

Предмет - математика

Урок № 1

Тема урока «Координатная плоскость»

Тип урока: изучение нового материала

Деятельностная цель: формирование способности обучающихся к новому способу действия.

Образовательная цель: расширение понятийной базы за счёт включение в неё новых элементов.

Цели:

• ознакомить с прямоугольной системой координат на плоскости;

• научить ориентироваться на координатной плоскости, строить точки по заданным координатам и определять координаты точек, отмеченных на координатной плоскости;

• развивать творческие способности;

• воспитывать интерес к предмету.

Использование современных педагогических технологий: Технология проблемно-диалогического обучения.

Оборудование: Презентация "Координатная плоскость", интерактивная доска, раздаточный материал.

Учебное пособие: Математика- 6, авторы: Виленкин Н.Я. и др.

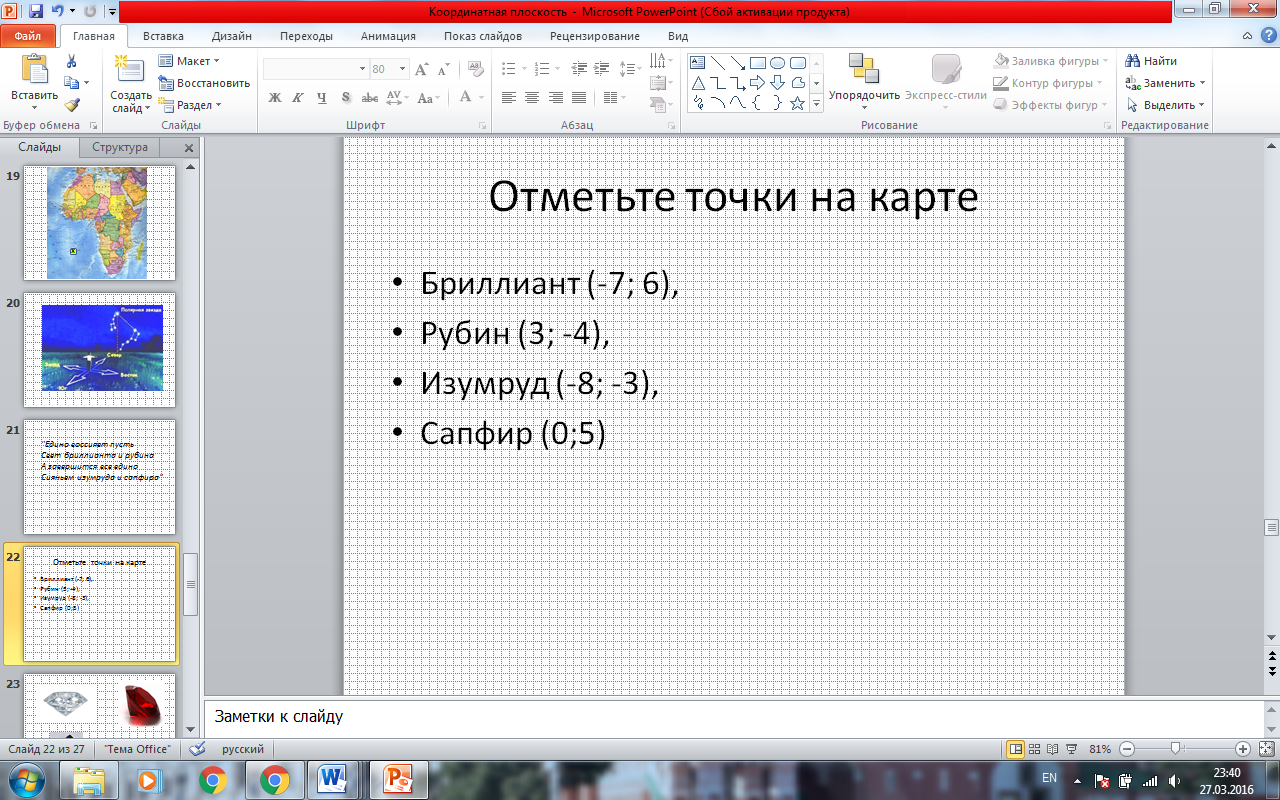
Раздаточный материал: На листочках с готовой координатной плоскостью отметьте точки с заданными координатами, соответствующие названию драгоценностей. Соедините точки попарно и найдите точку их пересечения - место клада.

Бриллиант (-7; 6), Рубин (3;-4), Изумруд (-8;-3), Сапфир (0;5)

Ход урока

I. Организационный момент. Пожелание успеха.

II. Мотивационно-ориентировочная часть

- В речи взрослых вы могли слышать такую фразу: "Оставьте свои координаты". Что означает это выражение? (месторасположение, местонахождение)

- А зачем надо знать чьи-то координаты? (чтобы человека было легко найти)

- Что может послужить координатами? (номер телефона, домашний адрес, место работы, Еmail)

- Суть координат или, как обычно говорят, системы координат состоит в том, что это правило, по которому определяется положение объекта. С различными системами координат мы встречаемся и в нашей повседневной жизни. Давайте попробуем вспомнить:

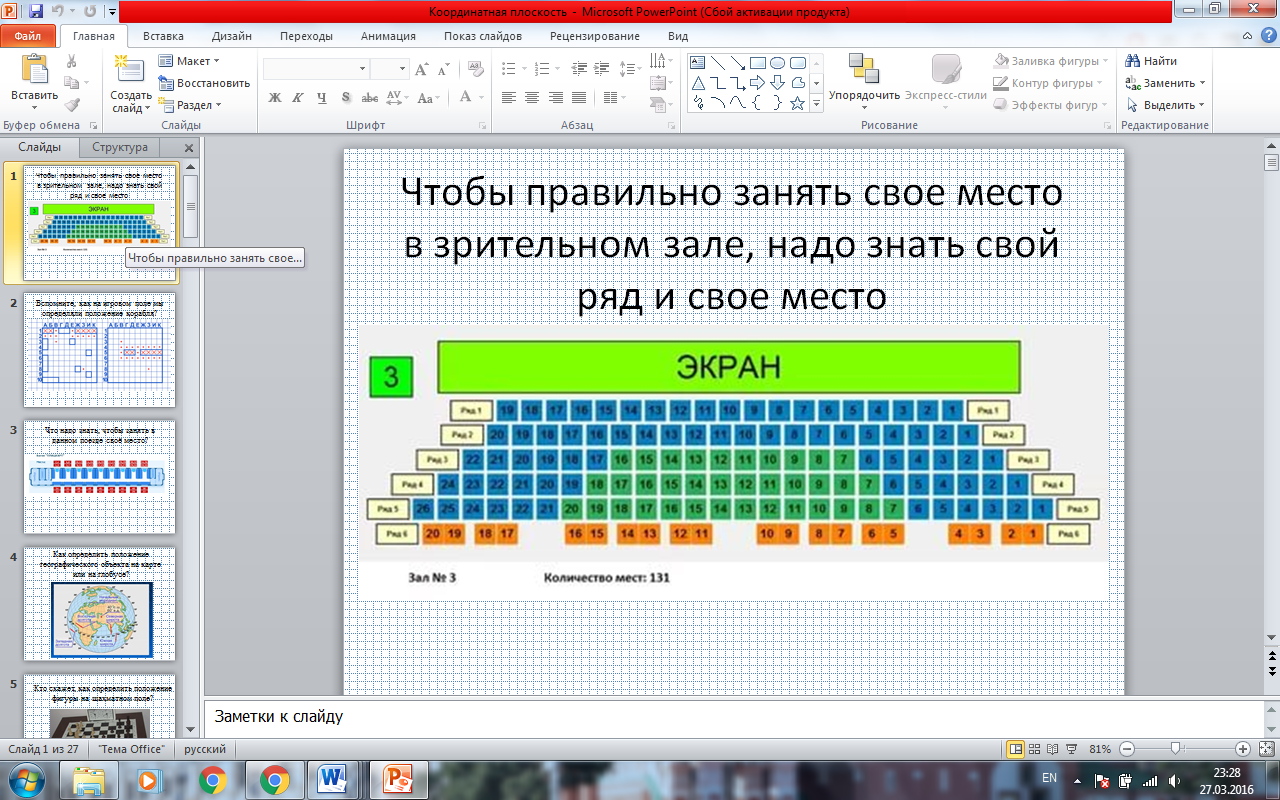
- Что надо знать, чтобы правильно занять своё место в зрительном зале? (ПРИЛОЖЕНИЕ. СЛАЙД 2) (ряд и место в ряду);

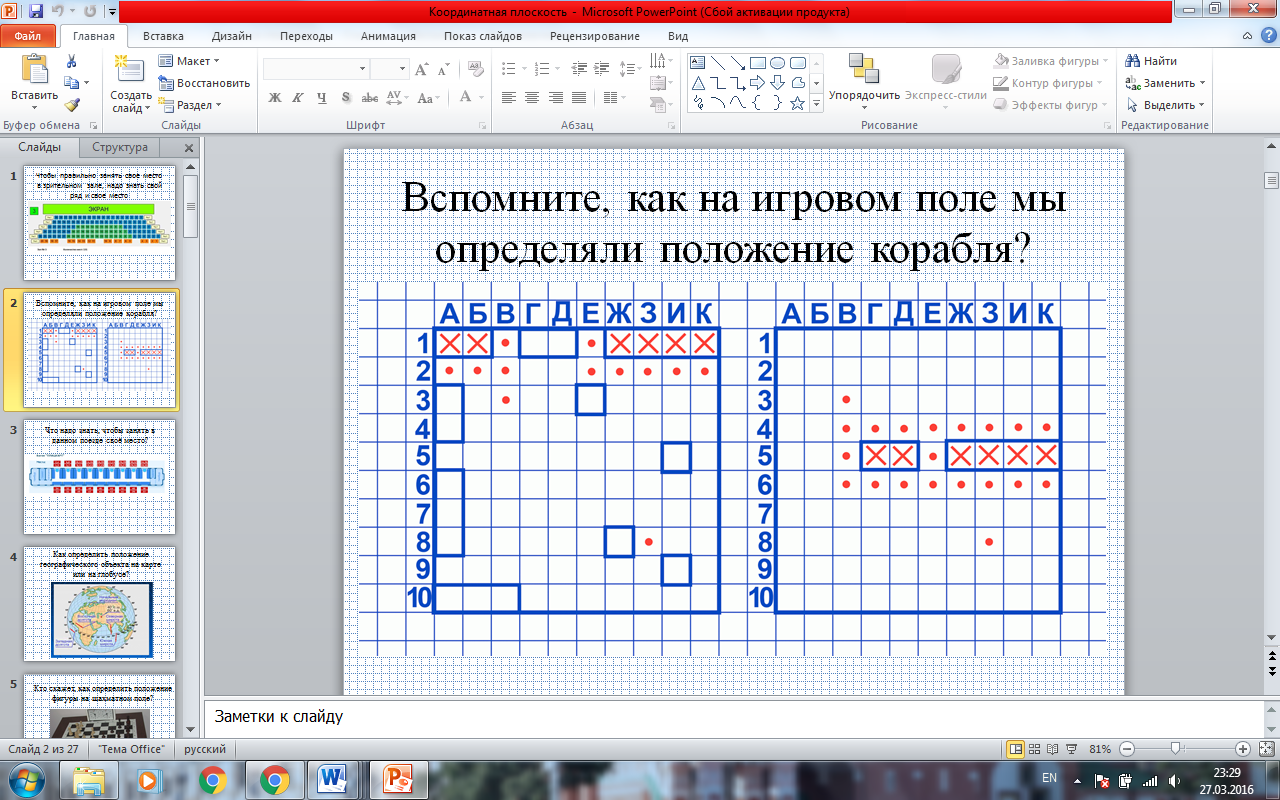
- Во 2 триместре мы проводили урок в форме игры "Морской бой". Вспомните, как на игровом поле мы определяли положение корабля? (двумя координатами - буквой и цифрой); (ПРИЛОЖЕНИЕ. СЛАЙД 3)

- Определите положение этого: корабля.

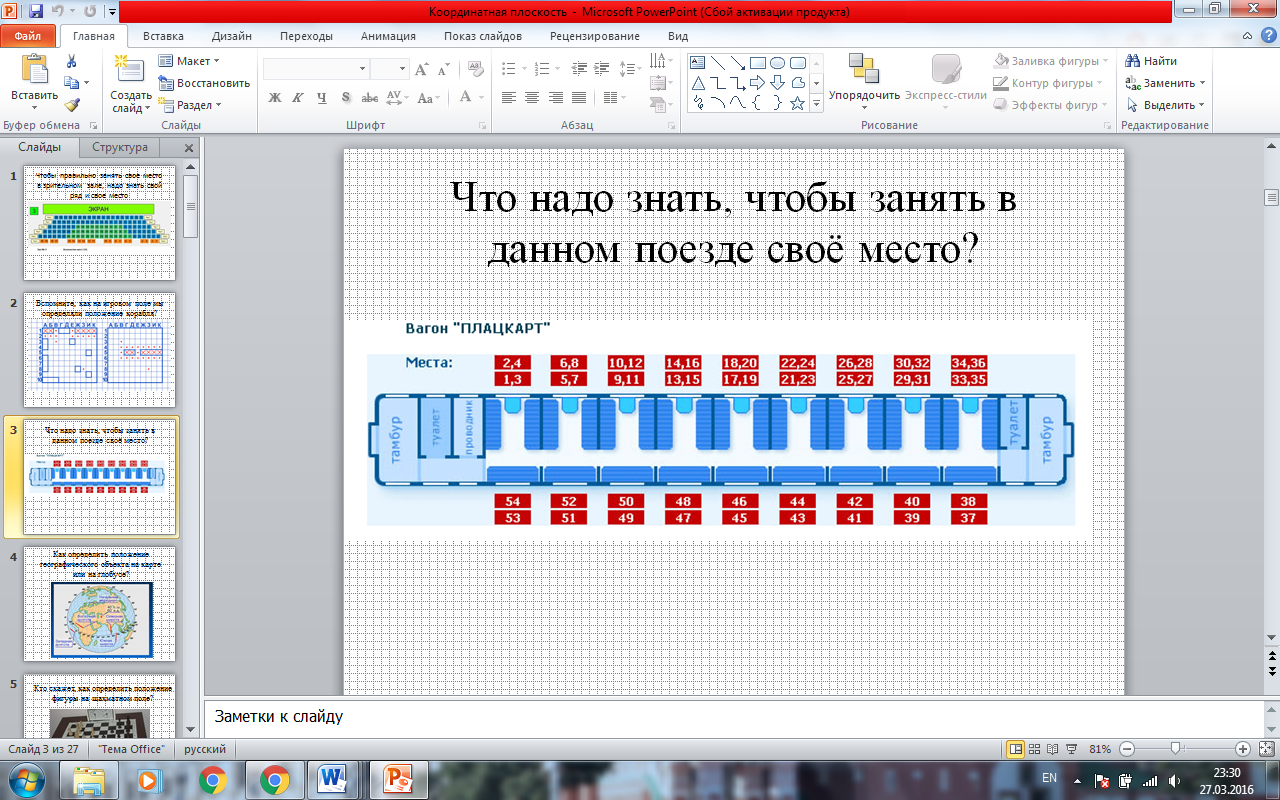
- Что надо знать, чтобы занять в данном поезде своё место? (вагон и место в вагоне); (ПРИЛОЖЕНИЕ. СЛАЙД 4)

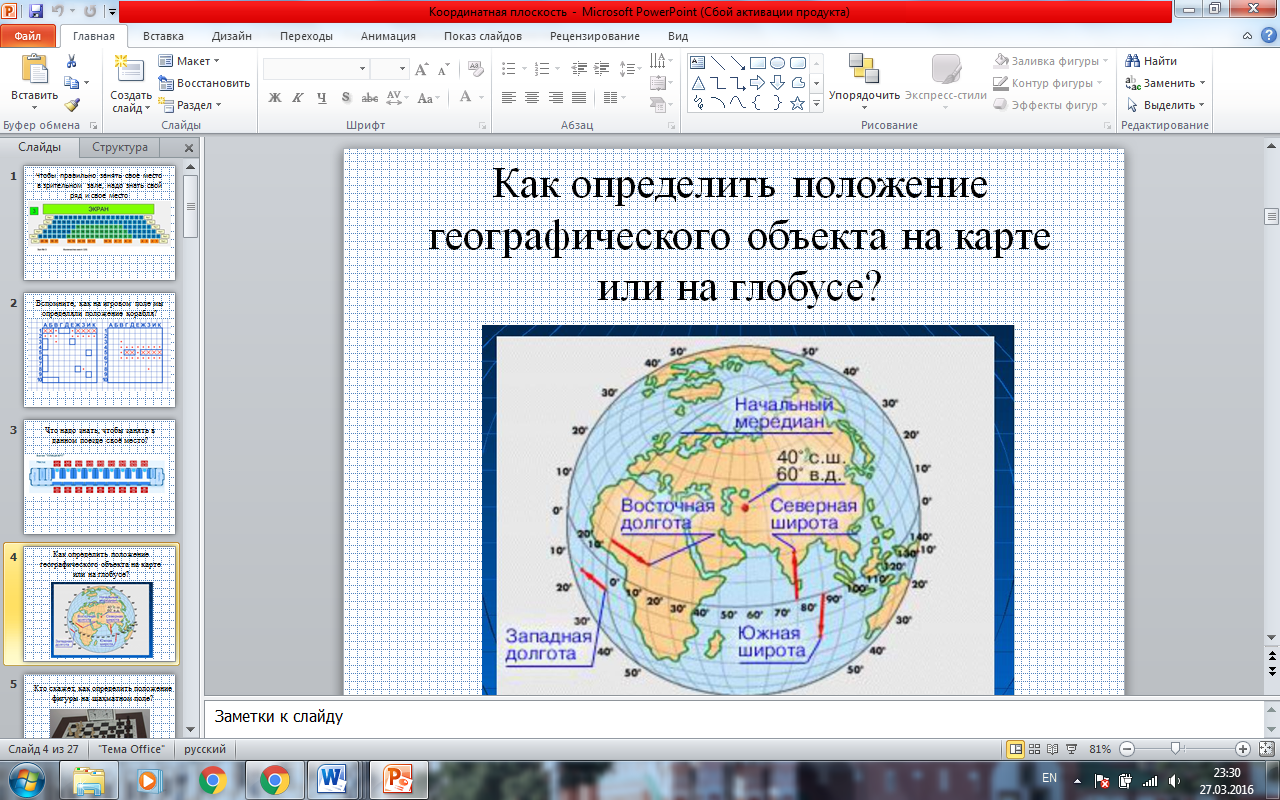
- Как определить положение географического объекта на карте или на глобусе? (определить широту и долготу); (ПРИЛОЖЕНИЕ. СЛАЙД 5)

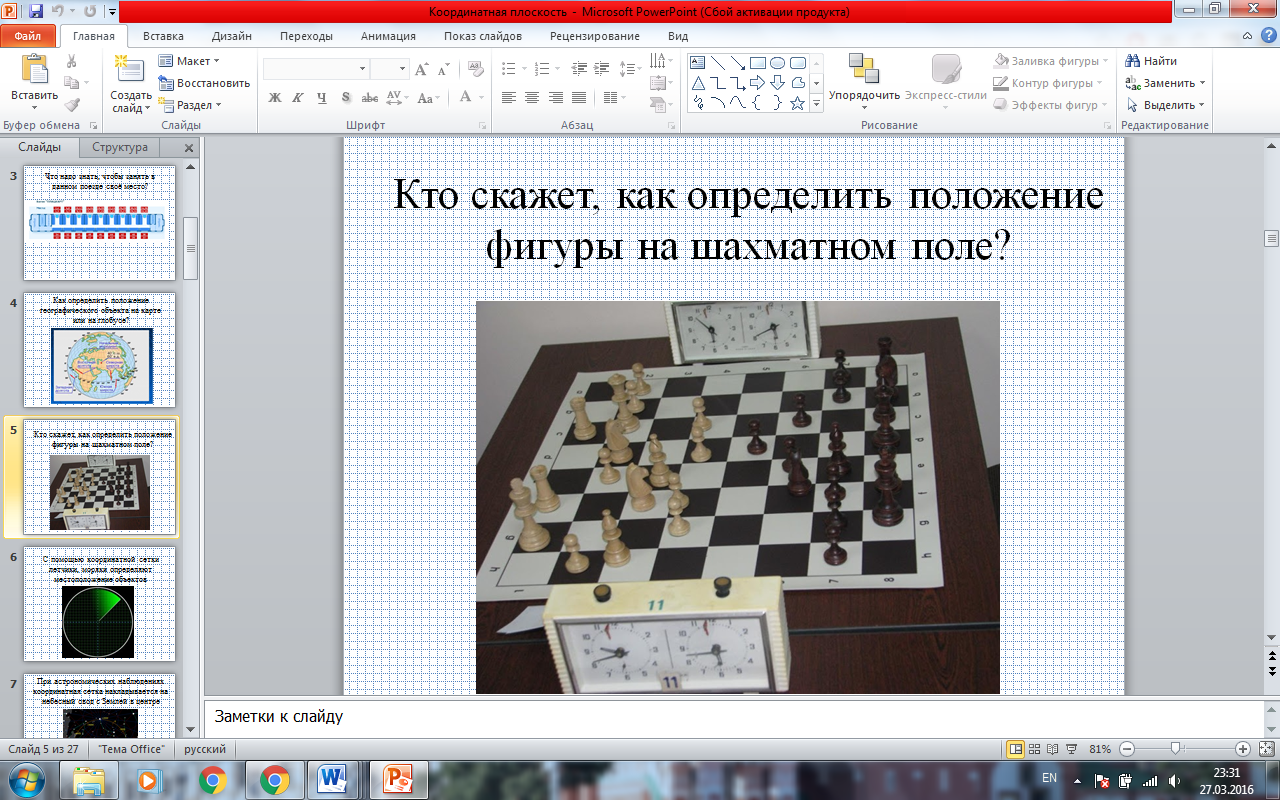
- Кто скажет, как определить положение фигуры на шахматном поле? (ПРИЛОЖЕНИЕ. СЛАЙД 6)

- Определите положение, например, коня.

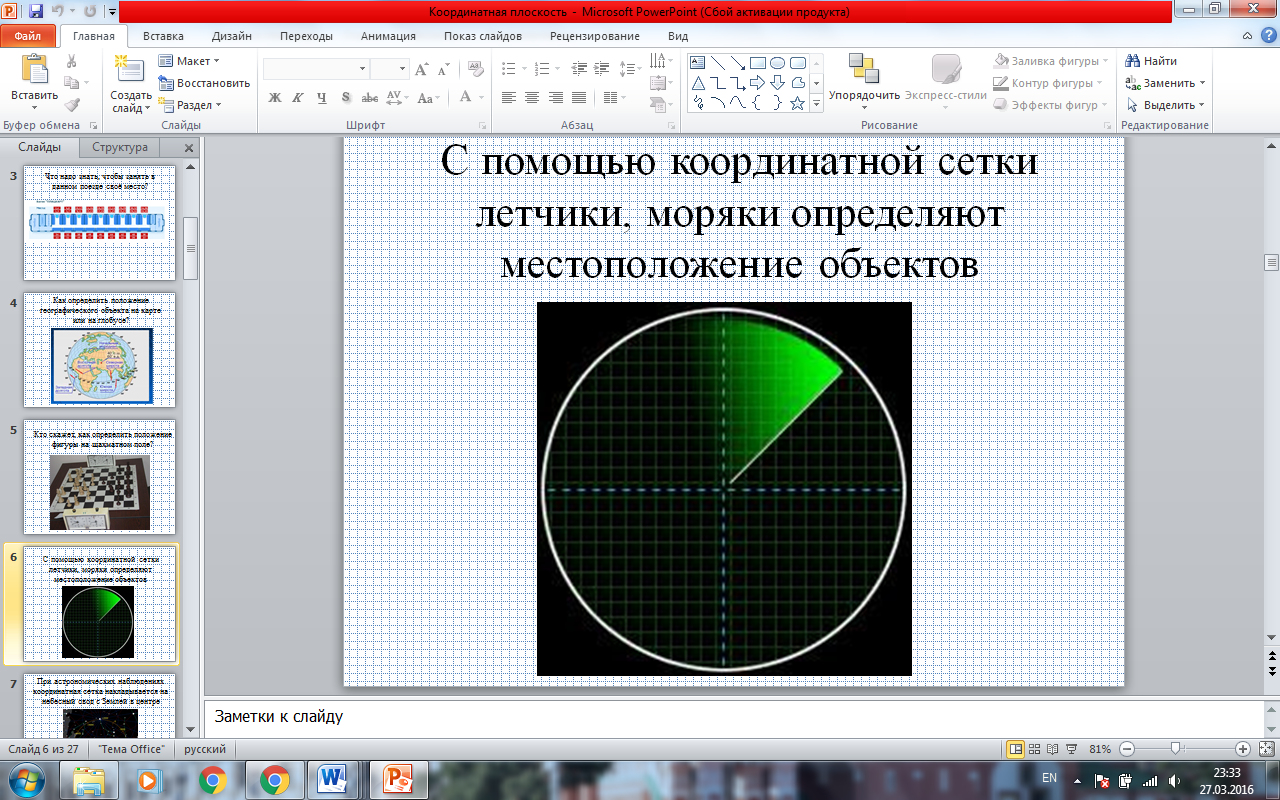
- С помощью координатной сетки летчики, моряки определяют местоположение объектов; (ПРИЛОЖЕНИЕ. СЛАЙД 7)

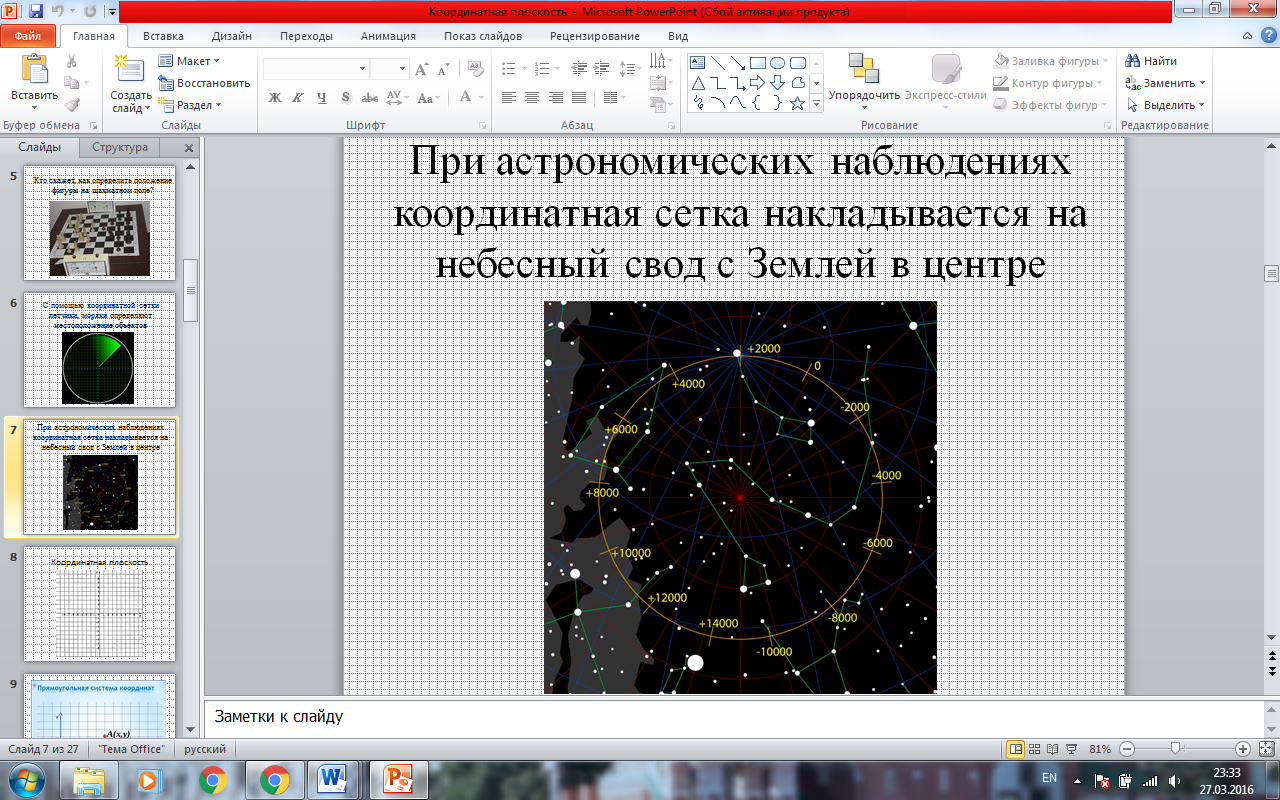
- При астрономических наблюдениях координатная сетка накладывается на небесный свод с Землей в центре. (ПРИЛОЖЕНИЕ. СЛАЙД 8)

Задание: Придумайте систему координат для определения места ученика в классе. Укажите координаты нескольких учеников.

Вы рассмотрели примеры и теперь сделайте вывод: сколько координат надо знать, чтобы определить местоположение того или иного объекта? (две)

III. Введение нового материала.

- Все мы уже знаем, как определить координаты точки на числовой прямой. А кто-нибудь догадался как определить координаты точки на плоскости? (предлагают)

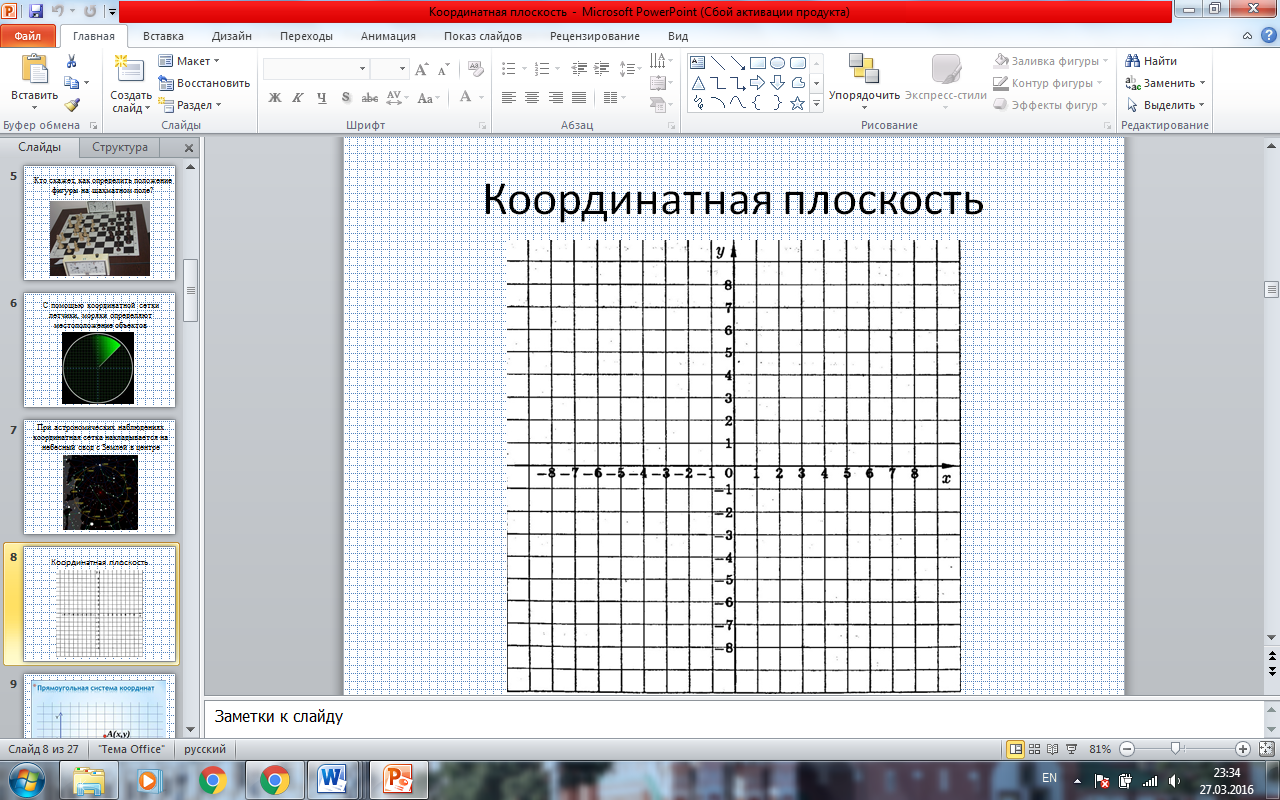
- Здесь нам необходима координатная плоскость. Как же её задать? (предлагают)

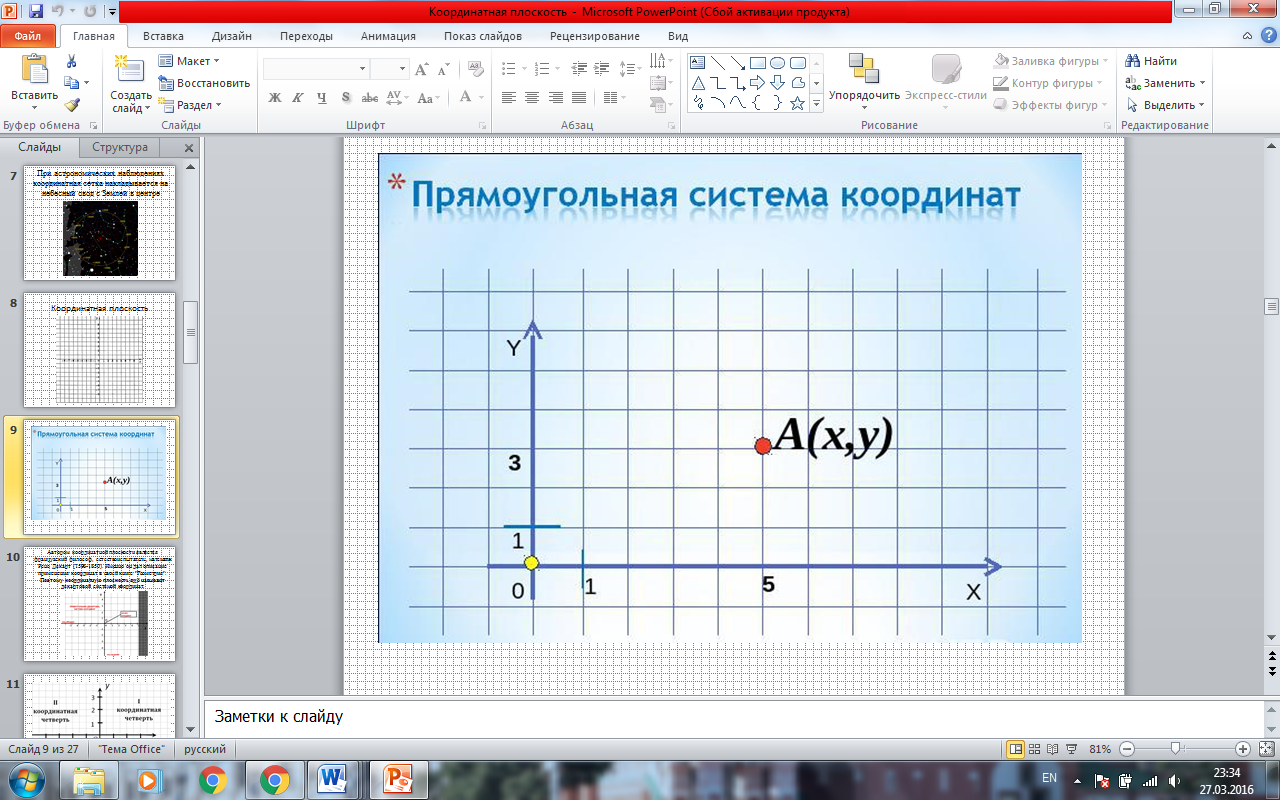
- Прежде всего необходимо построить две перпендикулярные прямые (ПРИЛОЖЕНИЕ. СЛАЙД 9). Точку пересечения этих прямых называют началом отсчёта или началом координат. Две взаимно перпендикулярные прямые с общим началом координат и единичными отрезками образуют систему координат. Координатные прямые - это оси координат, каждая из которых имеет свое название: горизонтальная ось ОХ - ось абсцисс, вертикальная ось ОY - ось ординат.

- Какое направление (положительное или отрицательное) указывают стрелки осей?

- Эту систему называют ещё прямоугольной системой координат. (ПРИЛОЖЕНИЕ. СЛАЙД 10)

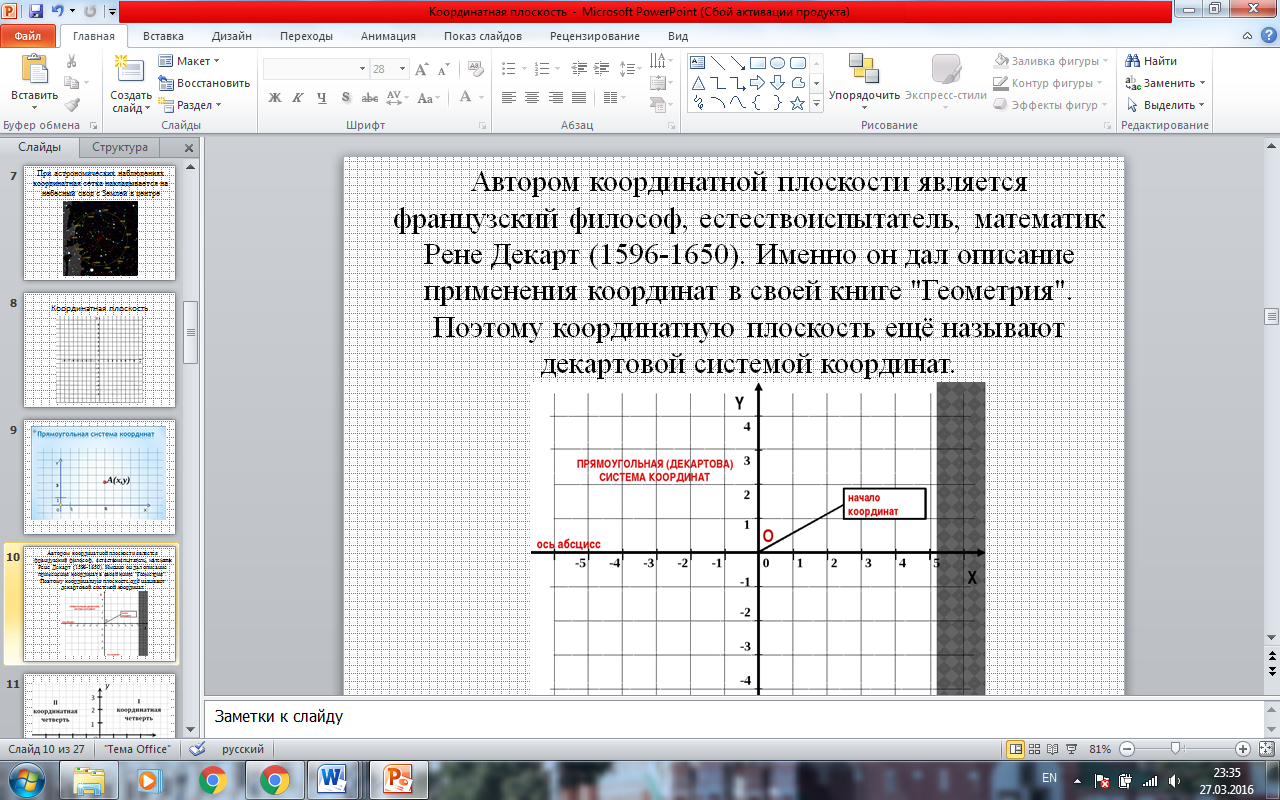
- Автором координатной плоскости является французский философ, естествоиспытатель, математик Рене Декарт (1596-1650). Именно он дал описание применения координат в своей книге "Геометрия". Поэтому координатную плоскость ещё называют декартовой системой координат. (ПРИЛОЖЕНИЕ. СЛАЙД11)

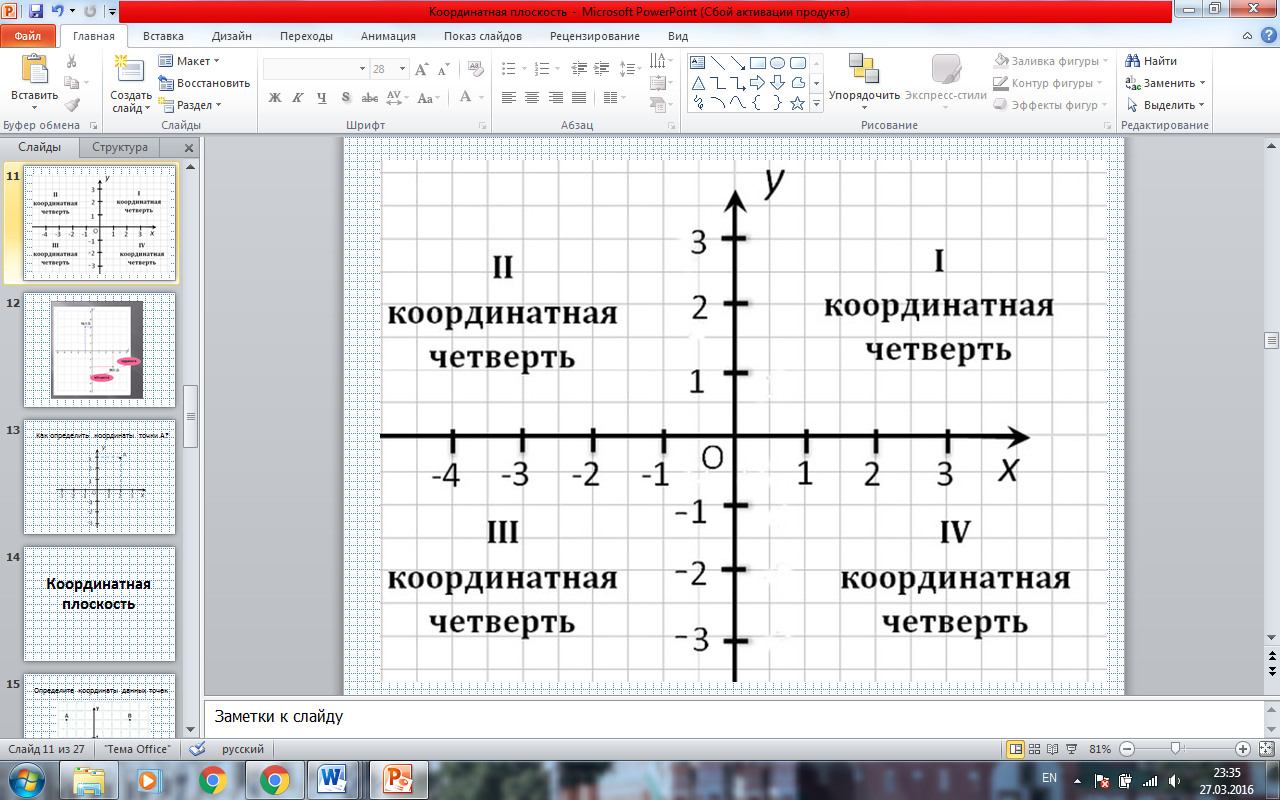
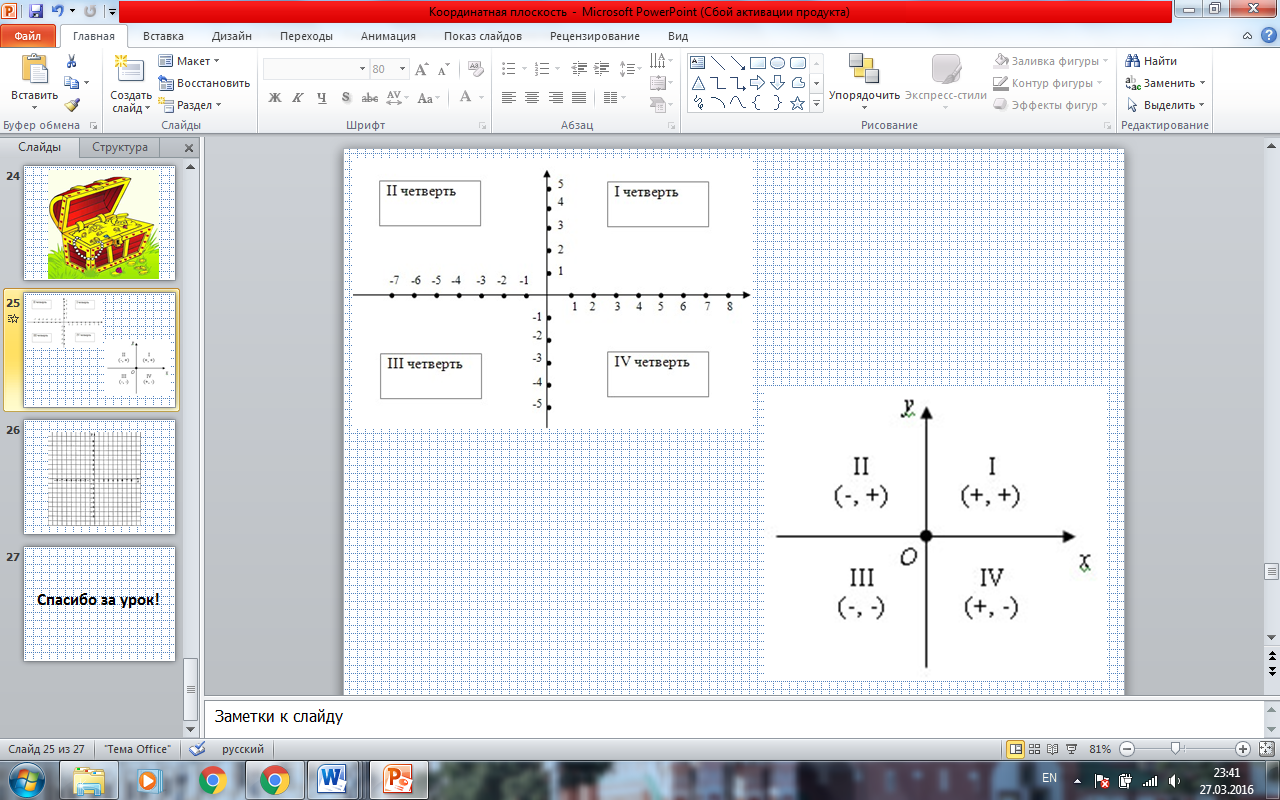
- На сколько частей делят плоскость две взаимно перпендикулярные прямые? (на 4)

- Как, на ваш взгляд, целесообразно назвать одну часть? (четверть) (СЛАЙД 12)

- Первая четверть - четверть, для которой указаны положительные направления обеих осей - чтобы лучше запомнить эту четверть будем считать её самой-самой позитивной. Порядок четвертей идёт против часовой стрелки.

- Сколько чисел на координатной плоскости соответствует каждой точке? (два)

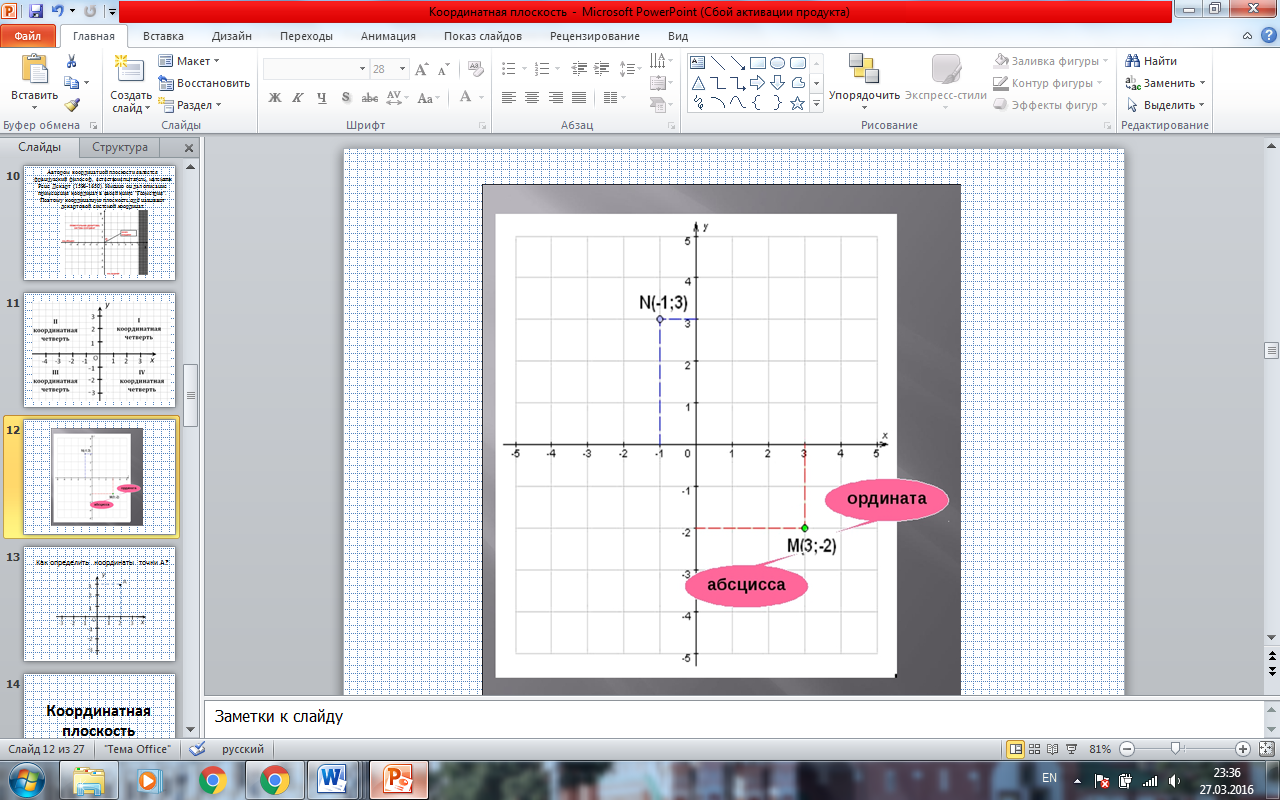
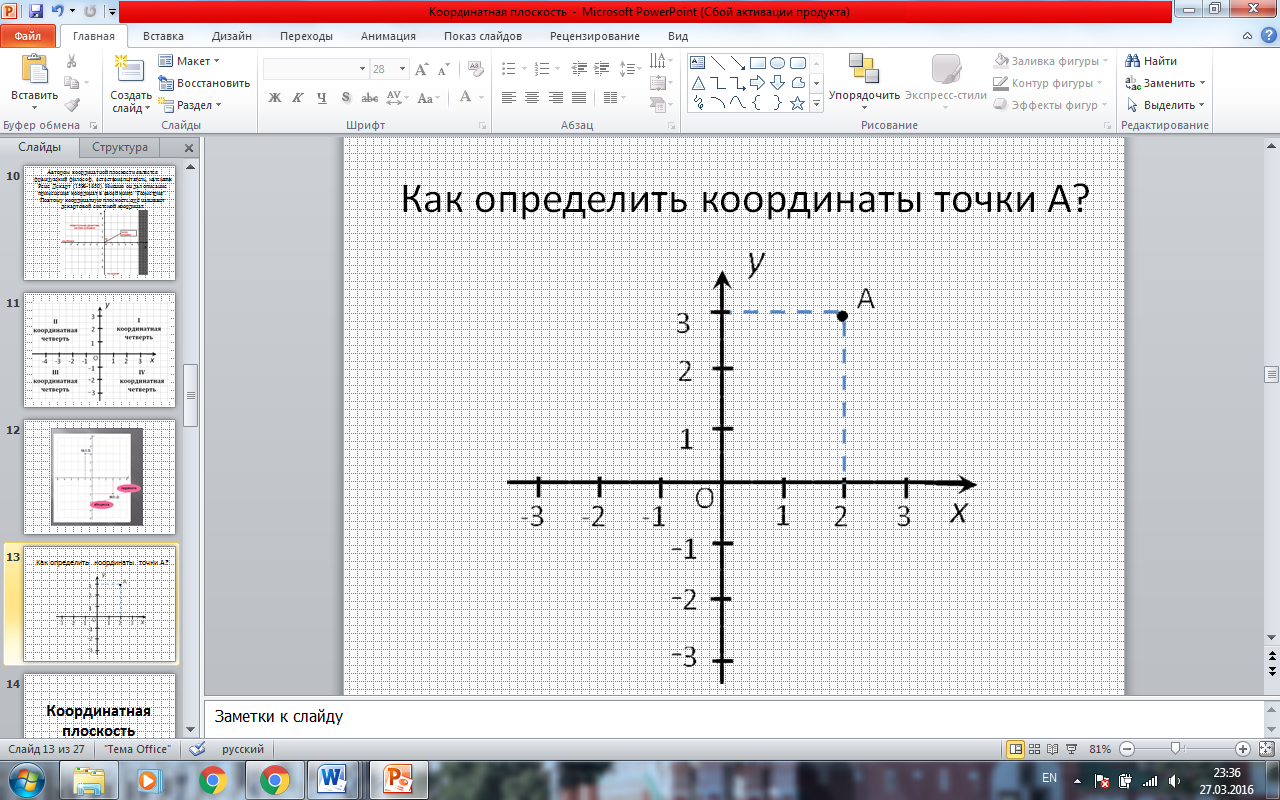
- Каждой точке на плоскости соответствует пара чисел: абсцисса (х) и ордината (у). (ПРИЛОЖЕНИЕ. СЛАЙД13)

- И, наоборот, каждой паре чисел (х; у) соответствует одна точка на плоскости. Координаты точки записывают в скобках через точку с запятой, причем первой всегда записывается координата х, второй - у.

Чтобы не путаться в новых понятиях на первых уроках мы будем использовать вот такие «шпаргалки» (Схема «Система координат»)

IV. Формирование умений и навыков учащихся

- Сегодня на уроке мы должны научиться определять координаты точек, изображенных на плоскости и строить точки по заданным координатам.

- Глядя на рисунок, подумайте и скажите, как определить координаты точки. (ПРИЛОЖЕНИЕ. СЛАЙД 13)

- Откройте тетради, запишите число и тему урока. Какова тема нашего урока? (ПРИЛОЖЕНИЕ.СЛАЙД 14, после озвучивания детьми темы урока)

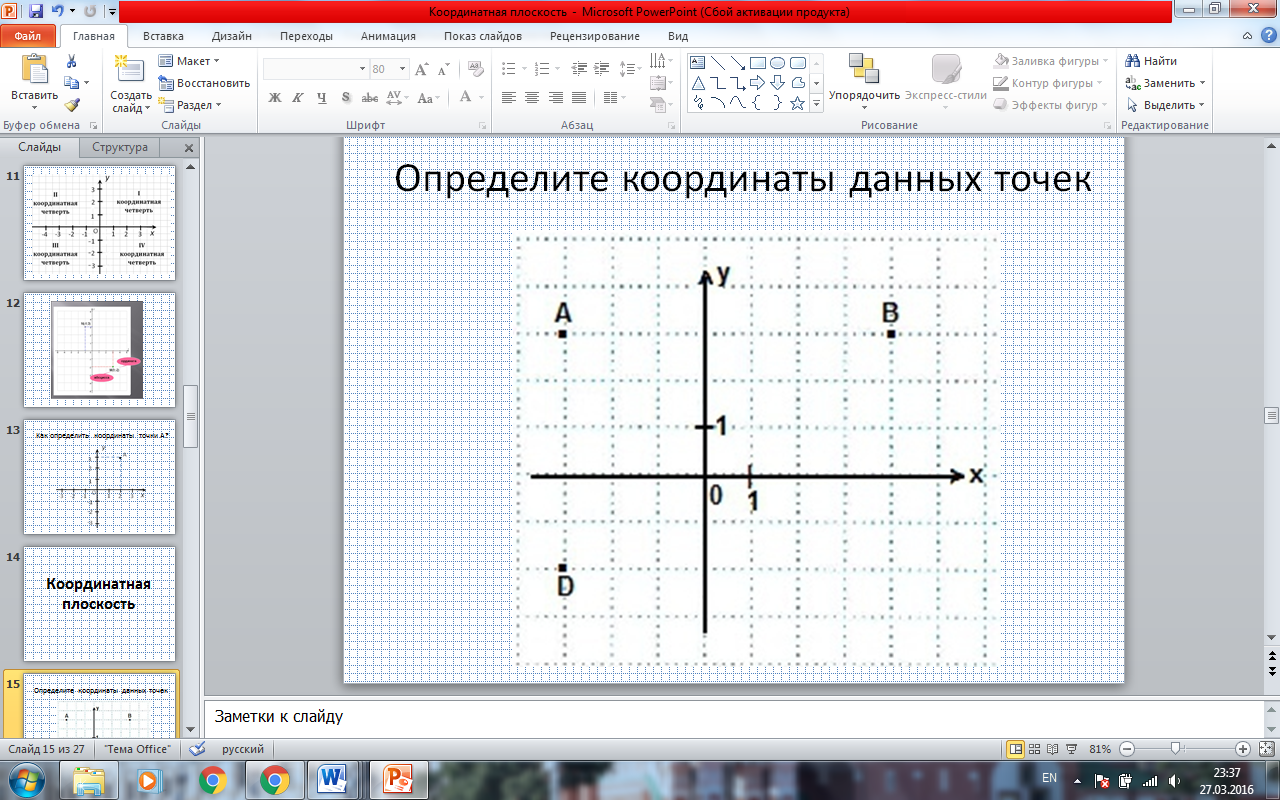
- А теперь мы попробуем определить координаты данных точек. (ПРИЛОЖЕНИЕ. СЛАЙД 15)

- Давайте сначала посмотрим, как были определены координаты точек А и В. (по одному ученику у доски)

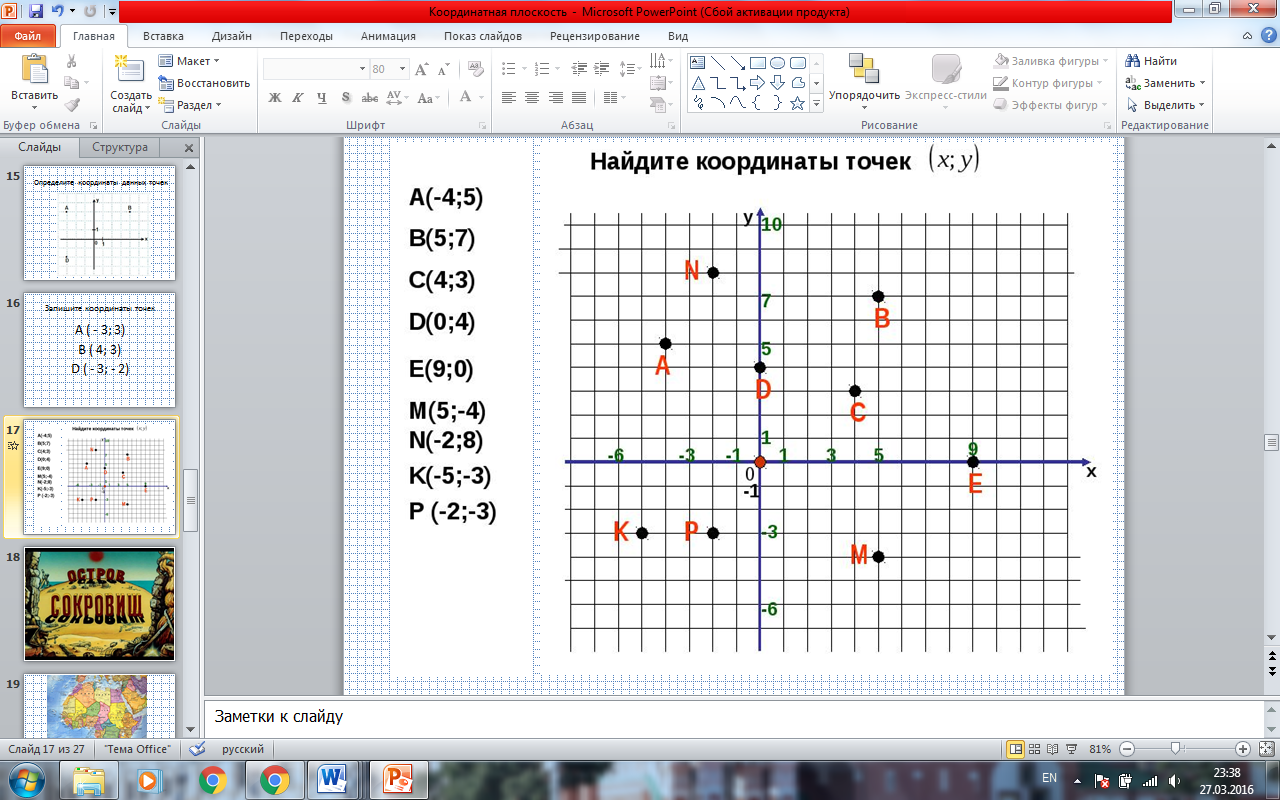
- Запишите координаты точек (по одному ученику озвучивают координаты) (ПРИЛОЖЕНИЕ. СЛАЙД16)

- Что можно сказать о координатах точек, лежащих на оси абсцисс? Ординат?

- А теперь попробуем сами строить в координатной плоскости точки с заданными координатами. (ПРИЛОЖЕНИЕ. СЛАЙД 17, работа детей на интерактивной доске)

- Молодцы, ребята, выполнив эти задания, вы доказали, что готовы к путешествию на "Остров координат" (ПРИЛОЖЕНИЕ. СЛАЙД18)

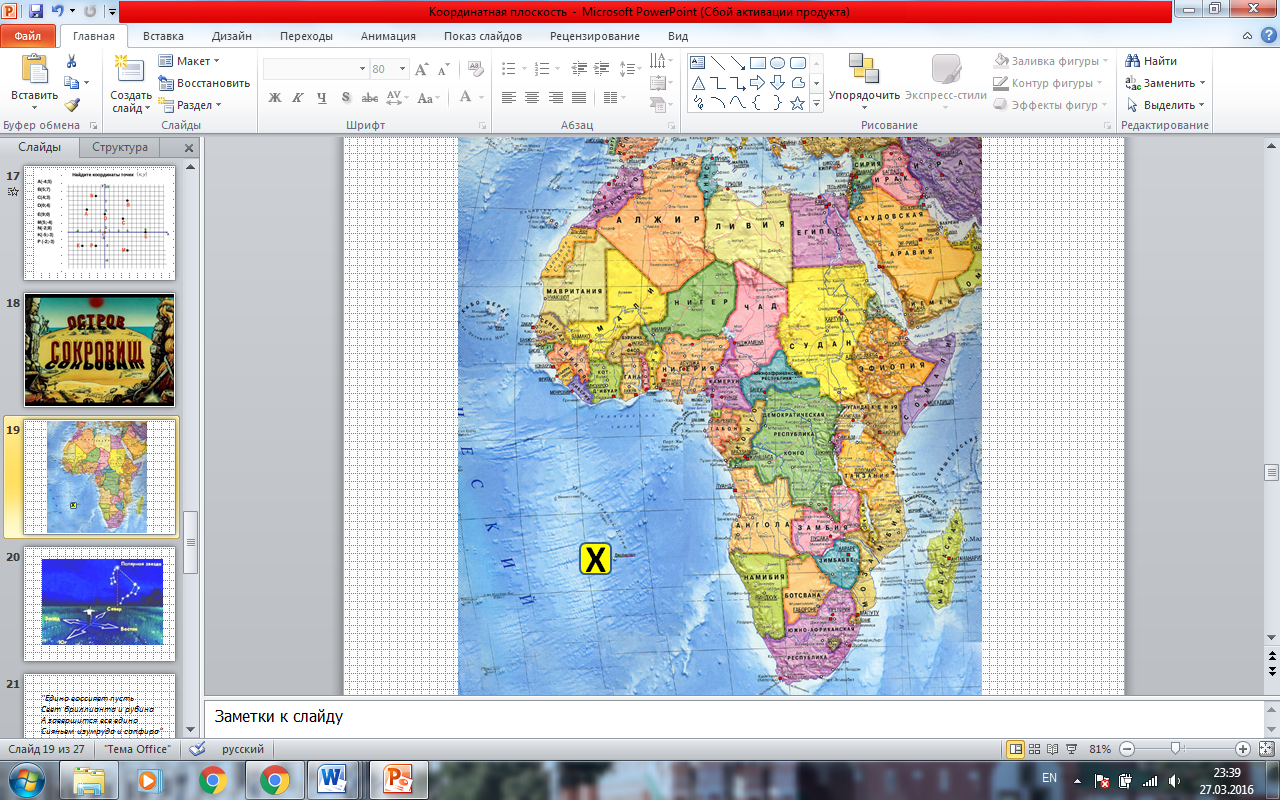
- Давайте посмотрим, где же расположен наш остров (в Атлантическом океане, на юго-западе от Африки) (ПРИЛОЖЕНИЕ. СЛАЙД 19)

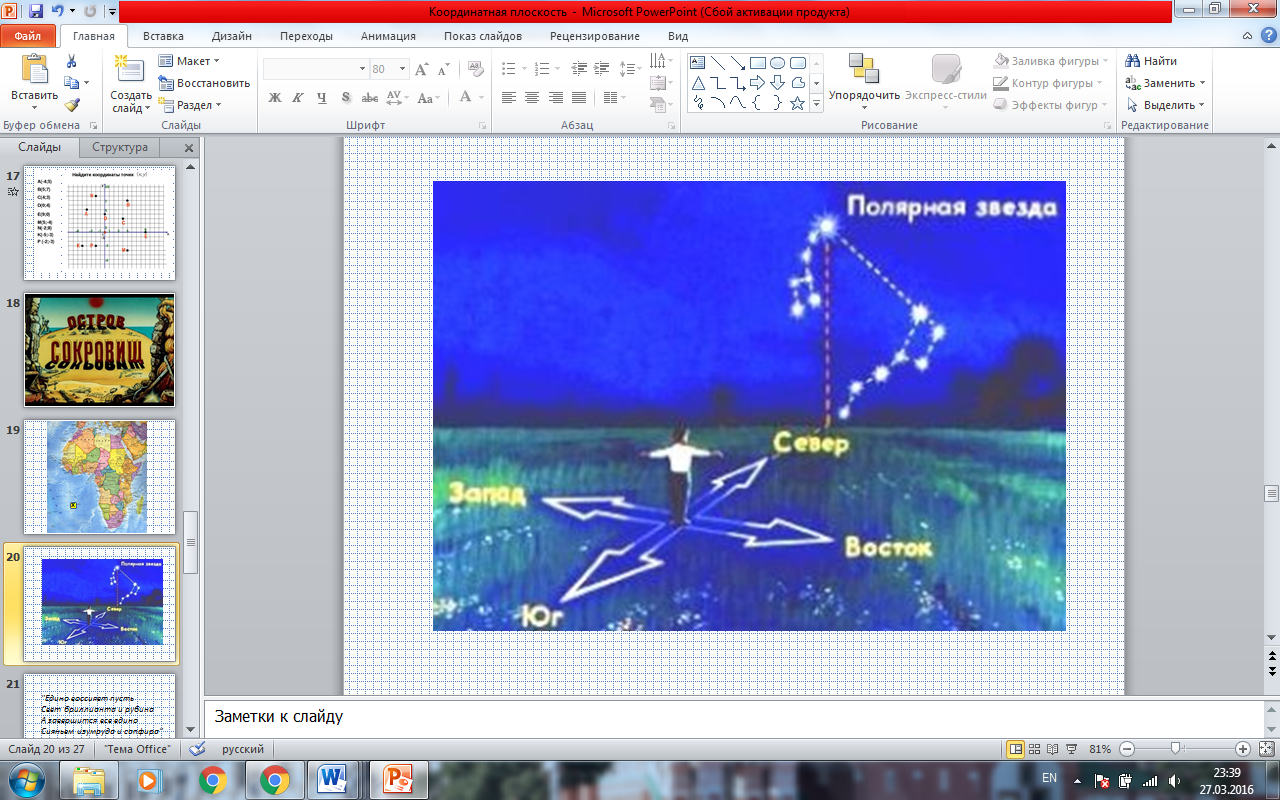
- На острове Сокровищ давным-давно пиратами было закрыто сокровище. Но искать его можно только ночью, причем тогда, когда над островом загорается самая яркая звезда. Попробуем отыскать её на небосводе. (ПРИЛОЖЕНИЕ. СЛАЙД 20)

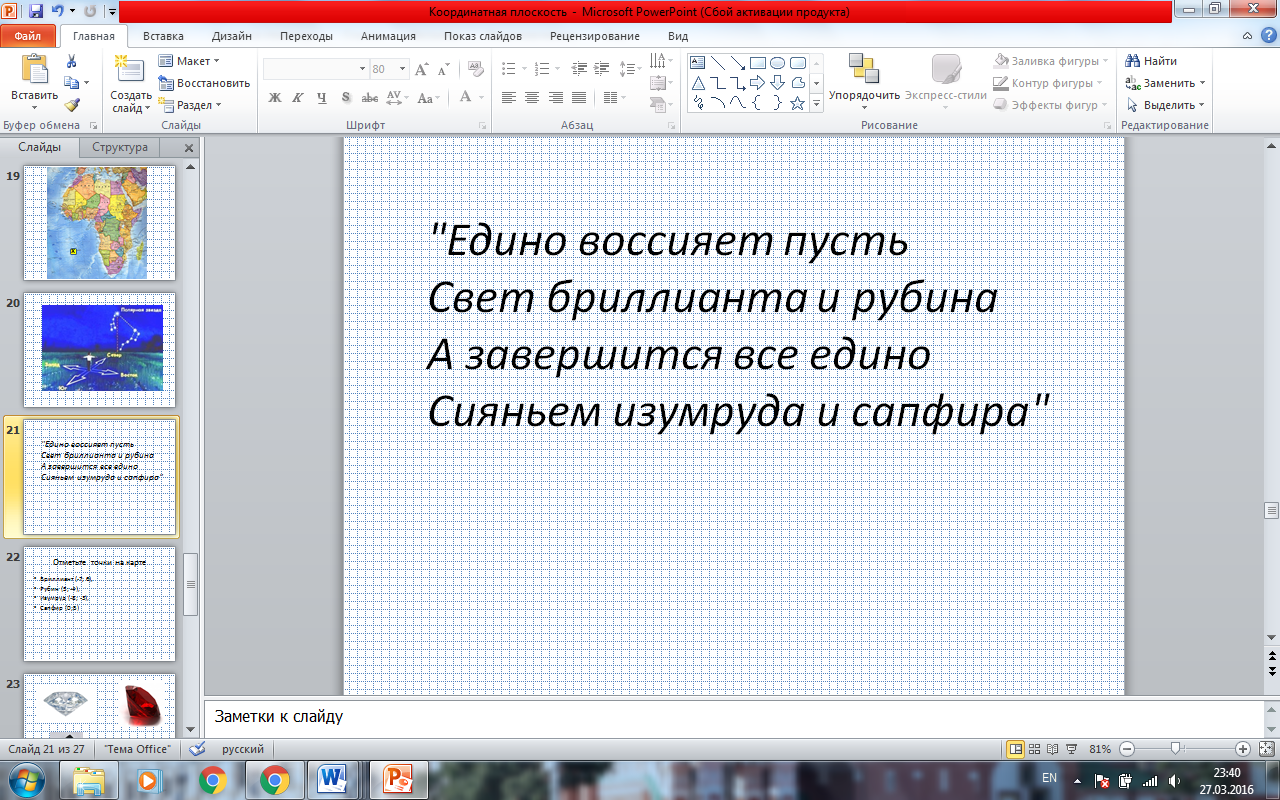
- Клад найдёт лишь тот, кто сможет разгадать и прочитать таинственную карту.

"Едино воссияет пусть

Свет бриллианта и рубина

А завершится все едино

Сияньем изумруда и сапфира" (ПРИЛОЖЕНИЕ. СЛАЙД 21)

Задание: На листочках с готовой координатной плоскостью отметьте точки с заданными координатами, соответствующие названию камней. Соедините точки попарно и найдите точку их пересечения - место клада.

Бриллиант (-7; 6), Рубин (3; -4), Изумруд (-8; -3), Сапфир (0;5) (СЛАЙД 22)

- Пока вы выполняете работу, я озвучу - какими свойствами обладают эти камни. (ПРИЛОЖЕНИЕ. СЛАЙД 23)

- Назовите координаты найденной точки (1;1) Клад найден! Поздравляю! (ПРИЛОЖЕНИЕ. СЛАЙД 24)

V. Подведение итогов

- А теперь подведём итог урока:

1. С каким понятием мы познакомились на уроке? (координатная плоскость)

2. Как по-другому можно назвать координатную плоскость? (система координат, прямоугольная система координат, декартова система координат)

3. Как называются прямые, образующие систему координат? (ось абсцисс ОХ, ось ординат ОУ)

4. Каково их взаимное расположение? (перпендикулярны)

5. Как называют точку их пересечения? (началом координат)

6. Чем задаётся положение точки на плоскости? (абсциссой, ординатой)

7. Как называют первое число? Второе число?

8. У каких точек на координатной плоскости абсцисса равна нулю? (лежащих на оси ОУ)

9. У каких точек равна нулю ордината? (лежащих на оси ОХ)

10. Какая точка имеет координаты (0;0)?

11. Какой знак (+ или -) имеет абсцисса точки, расположенной в 1 координатной четверти? А ордината?

12. Определите знаки координат точки, расположенной во второй четверти, в третьей, в четвертой. (ПРИЛОЖЕНИЕ. СЛАЙД 25, показать после ответа ребят)

VI. Рефлексивно-оценочная часть

- Наш урок подходит к концу, и мы должны подвести итоги, оценить, чего мы достигли. Для этого я предлагаю вам подойти к нашей системе координат и отметить ту точку, в которой вы сейчас находитесь: ось ординат отвечает за интерес, а ось абсцисс - за то, насколько понятен вам материал (дети выходят к доске и отмечают точки на интерактивной доске) (ПРИЛОЖЕНИЕ. СЛАЙД 26)

ПРИЛОЖЕНИЯ