- Учителю
- Конспект урока алгебры в 11 классе по теме Решение нестандартных показательных уравнений
Конспект урока алгебры в 11 классе по теме Решение нестандартных показательных уравнений
государственное бюджетное общеобразовательное учреждение
Самарской области лицей города Сызрани
городского округа Сызрань Самарской области
Открытый урок по алгебре и началам анализа в 11 классе:
«Решение нестандартных показательных уравнений»
(комбинированный урок)
Форма урока: урок-практикум
Уровень: школьный
Составила: учитель математики
Гусева Наталья Владимировна
г. Сызрань
2014-2015 учебный год
Открытый урок по теме:
«Решение нестандартных показательных уравнений».
Цели:
Образовательные:
-
систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения показательных уравнений;
-
сформировать умения решать нестандартные показательные уравнения;
-
способствовать развитию навыков самостоятельного применения знаний при решении показательных уравнений, в том числе нестандартными способами.
Развивающие:
-
формировать познавательную мотивацию учащихся в учебный процесс;
-
формировать эмоциональную включенность учащихся в учебный процесс;
-
формировать развитие познавательного интереса;
-
формировать развитие у учащихся самостоятельности.
Воспитательные:
-
умственное воспитание: формирование логического, абстрактного, системного мышления;
-
воспитание сознательной дисциплины и норм поведения;
-
воспитание ответственности, умения принимать самостоятельные решения;
-
воспитание интереса к истории математики как науки.
Оборудование: интерактивная доска, слайдовая презентация.
План урока:
I. Проверка домашнего задания.
II. Повторение теоретического материала.
III. Изучение нового материала. Решение нестандартных показательных уравнений.
IV. Самостоятельная работа по выбору.
V. Подведение итогов урока.
VI. Задание на дом.
Ход урока
I. Проверка домашнего задания.
II. Повторение теоретического материала.
Фронтальный опрос учащихся.
-
Какая функция называется показательной?
-
Какими свойствами обладает показательная функция?
-
Какова её область определения?
-
Какова область изменения?
-
Какова показательная функция по монотонности?
-
Возрастает или убывает функция:
а) y=![]() ;
б) y=
;
б) y=![]() ;
в) y=
;
в) y=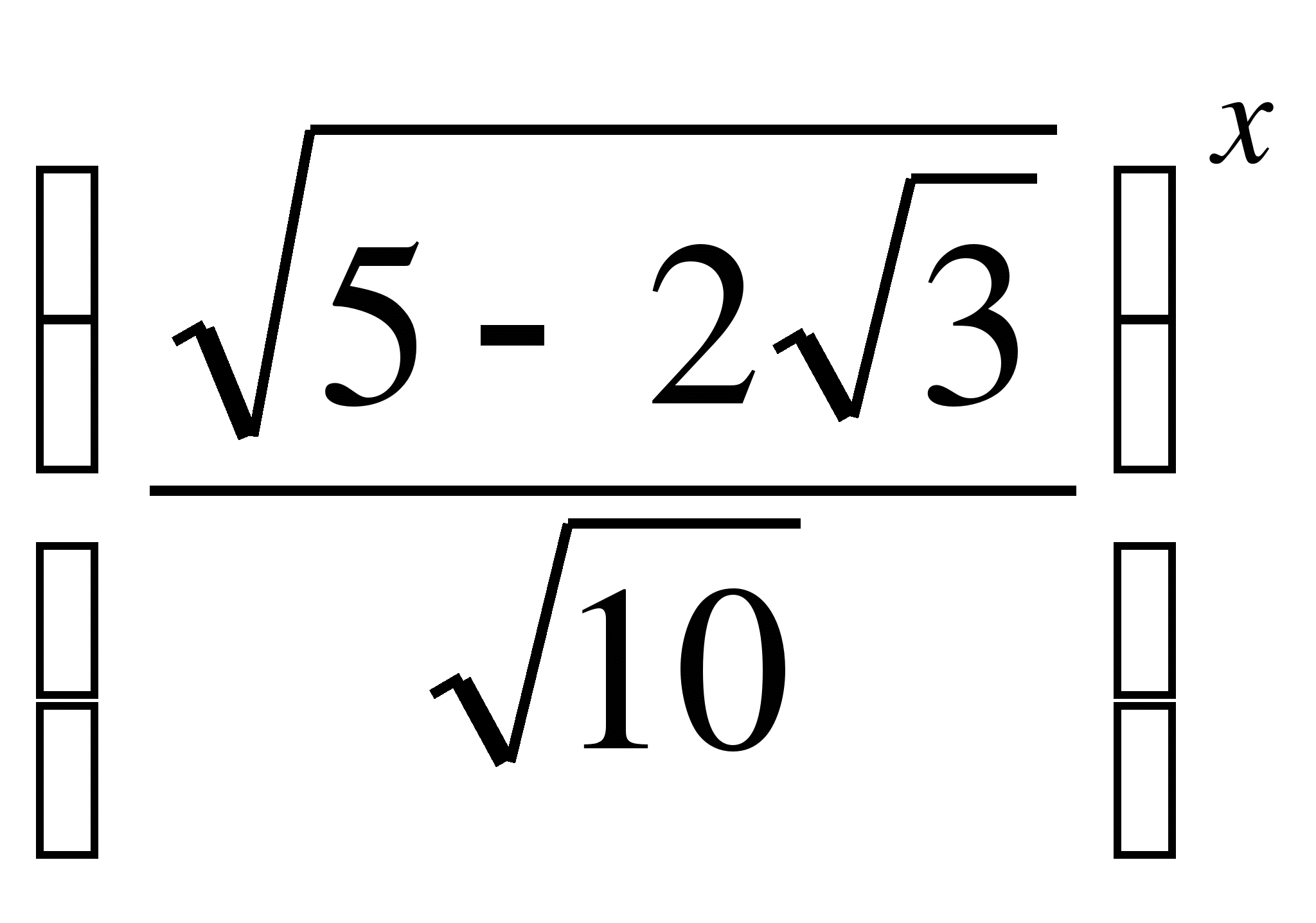 ;
г) y=
;
г) y=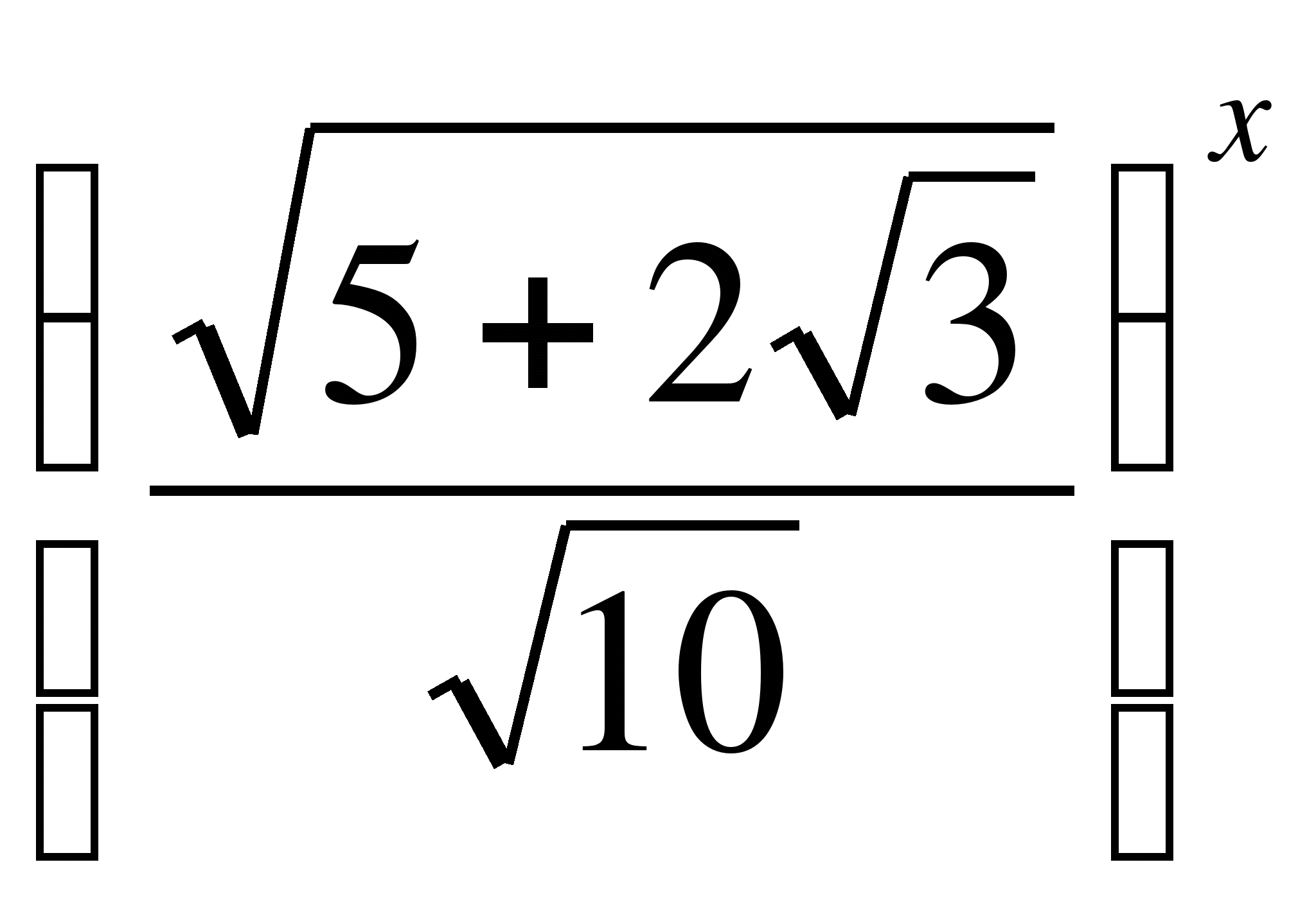 ?
?
-
Сформулируйте теорему о корне.
- Повторим методы решения простейших показательных уравнений на конкретных примерах. Как будете решать уравнения? (слайдовая презентация)
1) ![]()
2) ![]()
3) ![]()
4) 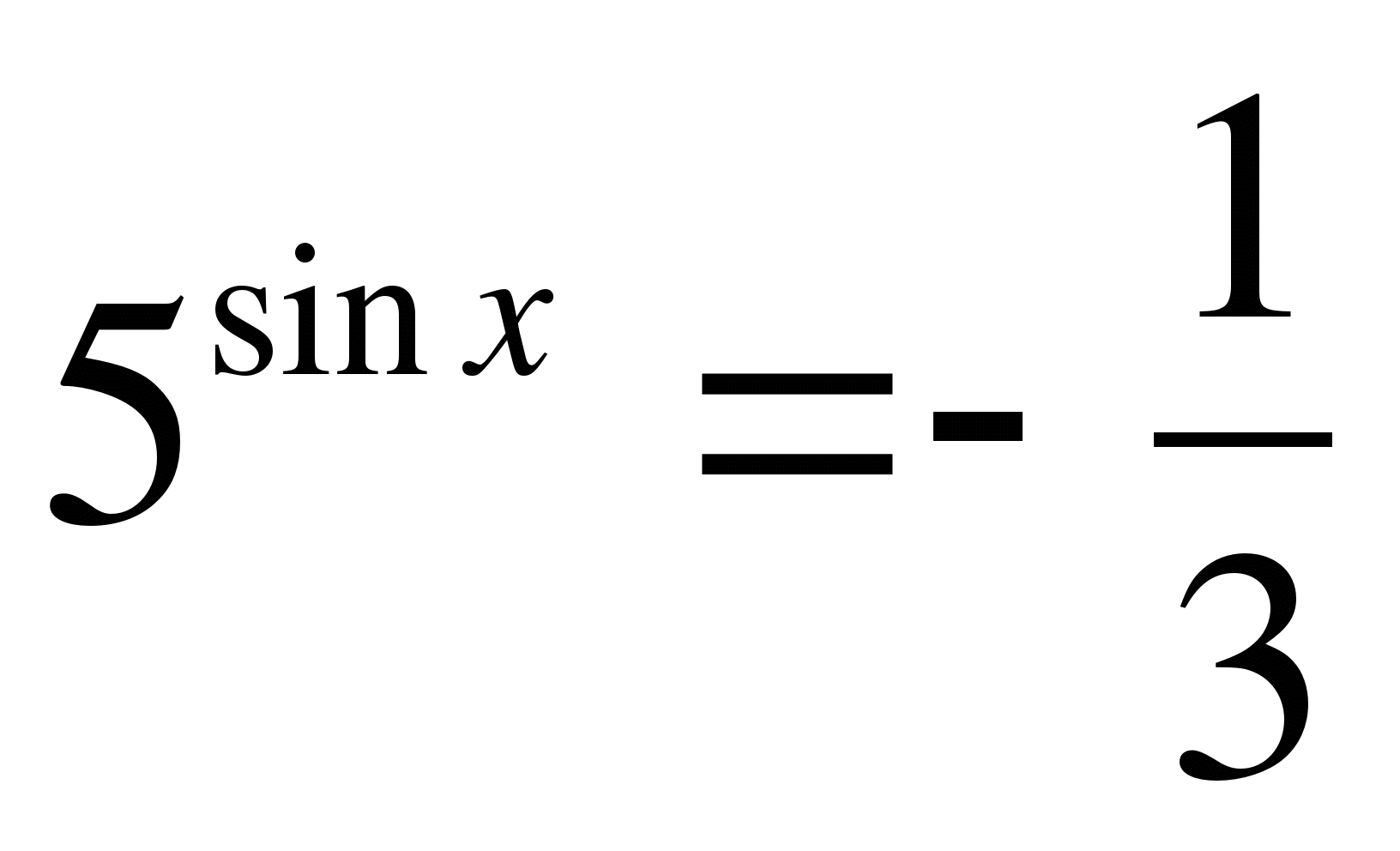
5) ![]()
III. Изучение нового материала. Решение нестандартных показательных уравнений.
Решить уравнения:
1) ![]() (Учитель на доске дает образец решения уравнения.)
(Учитель на доске дает образец решения уравнения.)
Решение.
Подбором определяем, что x=2 - корень данного уравнения.
![]()
Докажем, что других корней у уравнения нет.
![]() ,
так как
,
так как ![]() , то и
, то и 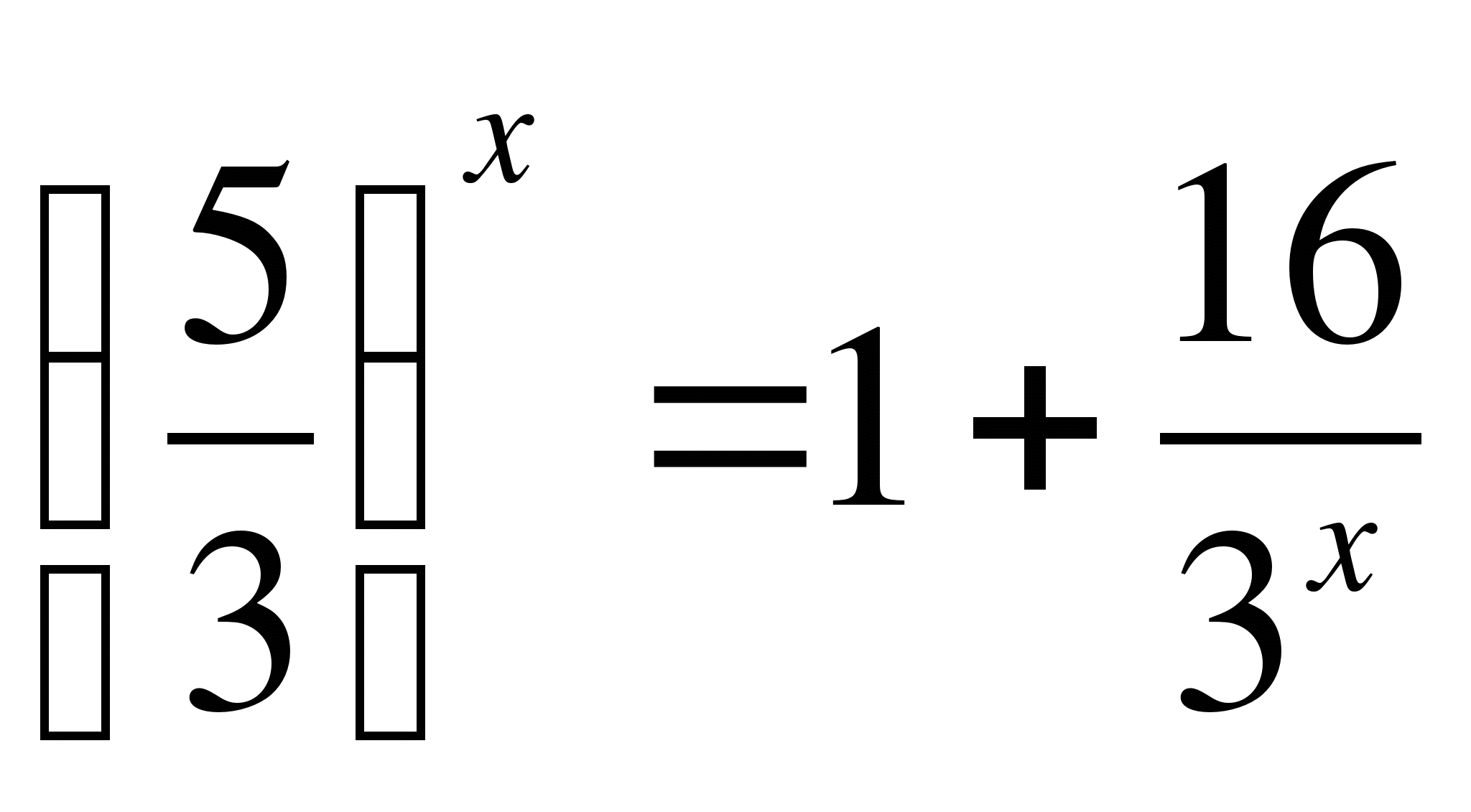 .
.
Функция 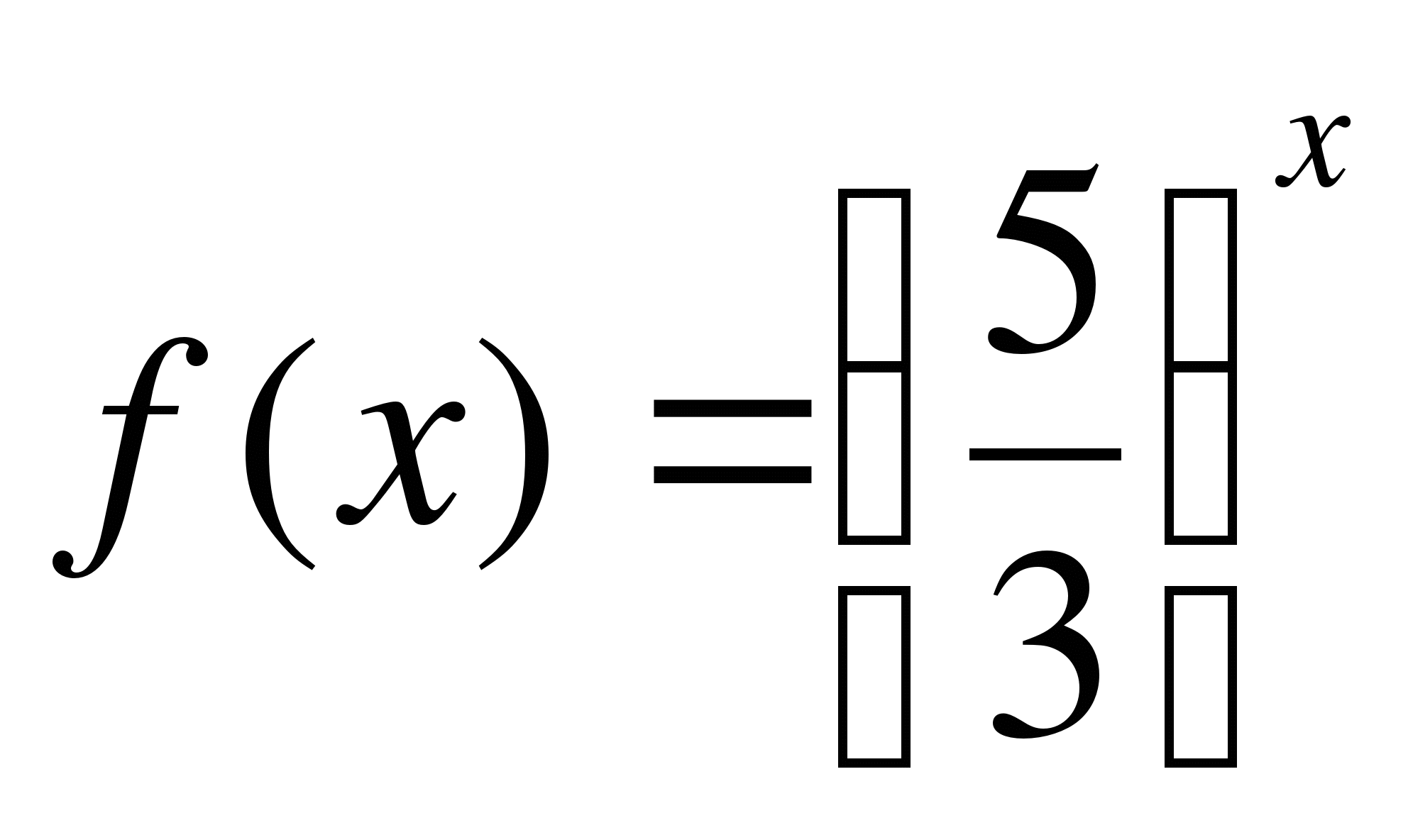 - возрастающая на R, а функция
- возрастающая на R, а функция 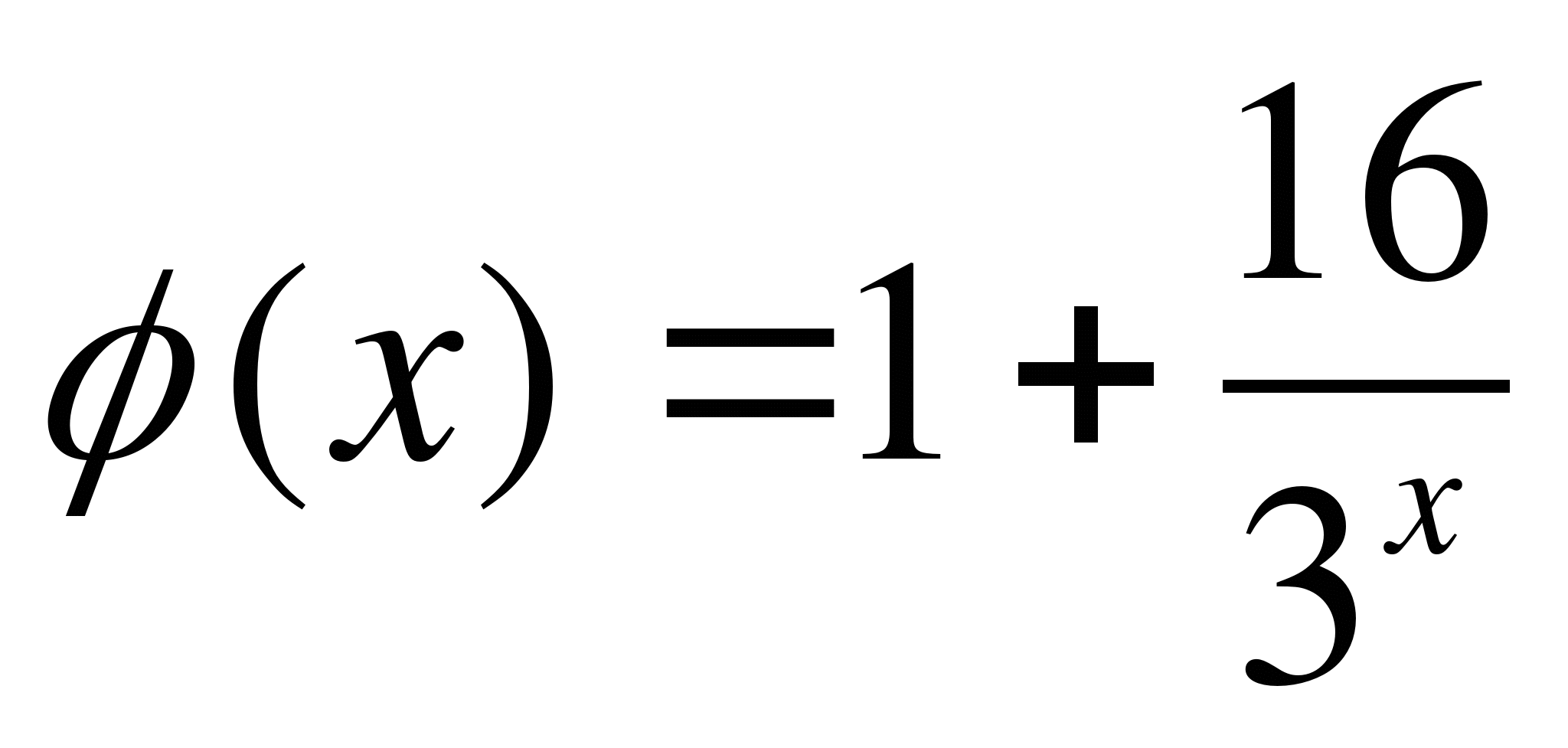 - убывающая на R.
- убывающая на R.
Значит, уравнение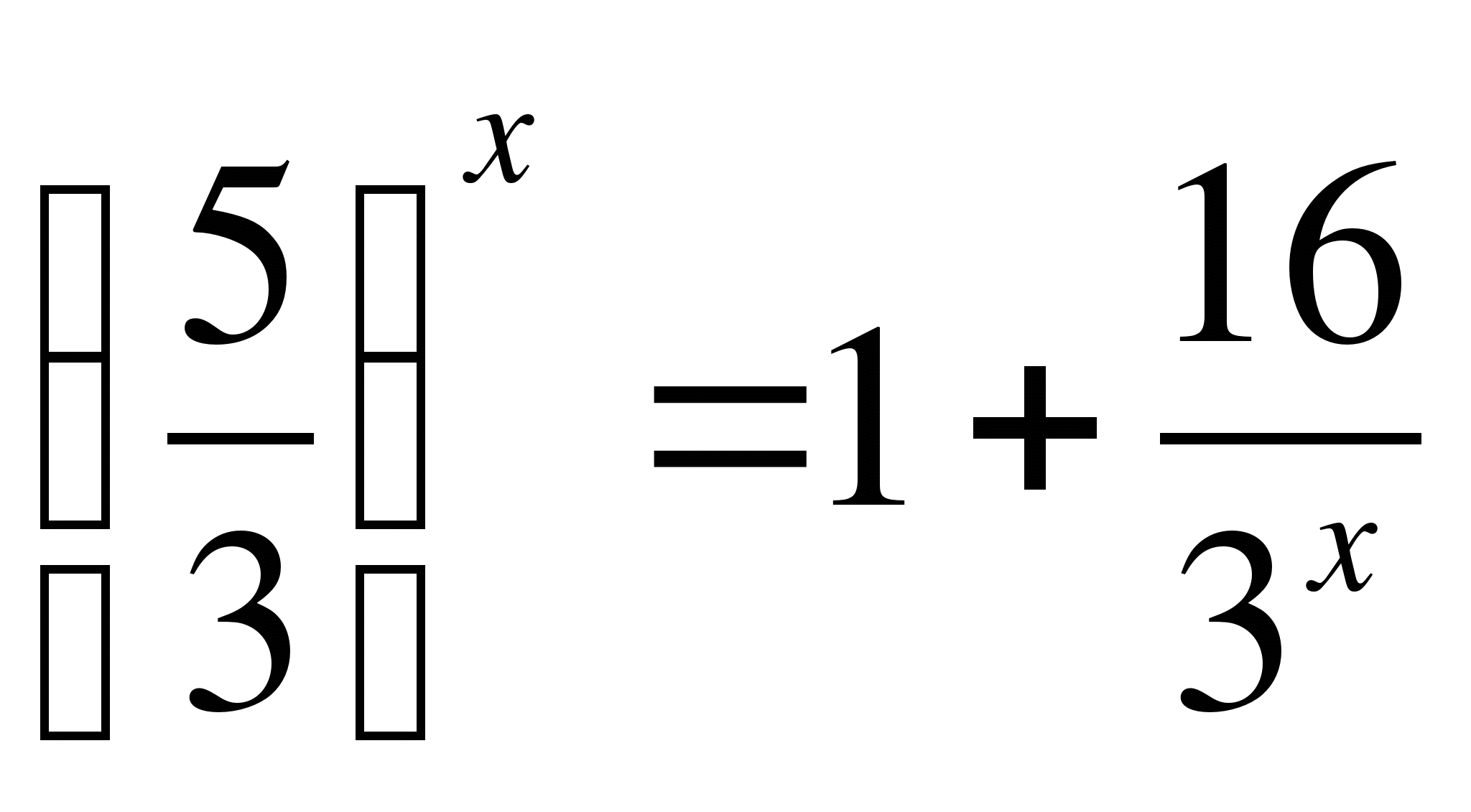 имеет единственный корень. Поэтому корней у данного уравнения,
кроме
имеет единственный корень. Поэтому корней у данного уравнения,
кроме ![]() , нет.
, нет.
Ответ: 2.
2) ![]() (Учитель делает только первый переход к равносильному уравнению, а
затем кто-то из учеников решает на доске, комментируя решение.)
(Учитель делает только первый переход к равносильному уравнению, а
затем кто-то из учеников решает на доске, комментируя решение.)
Решение:
1-ый способ.
![]()
![]()
![]() ,
,
так как![]() ,
то
,
то ![]()
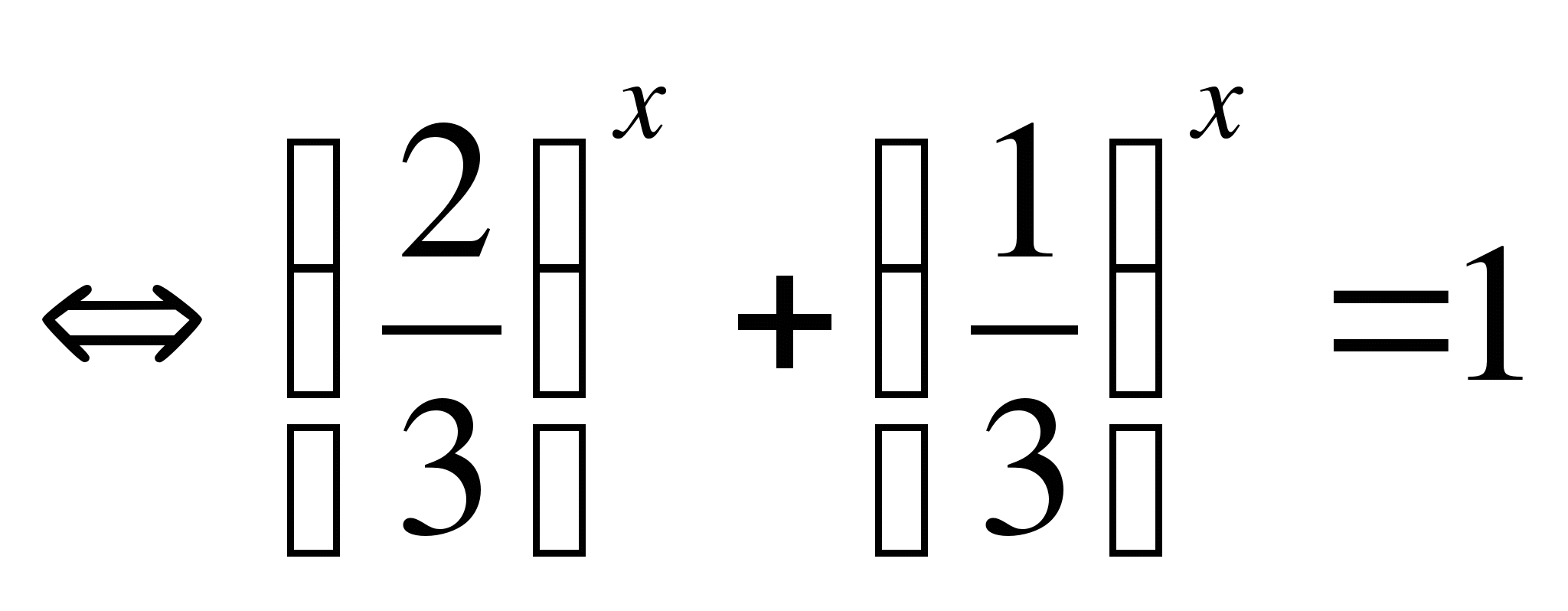
В левой части уравнения убывающая функция (как сумма двух
убывающих функций, поэтому, если уравнение имеет корень, то он
единственный). Очевидно, что ![]() , так как
, так как 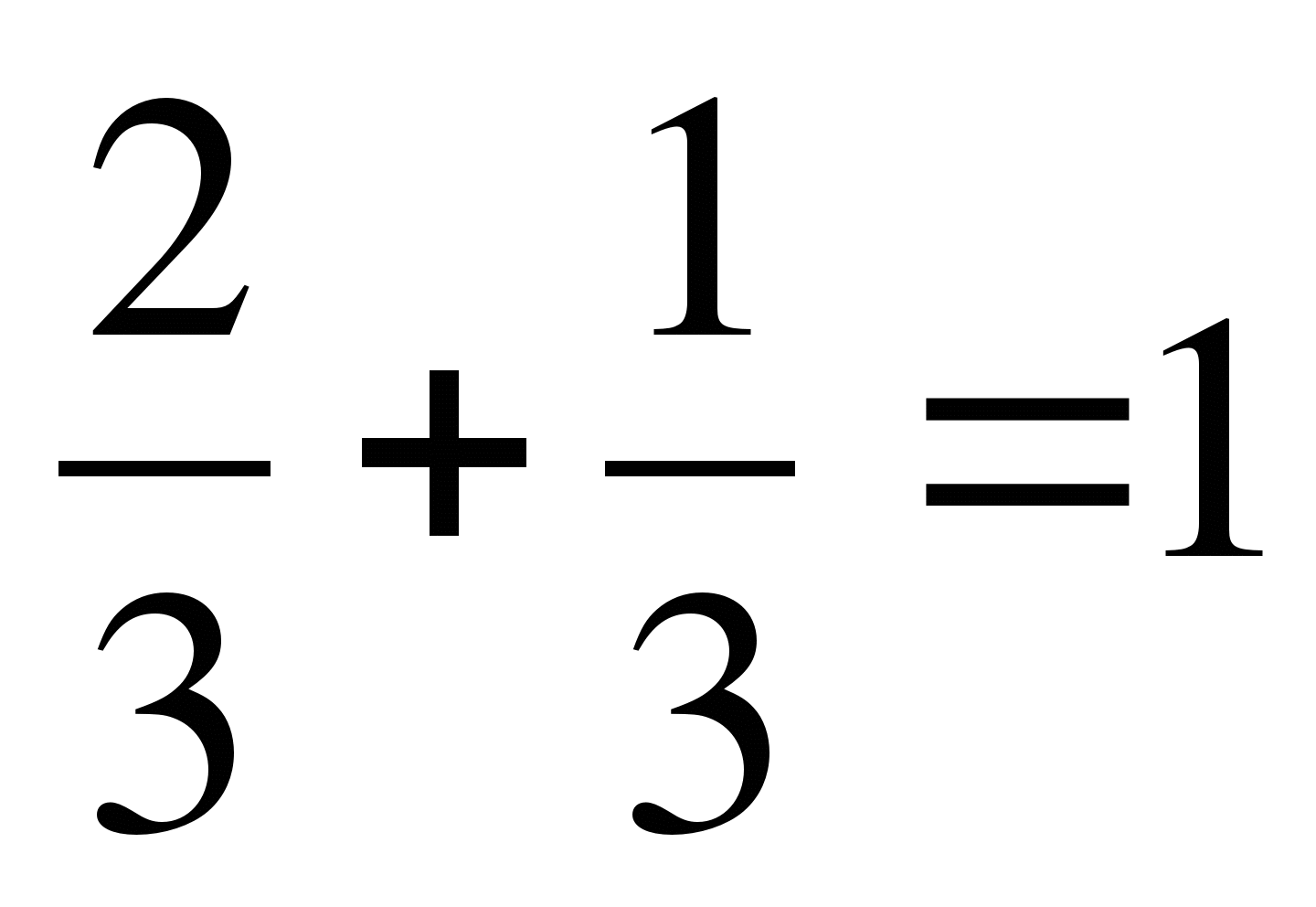
Ответ: 1.
2-й способ.
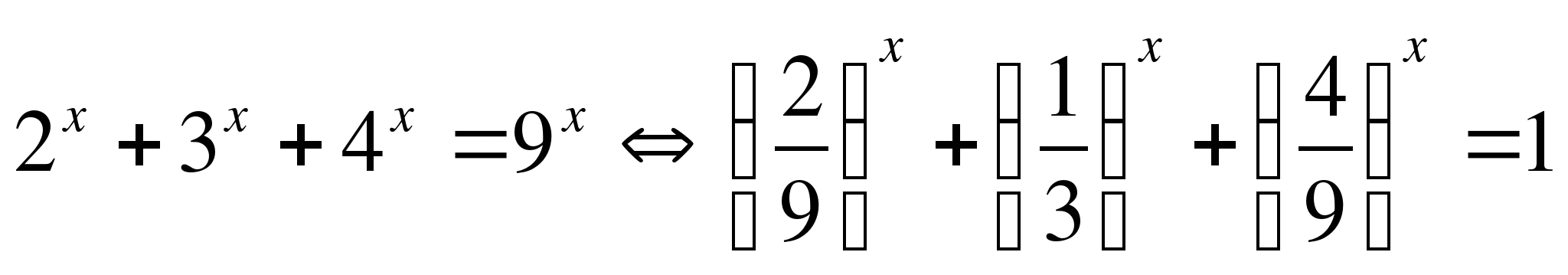 ,
так как
,
так как ![]() .
.
В левой части уравнения убывающая функция (как сумма трех убывающих показательных функций). Тогда по теореме о корне - уравнение имеет единственный корень, а поэтому единственный корень имеет и равносильное ему данное уравнение.
![]() .
.
Нетрудно видеть, что ![]() - корень
- корень ![]()
Ответ: 1.
3) 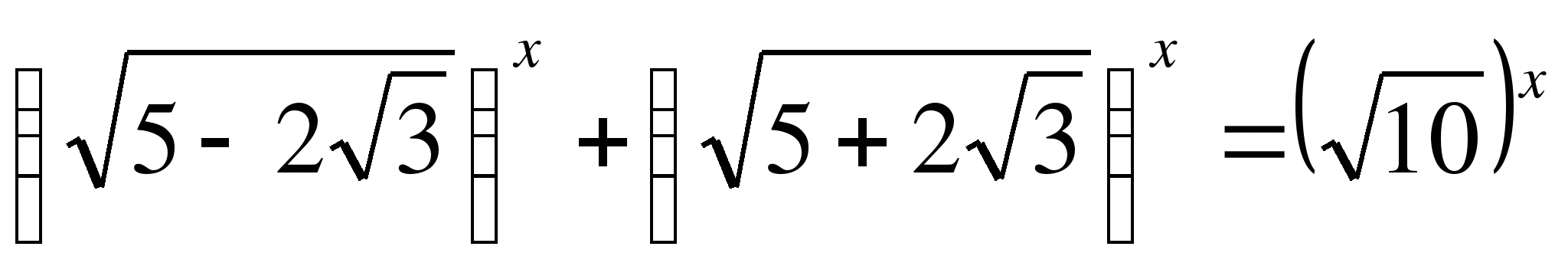
Решение: (Один из учащихся решает на доске)
![]() ,
разделим обе части уравнения на
,
разделим обе части уравнения на ![]() , тогда
, тогда
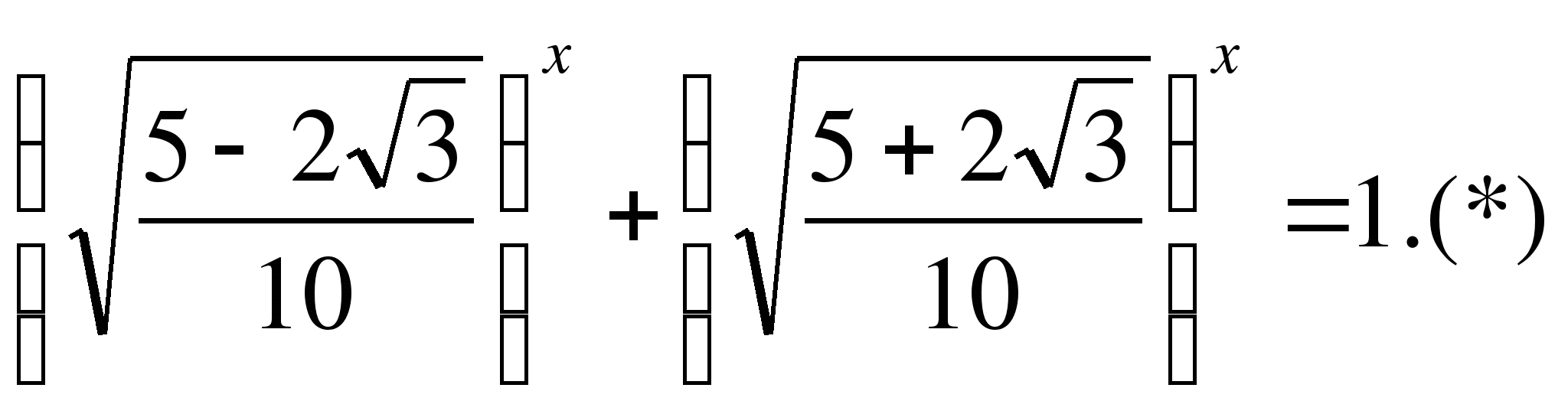
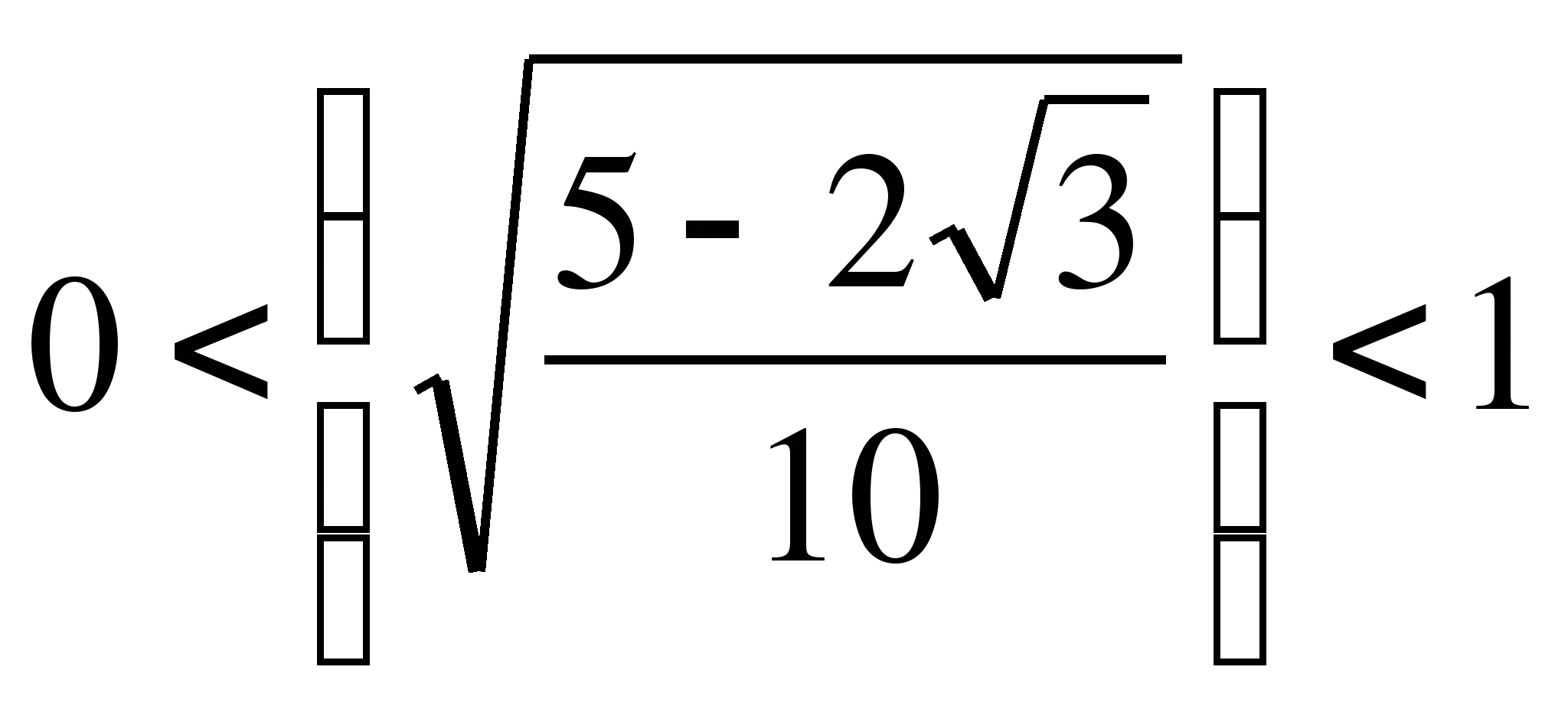 и
и
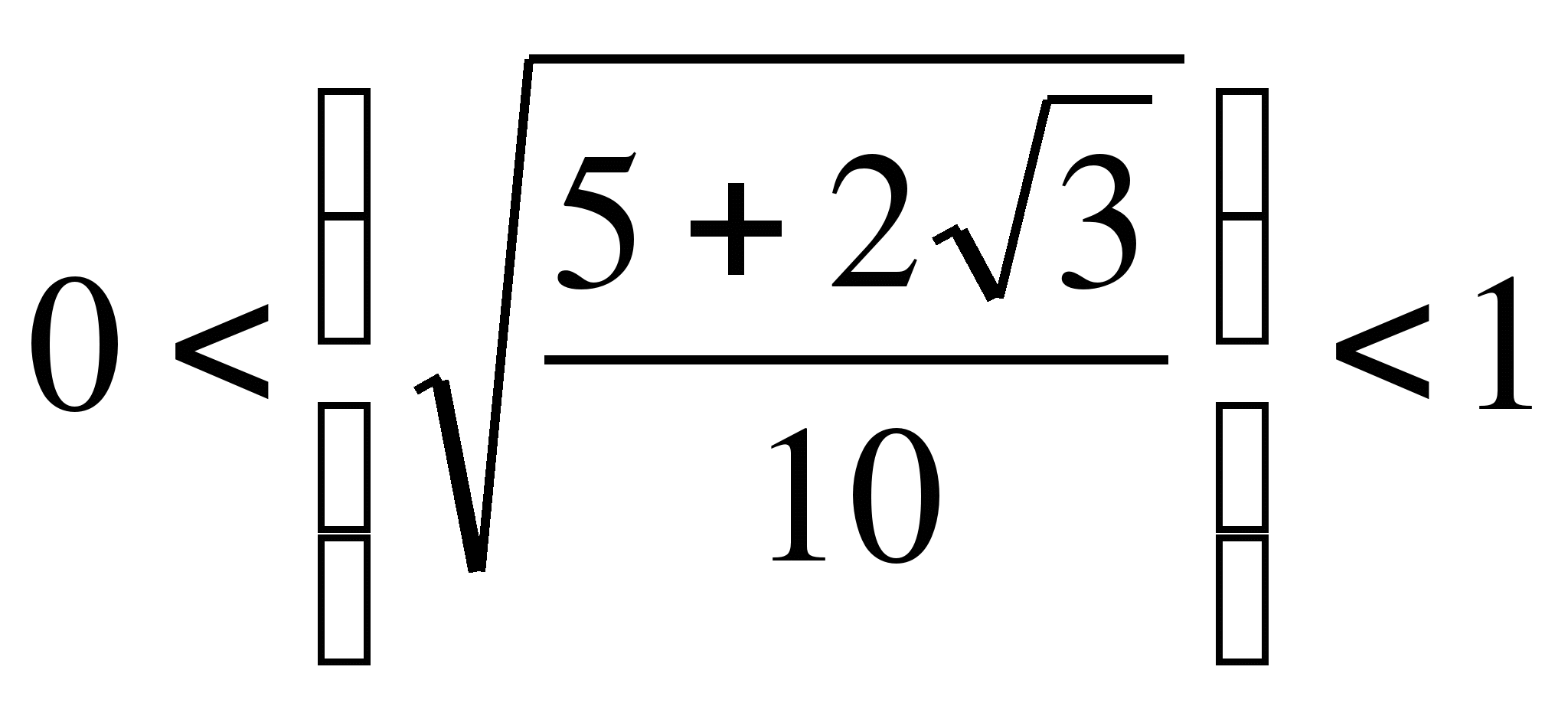
В левой части уравнения (*) - сумма двух убывающих функций есть функция убывающая. А поэтому, если уравнение (*) имеет корень, то он единственный.
![]()
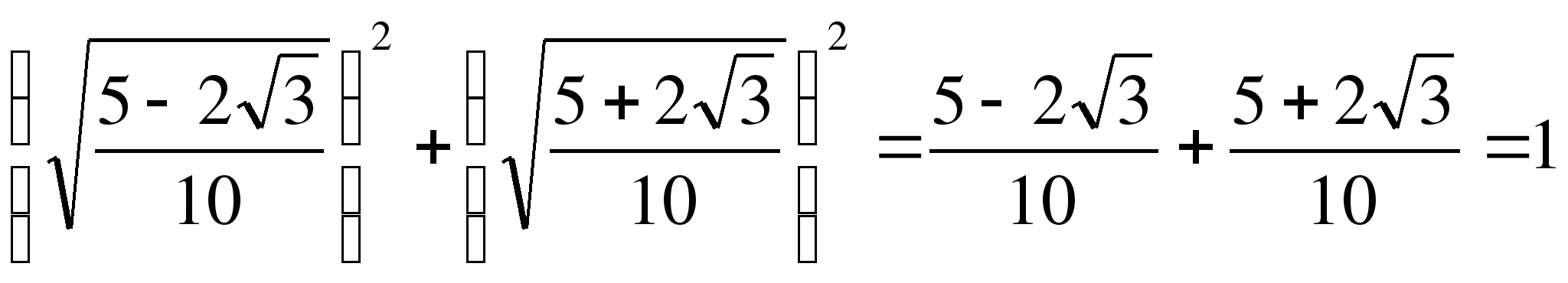
Ответ: 2.
4) ![]()
Решение:
Найдем О.Д.З. х: ![]() .
.
![]()
Произведение двух множителей равно нулю тогда и только тогда, когда один из них равен нулю, а другой при этом не теряет смысла.
![]() или
или
![]()
![]() Пусть
Пусть
![]() , тогда
, тогда
![]()
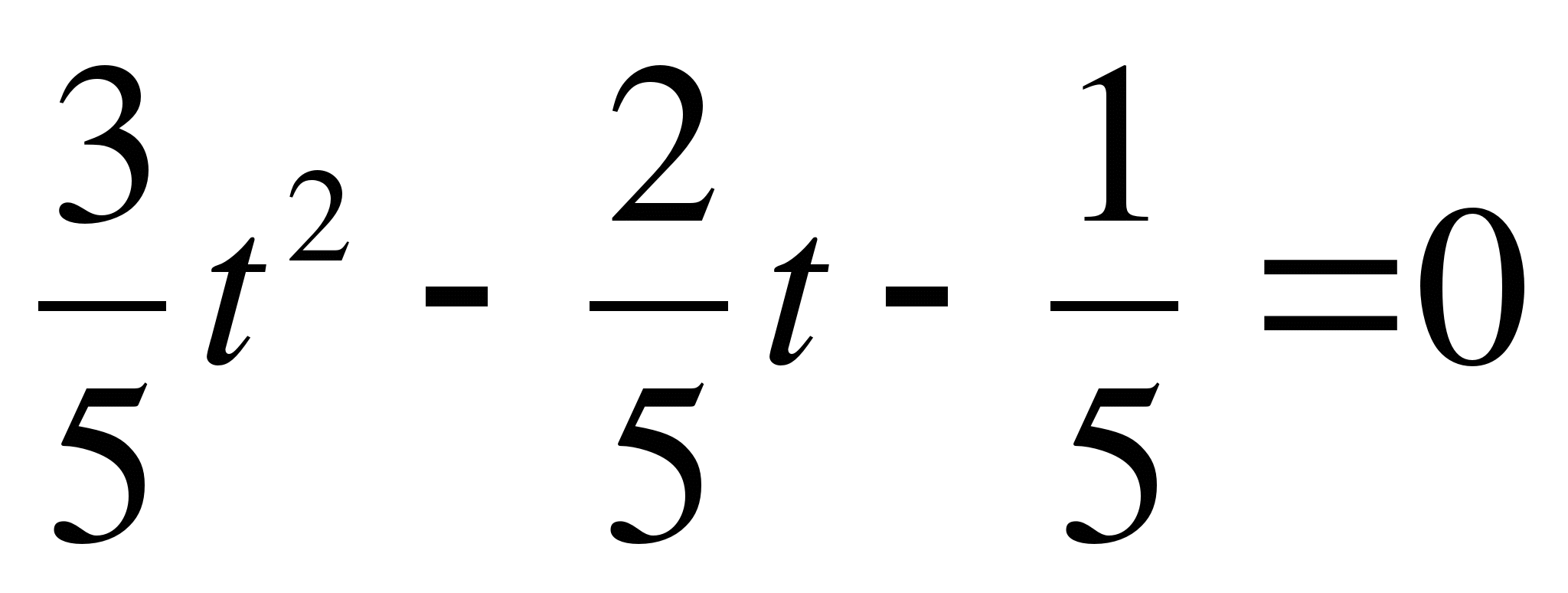
![]()
![]()
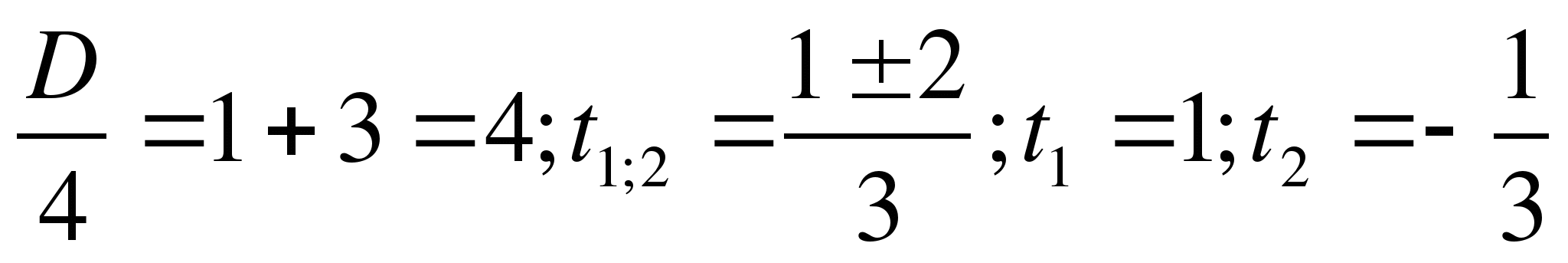
![]() или
или 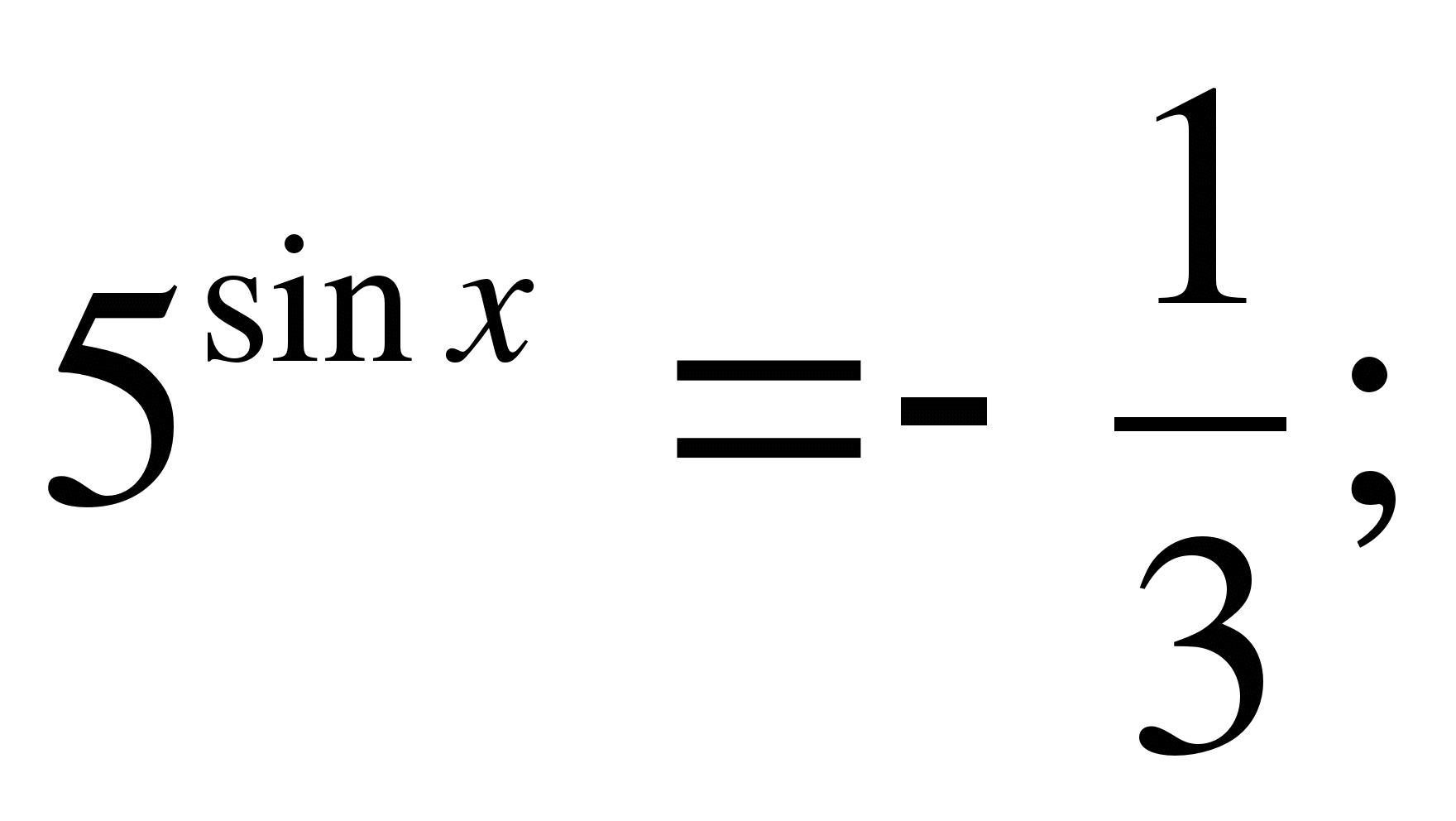
![]() Пустое множество
Пустое множество
![]() ,
,
но ![]() (О.Д.З.), т.е.
(О.Д.З.), т.е.
![]() (это
третий корень
(это
третий корень
данного уравнения). Ответ: 1; 5; ![]() .
.
5) ![]()
Решение:
Обозначим ![]() ,
, ![]() и получим квадратное относительно y уравнение.
и получим квадратное относительно y уравнение.
![]()
![]()
![]()
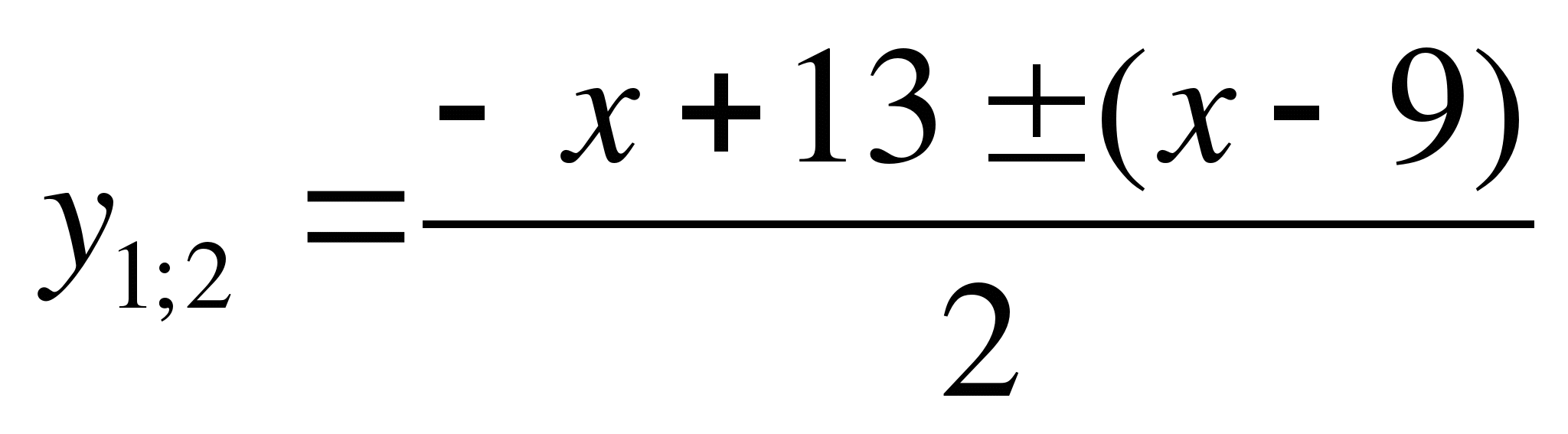 ;
;
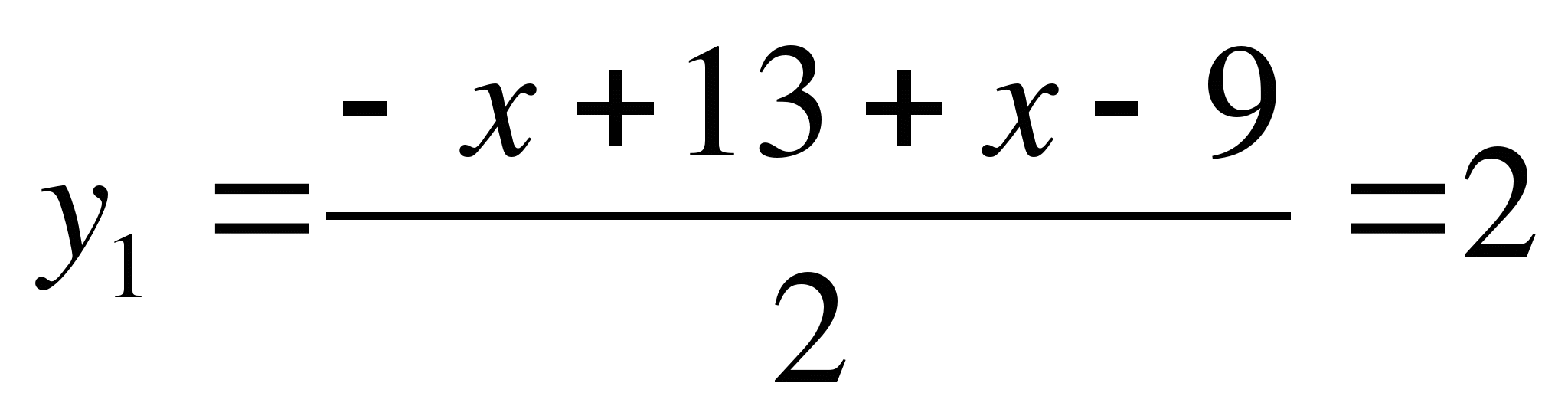
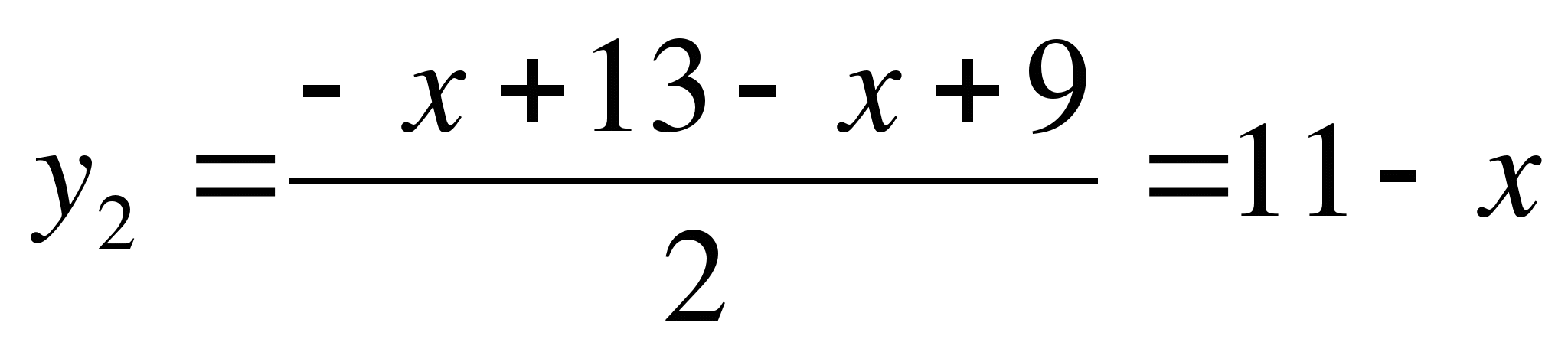
Итак, имеем:
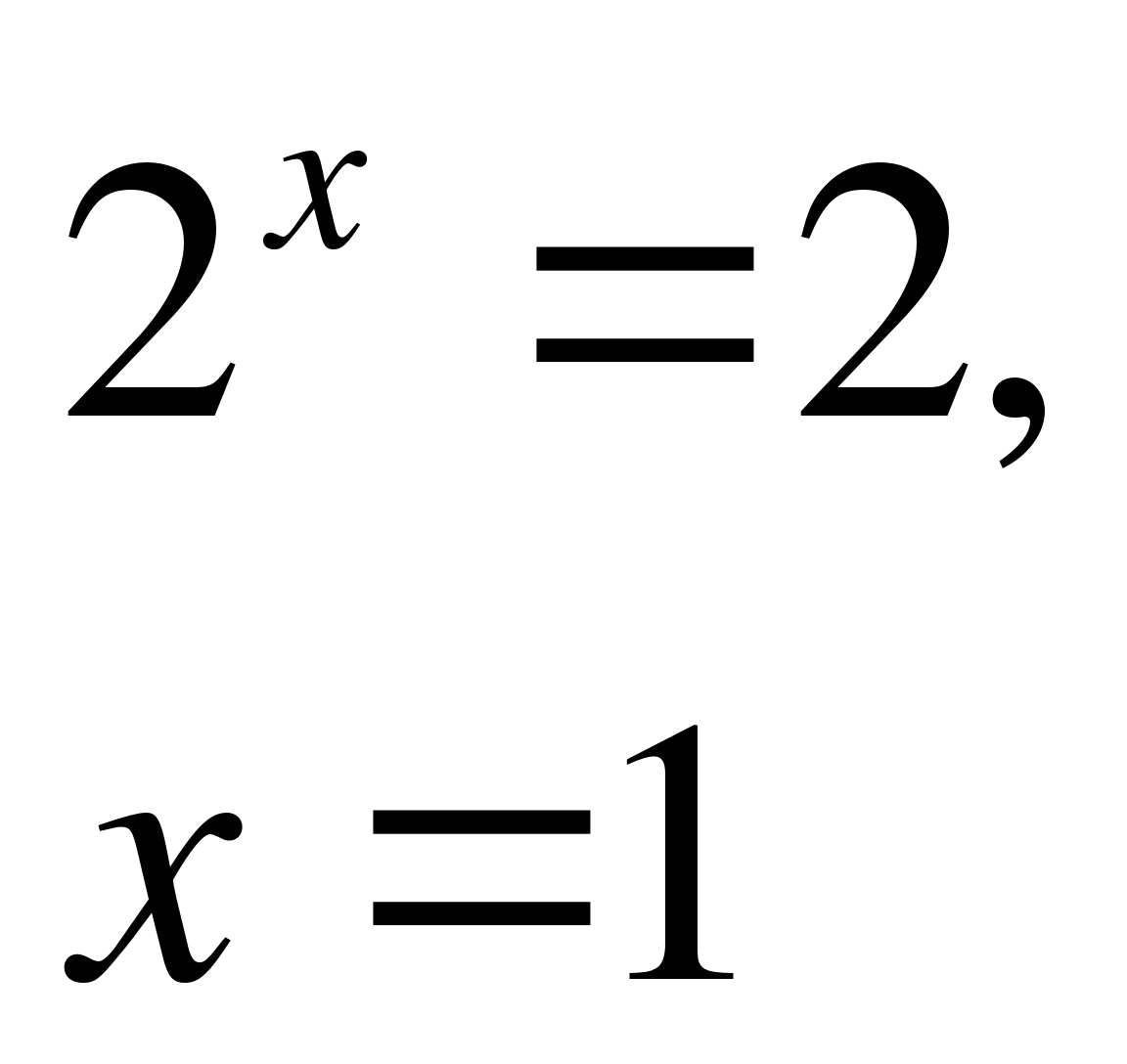 или
или
![]()
В левой части уравнения возрастающая функция,
а в правой - убывающая. Уравнение не может иметь
более одного корня.
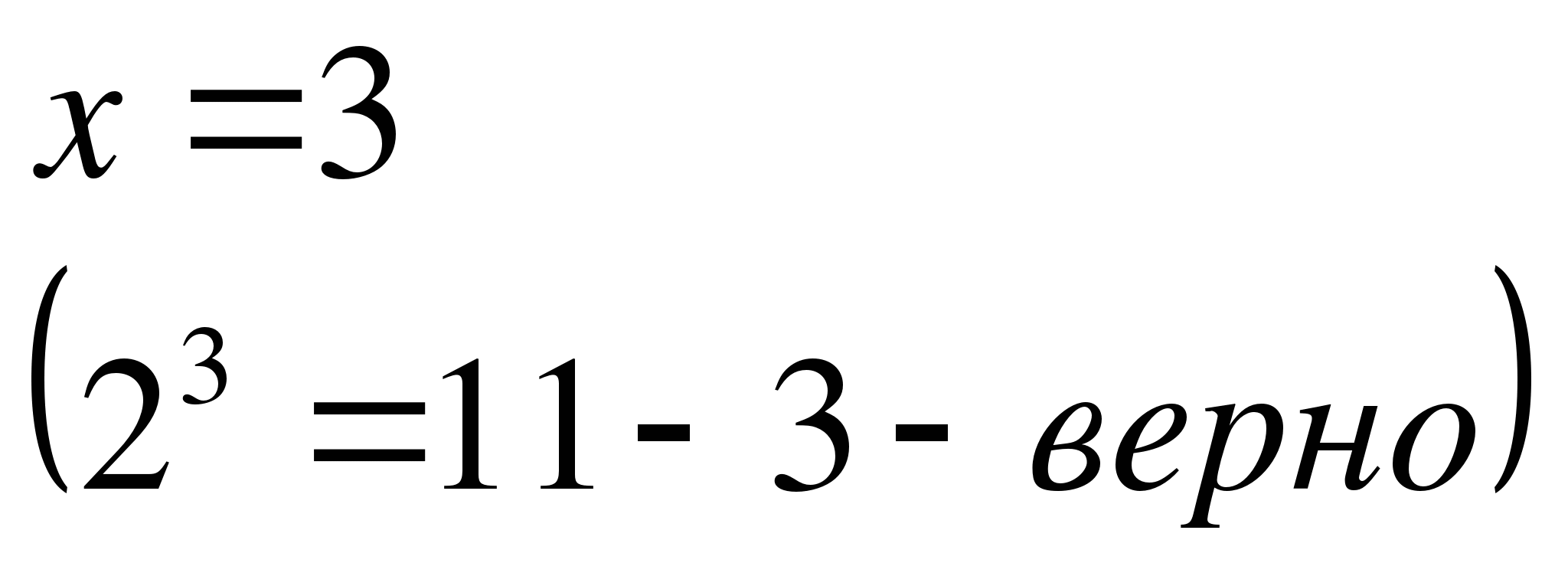
Ответ: 1; 3.
6) ![]()
Решение:
![]() ,
следовательно,
,
следовательно, ![]()
Пусть ![]() и
и ![]() .
.
Тогда ![]() .
.
![]()
Рассмотрим ![]() .
.
Наибольшее значение квадратичная функция ![]() принимает при
принимает при ![]() .
.
Таким образом, ![]() ,а
,а ![]() .
.
Данное равенство справедливо при
![]() ,
что возможно при
,
что возможно при ![]() .
.
Ответ: 0.
7)При каких значениях параметра «b» уравнение
![]() имеет
два различных корня?
имеет
два различных корня?
Решение:
Обозначим![]() .
.
![]() .
.
Для того чтобы корни ![]() и
и ![]() были положительны и различны, необходимо и достаточно:
были положительны и различны, необходимо и достаточно:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
Ответ: ![]() .
.
IV. Самостоятельная работа по выбору.
За 10 минут решить любые два (из трех) уравнения (слайдовая презентация):
1) ![]() ,
,
2) 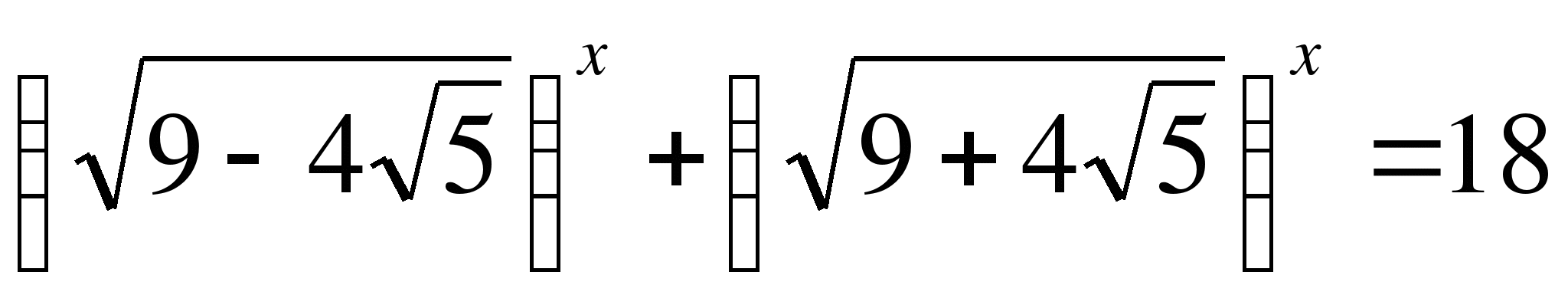 ,
,
3) ![]() .
.
На интерактивной доске приготовлены решения этих уравнений
(для сличения после 10 минут).
1) Решение:
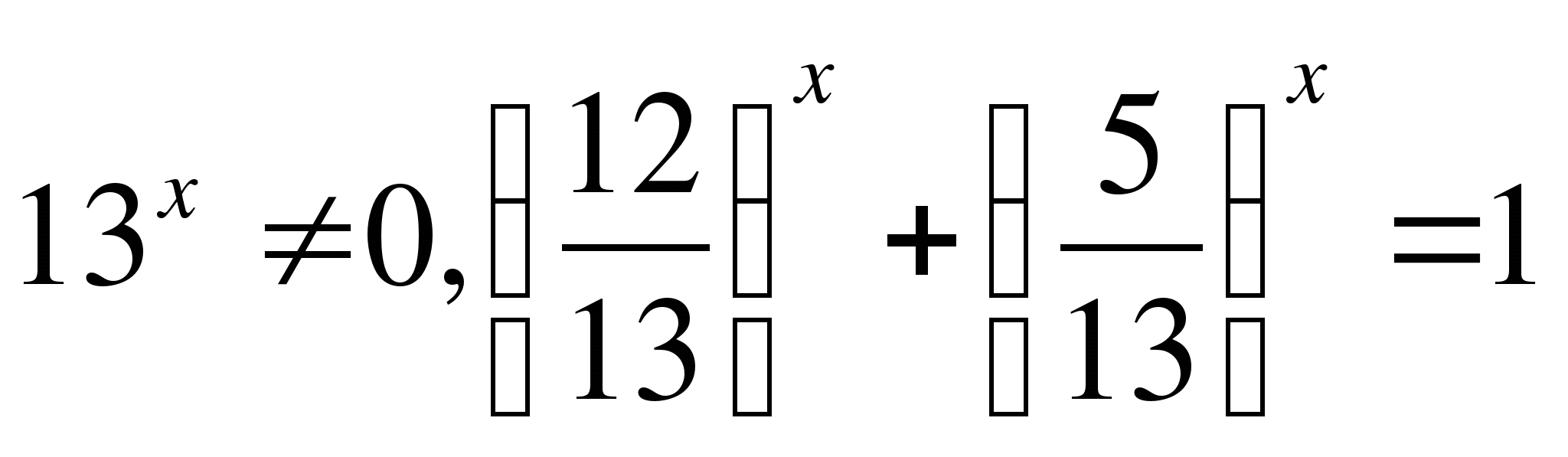 .
.
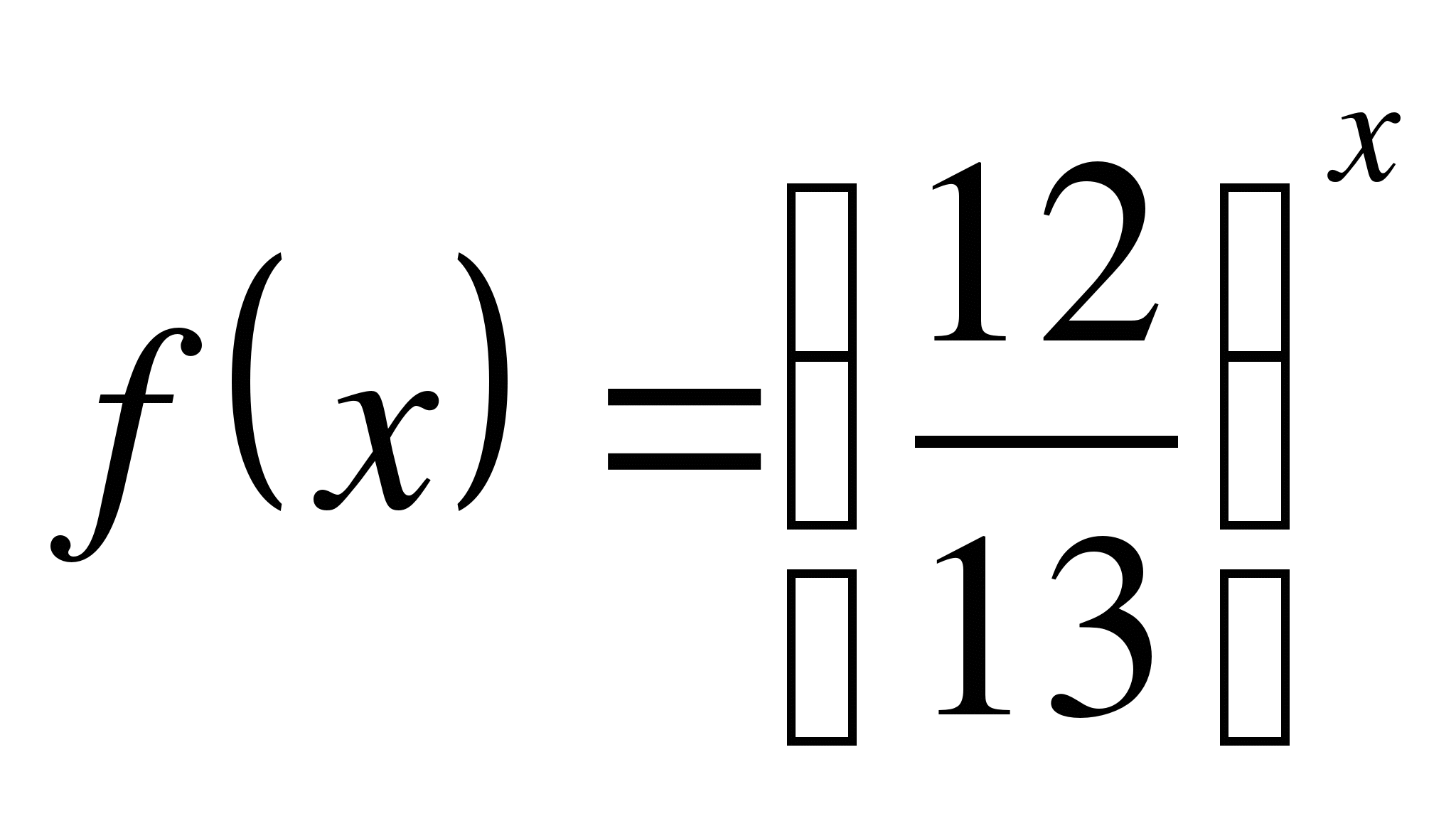 и
и
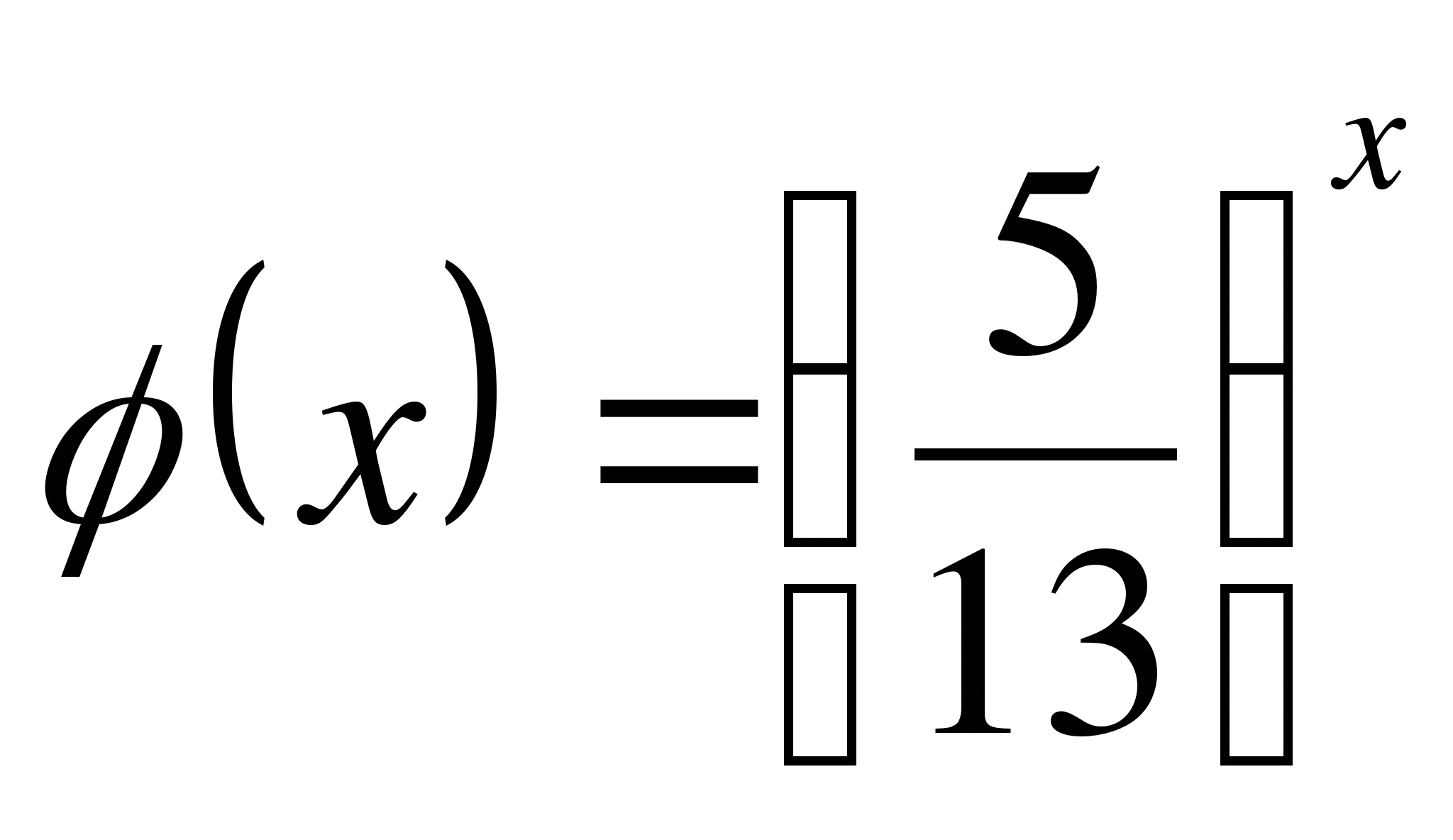 - убывающие функции на R, сумма двух убывающих функций есть функция
убывающая, поэтому уравнение
- убывающие функции на R, сумма двух убывающих функций есть функция
убывающая, поэтому уравнение 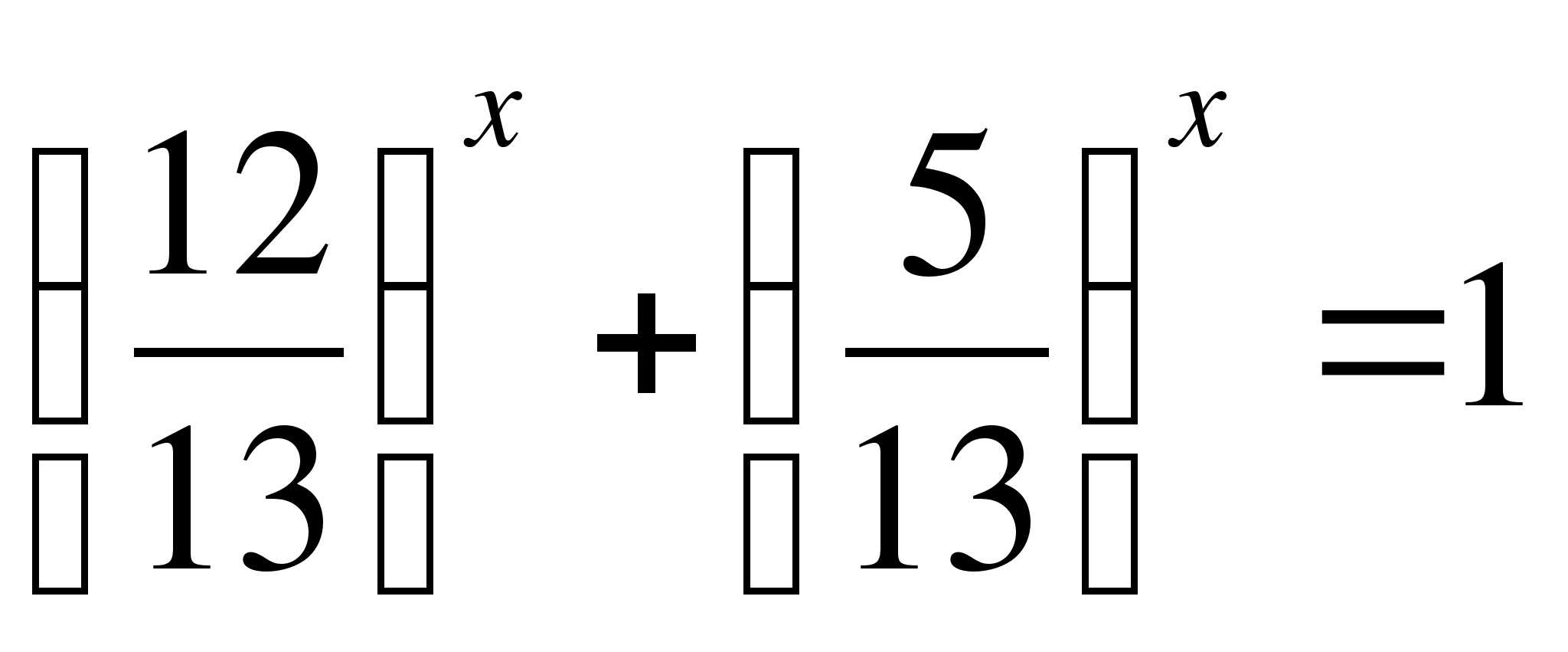 имеет единственный корень
имеет единственный корень ![]()
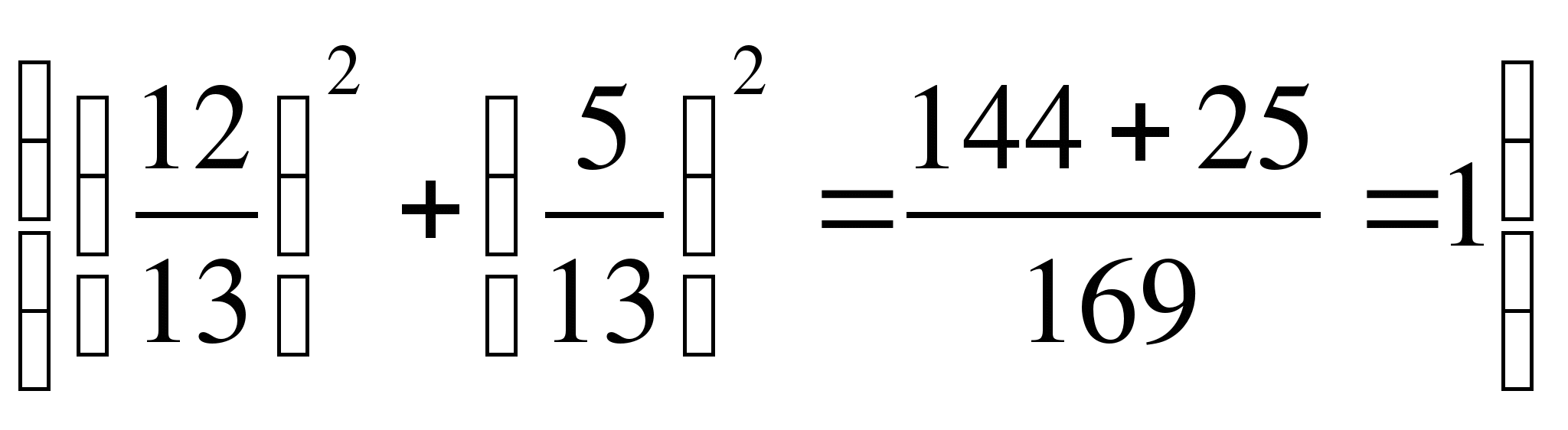 .
.
Ответ: 2.
2) Решение:
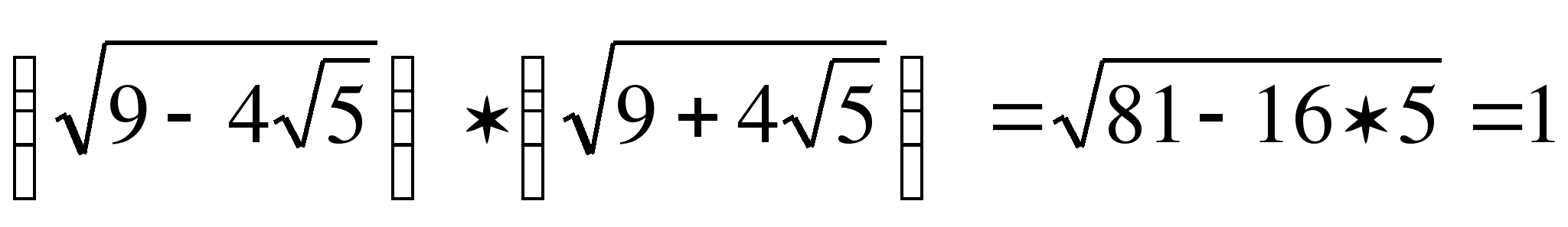 .
.
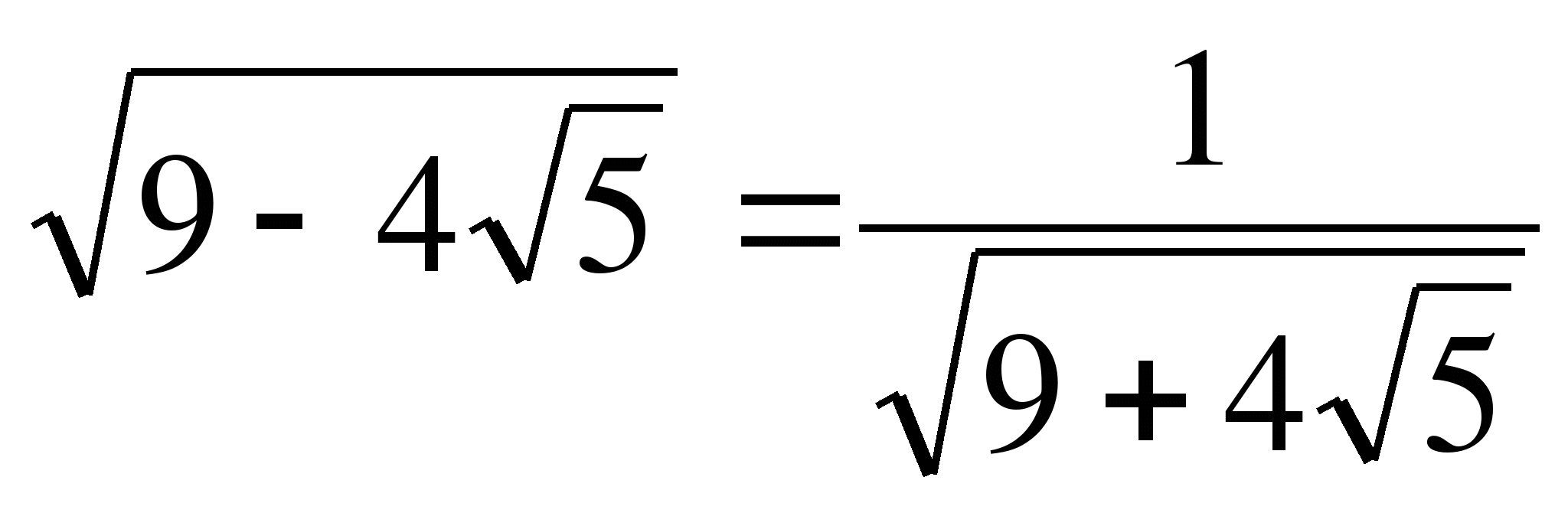 .
.
Пусть 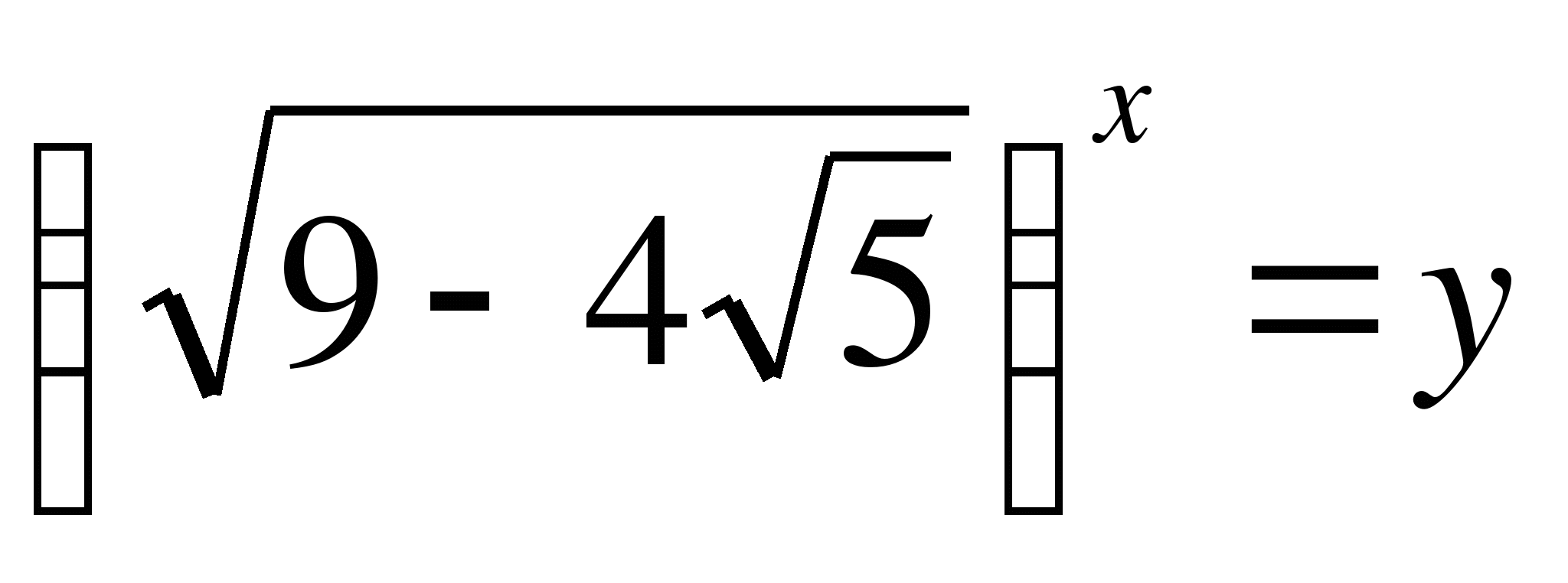 , где
, где ![]() , тогда
, тогда 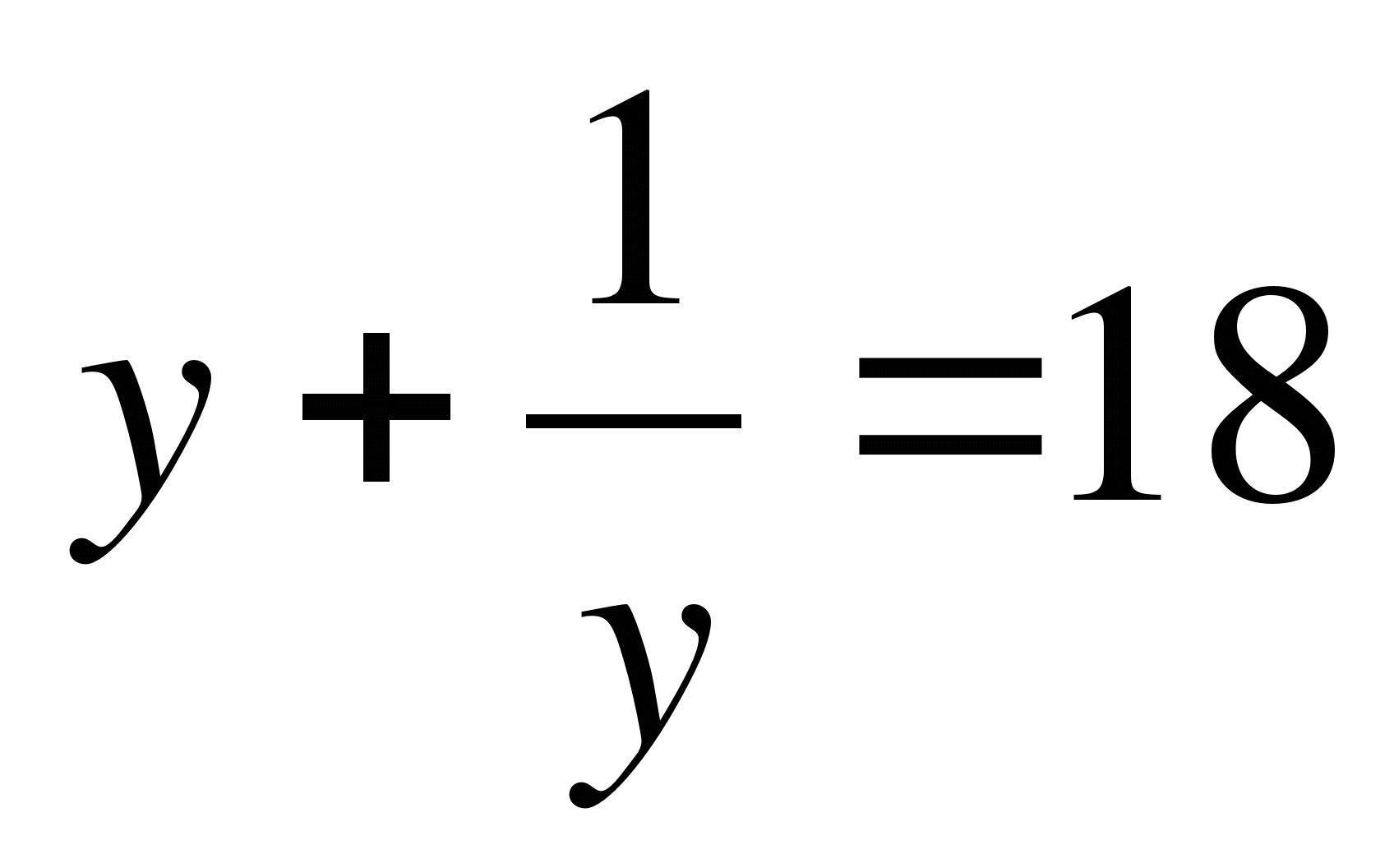 ;
;
![]() ;
;
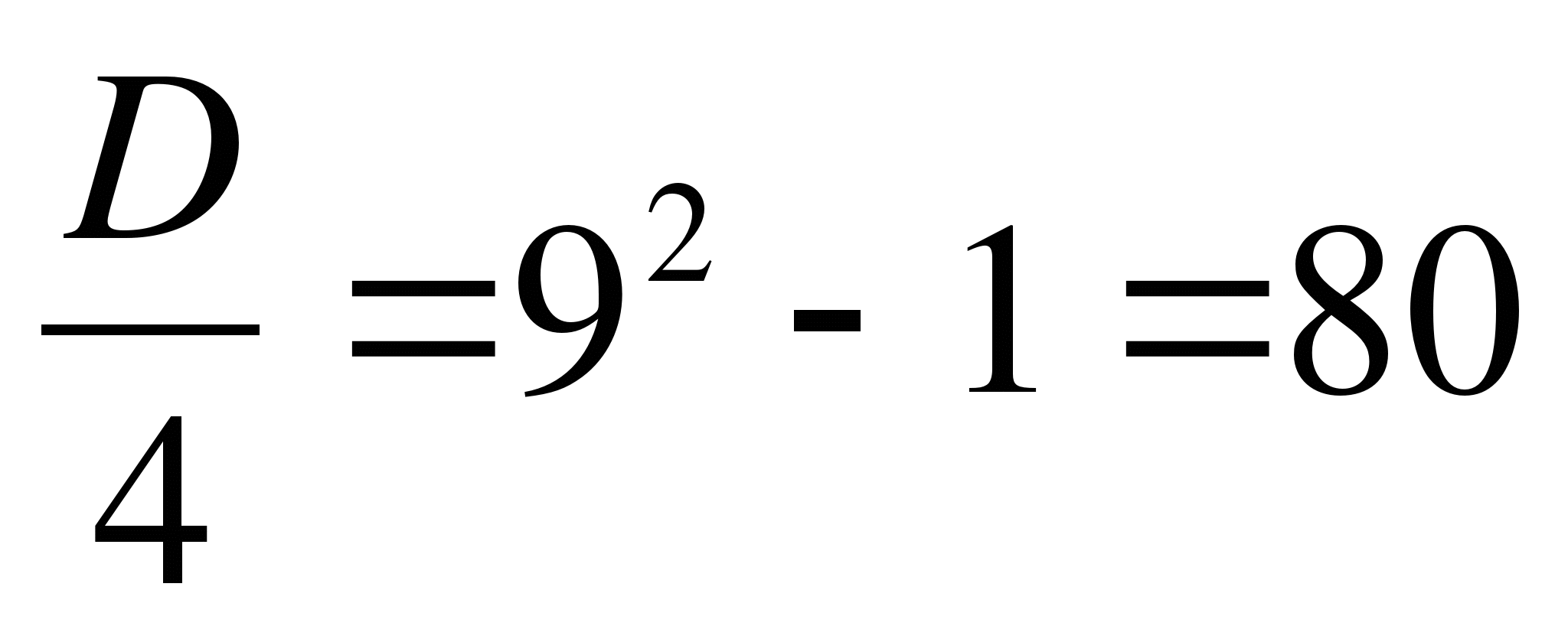 ,
,
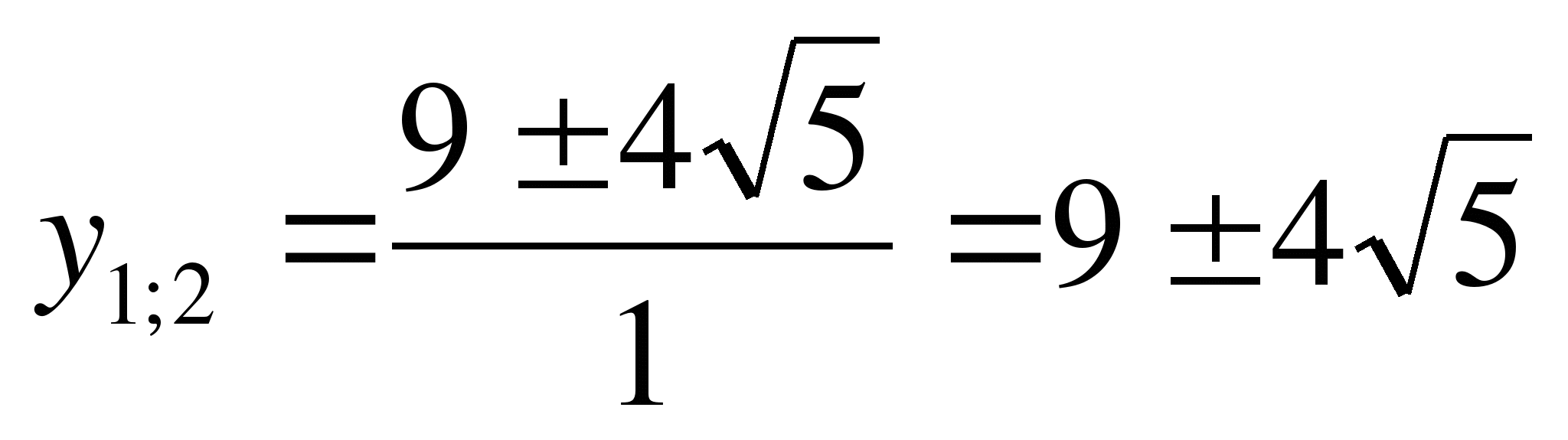 .
.
![]() ;
;
![]() ;
;
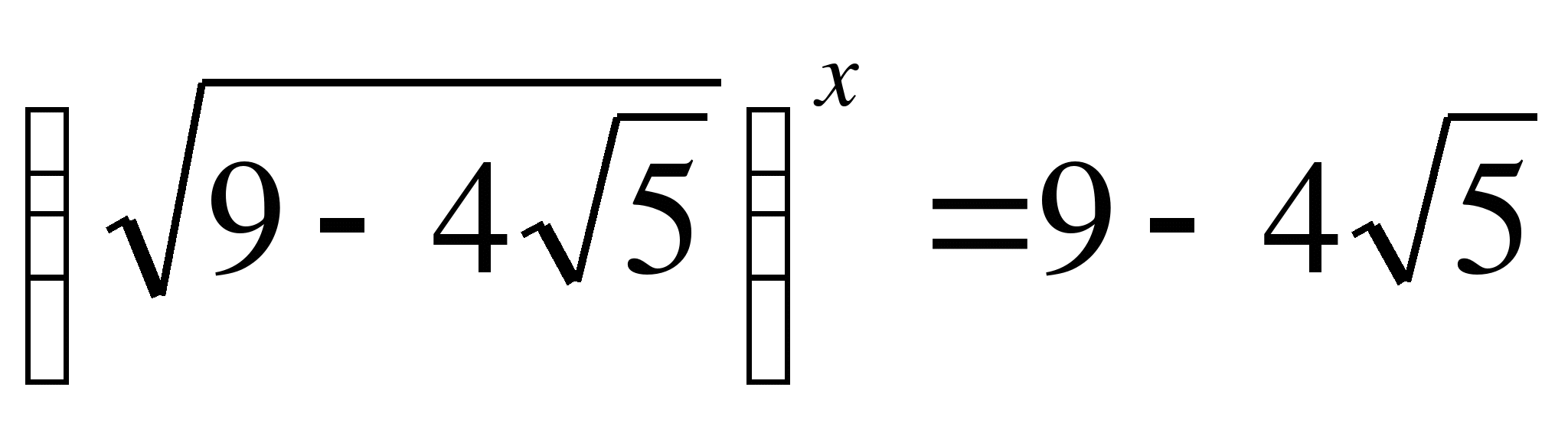 ,
или
,
или 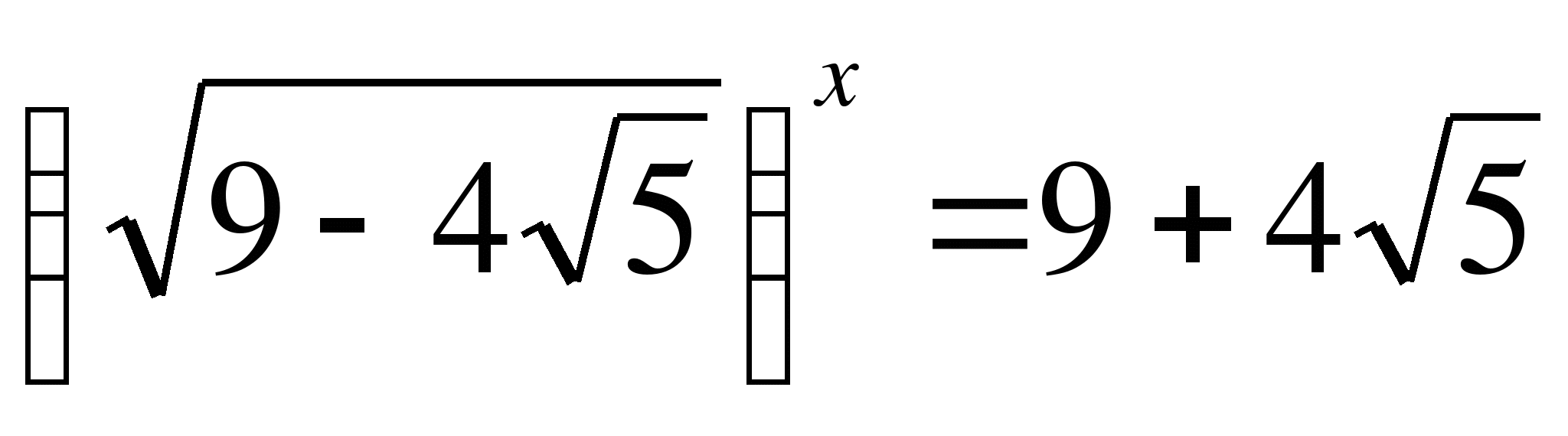 ,
,
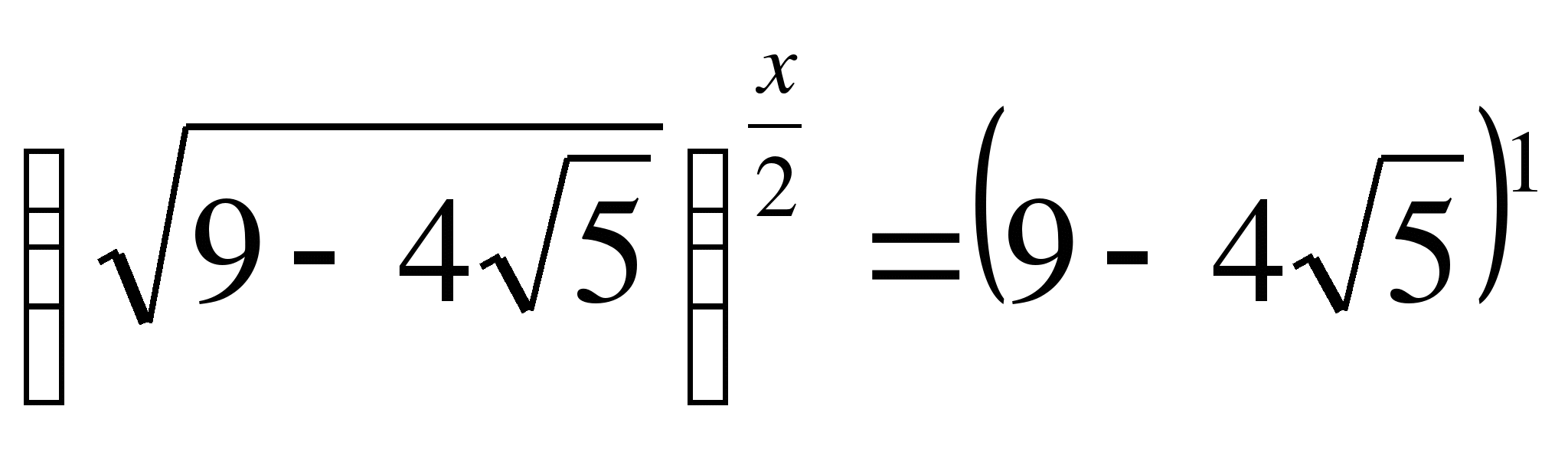 ,
,
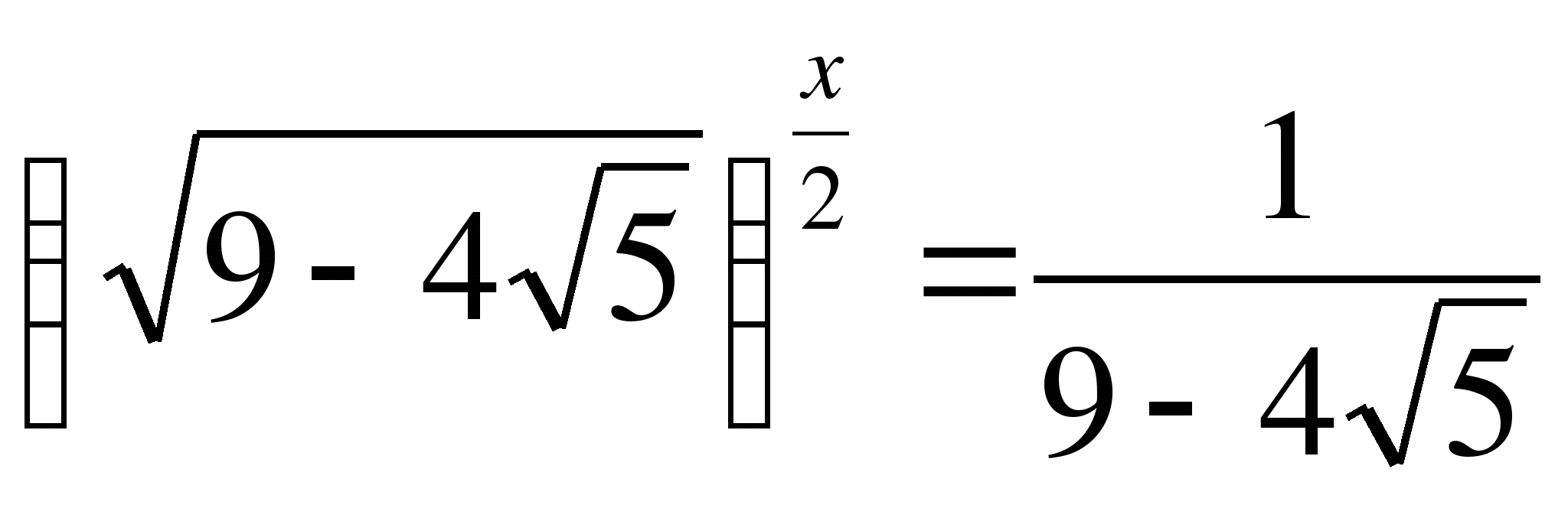 ,
,
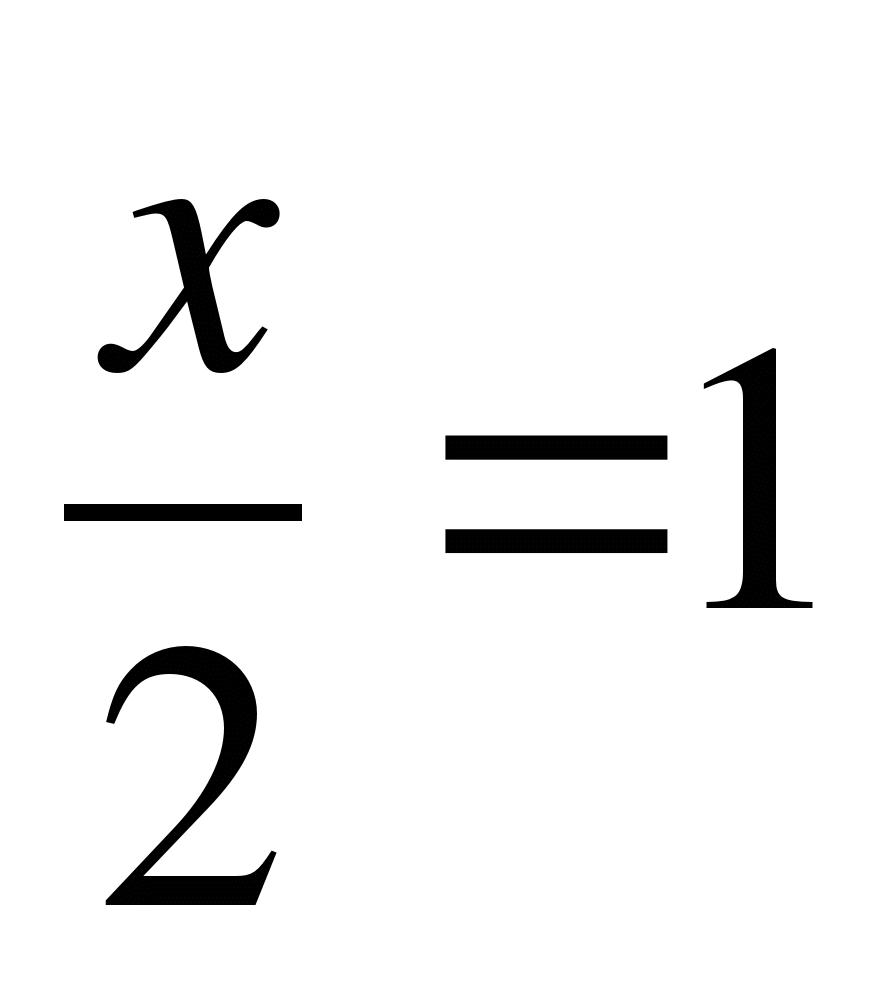 ,
,
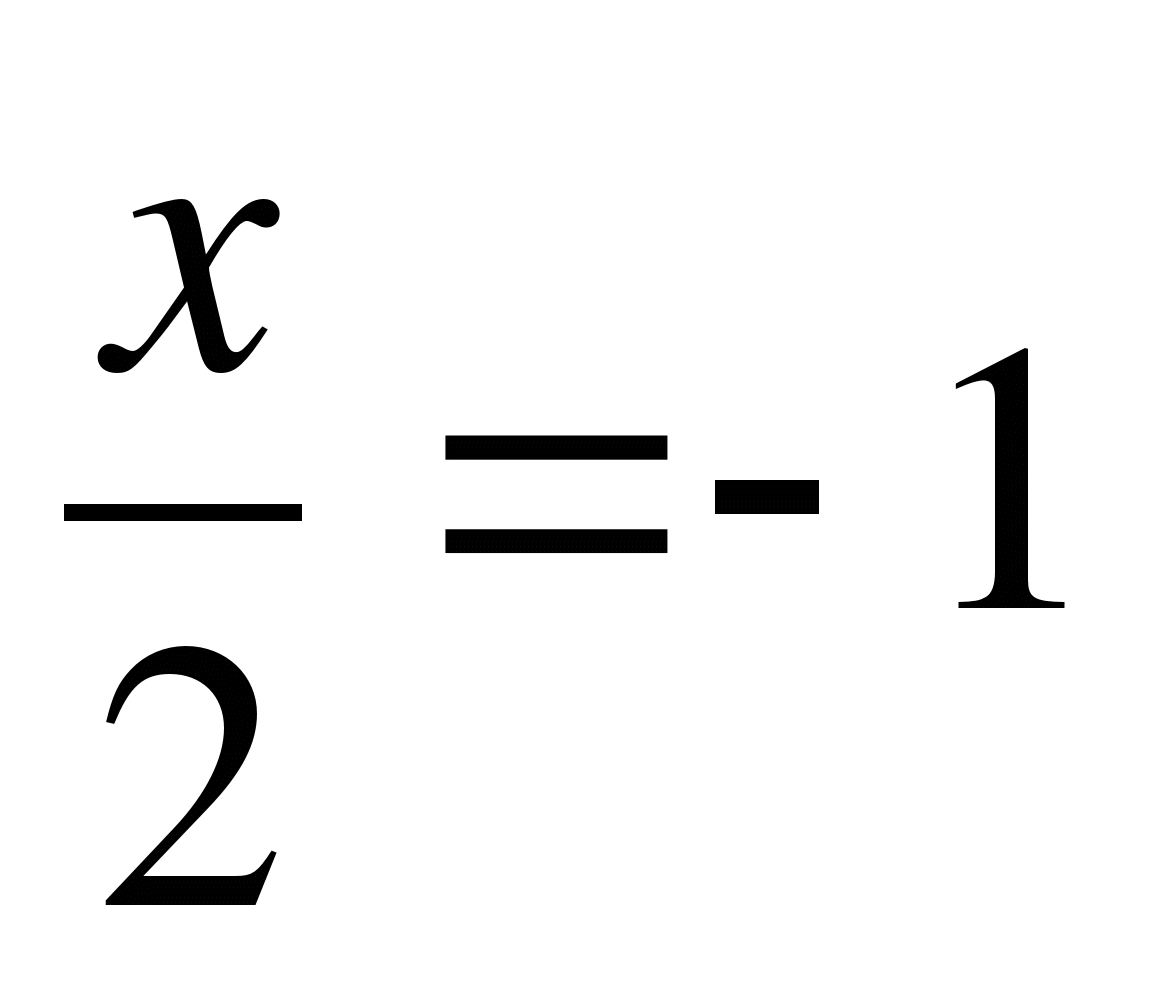 ,
,
![]()
![]() .
.
Ответ: 2; -2.
3) ![]() , разделим обе части уравнения на
, разделим обе части уравнения на ![]()
![]()
![]()
![]() .
.
Пусть ![]() , тогда уравнение примет вид:
, тогда уравнение примет вид:
![]() ,
,
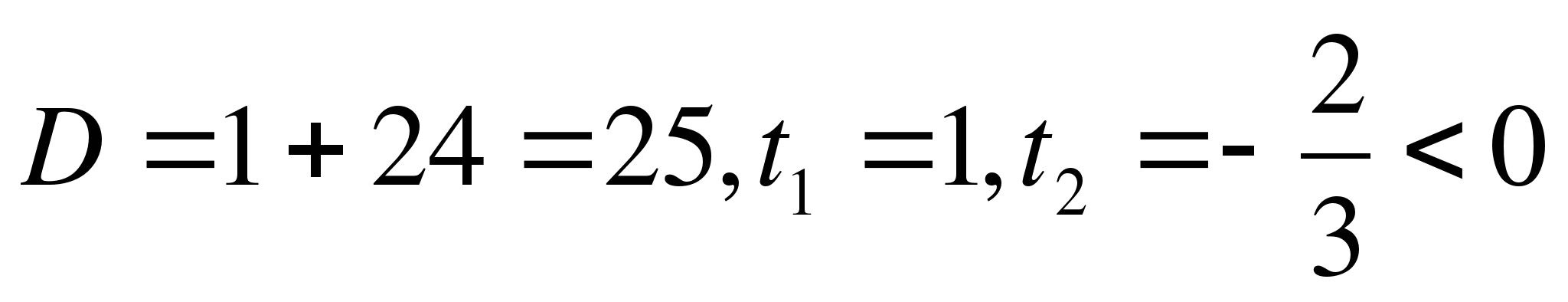 .
.
![]() ,
тогда
,
тогда ![]() .
.
Ответ: 1; 3.
V. Подведение итогов урока.
Мы рассмотрели примеры решения трансцендентных уравнений.
Огласить отметки за решение уравнений на уроке.
Задание на дом:
1) Решить уравнение:
![]() .
.
2) При каких значениях параметра «a» уравнение
![]() имеет
единственное решение?
имеет
единственное решение?
3) Решите уравнение:
![]() .
.