- Учителю
- Уравнения. Практический материал к ОГЭ по математике в 9 классе.
Уравнения. Практический материал к ОГЭ по математике в 9 классе.
МБОУ Алексеево-Лозовская СОШ
УРАВНЕНИЯ. ПРАКТИЧЕСКИЙ МАТЕРИАЛ
К ОГЭ ПО МАТЕМАТИКЕ.
-
КЛАСС
ПОДГОТОВИЛА:
учитель математики
высшей категории
МБОУ Алексеево-Лозовская СОШ
Чертковского района
Ростовской области
ШКОНДА ИРИНА АНДРЕЕВНА
Содержание.
-
Уравнения. Карточки-задания (обязательный уровень).
-
Задания для устной работы.
-
Алгоритмы решения уравнений (обязательный уровень).
-
Ответы (обязательный уровень).
-
Задания к уроку практикуму. Алгоритмы решения уравнений (повышенный уровень).
-
Задания к зачёту (повышенный уровень).
-
Ответы (повышенный уровень).
-
Приложение. Таблицы контроля.
Уравнения. Карточки-задания. Обязательный уровень.
К. № 1 ОУ Решите уравнения:
-
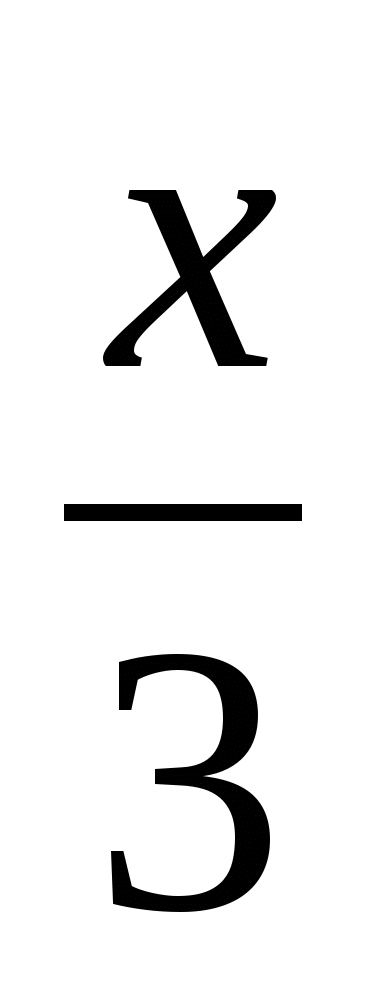 +
+  =
= 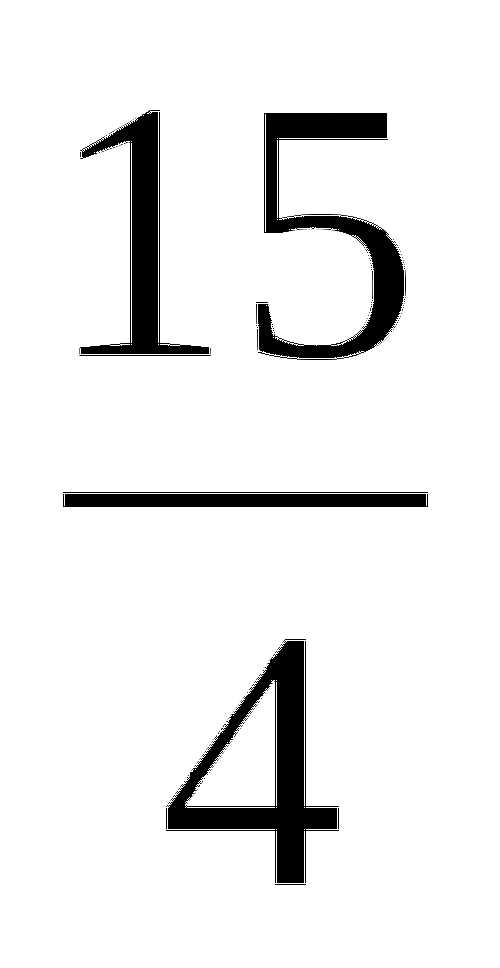
-
2 − 3(x + 2) = 5 − 2x
-
10x2 + 5x = 0
-
4 − 36x2 = 0
-
2x2 + 3x − 5 = 0
-
12 − x2 = 11
-
(10x − 4)(3x + 2) = 0
-
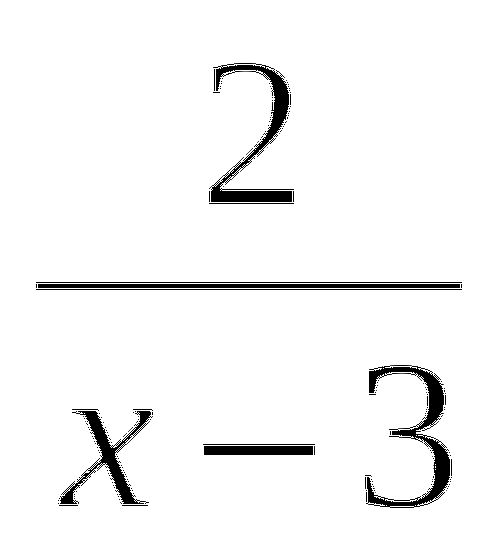 =
= 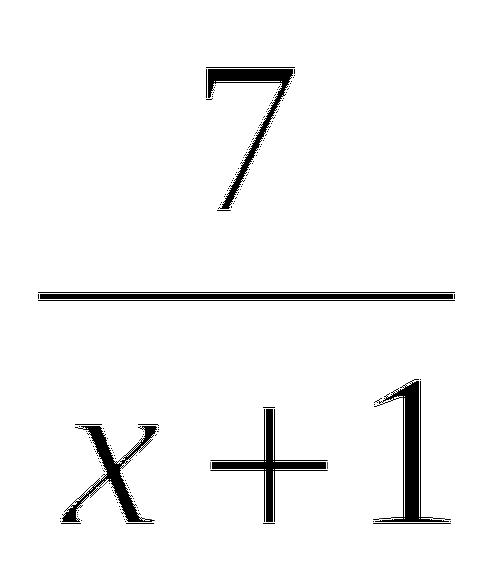
К. № 2 ОУ Решите уравнения:
-
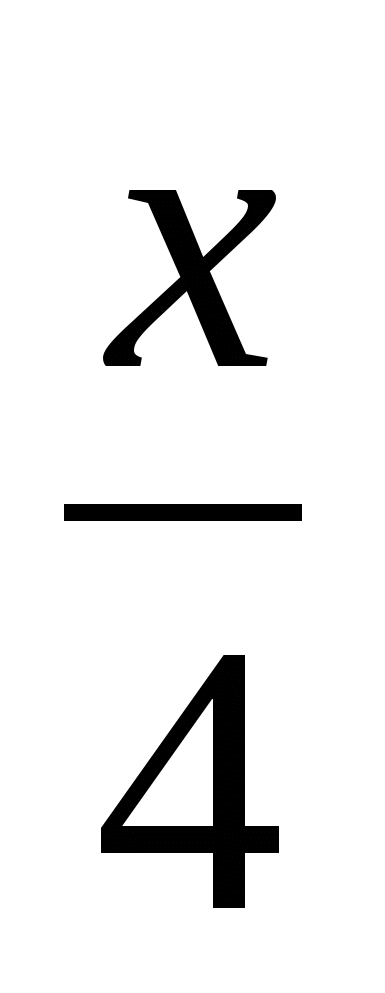 +
+ 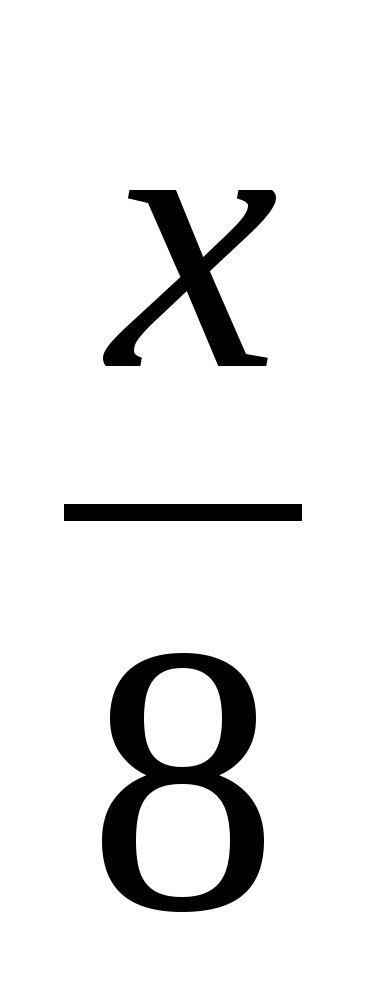 =
= 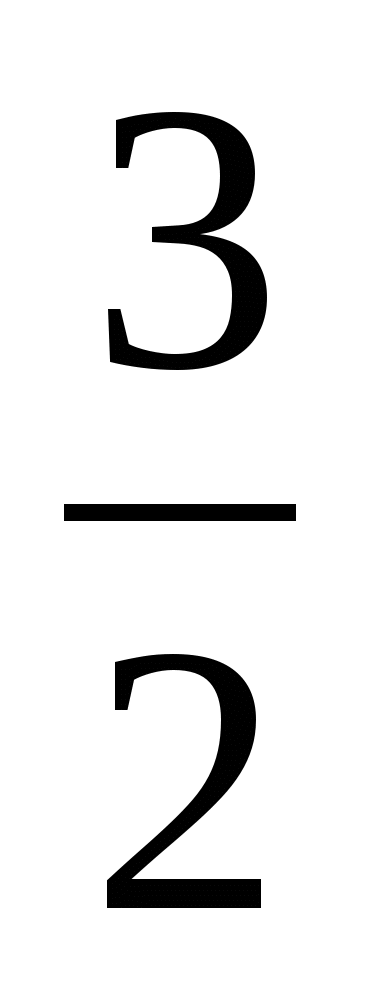
-
3 − 5(x + 1) = 6 − 4x
-
x2 − 10x = 0
-
2x2 − 10 = 0
-
2x2+ 3x − 2 = 0
-
x2 + 3 = 3 − x
-
(3x + 1)(6 − 4x) = 0
-
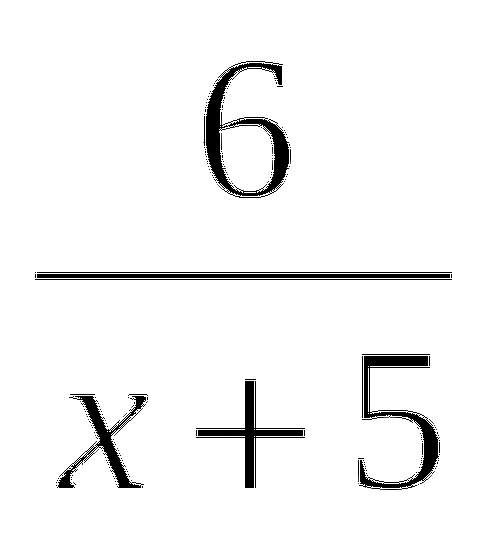 =
= 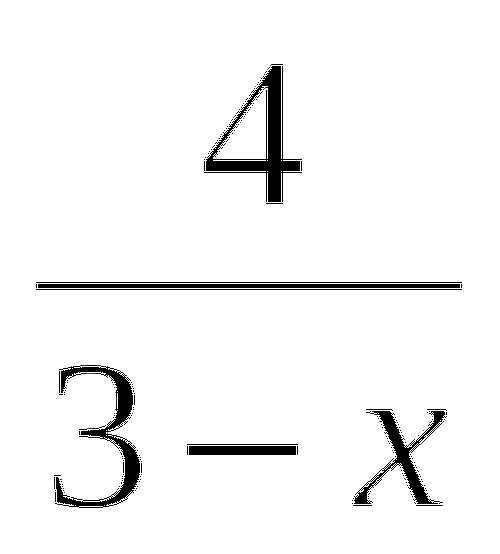
К. № 3 ОУ Решите уравнения:
-
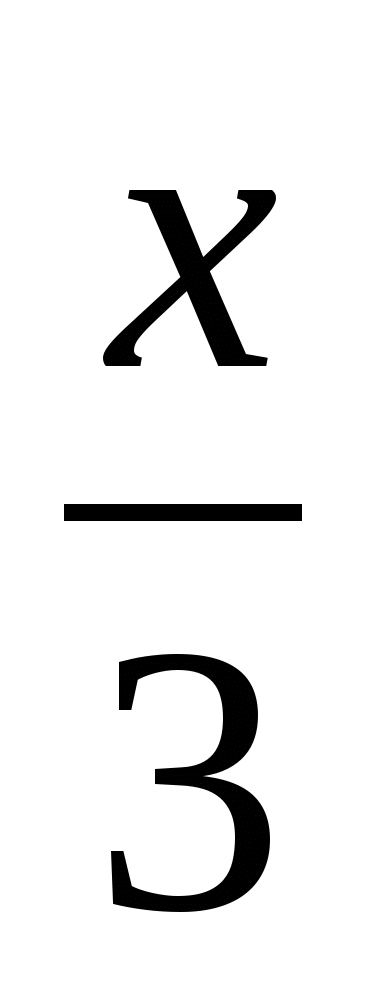 +
+ 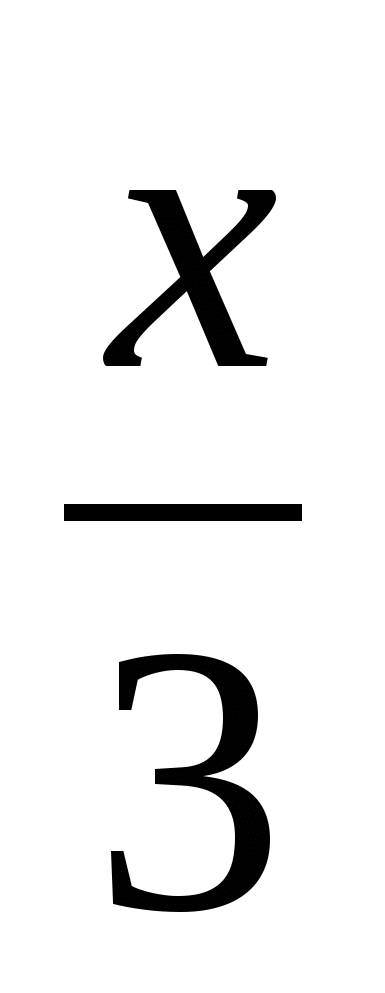 = 4
= 4 -
0,2 − 2(x + 1) = 0,4x
-
x2 + 6x = 0
-
2x2 − 8 = 0
-
3x2 + 2x − 5 = 0
-
3x2 + 9 = 12x − x2
-
(5x − 4)(x + 8) = 0
-
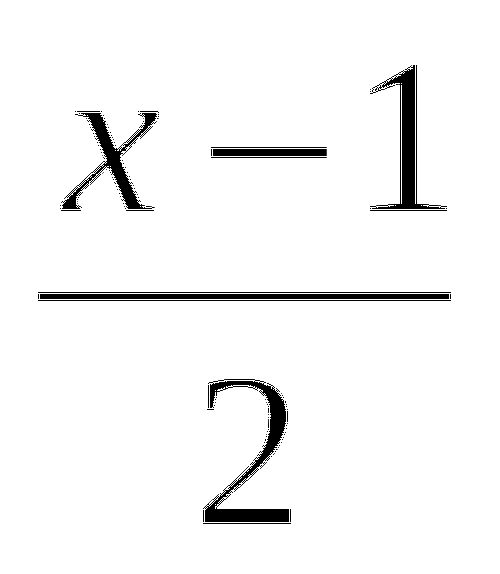 =
= 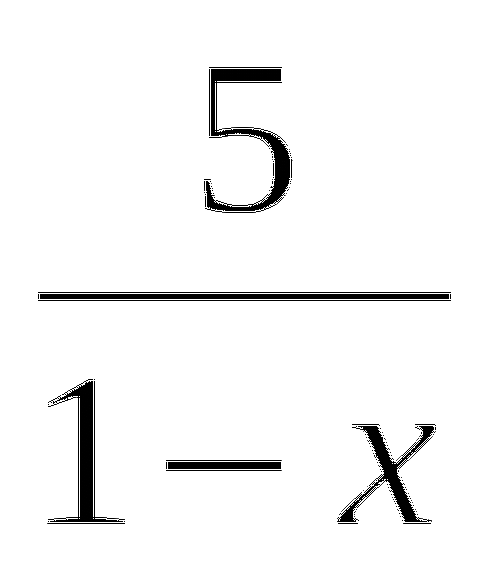
К. № 4 ОУ Решите уравнения:
-
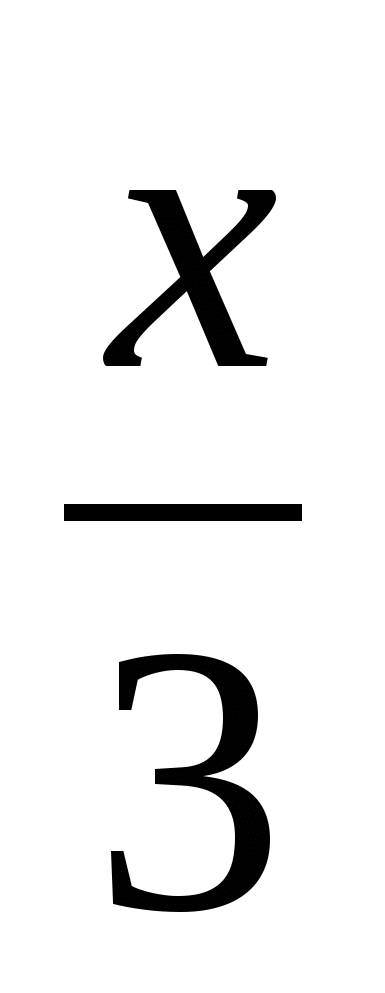 =
= 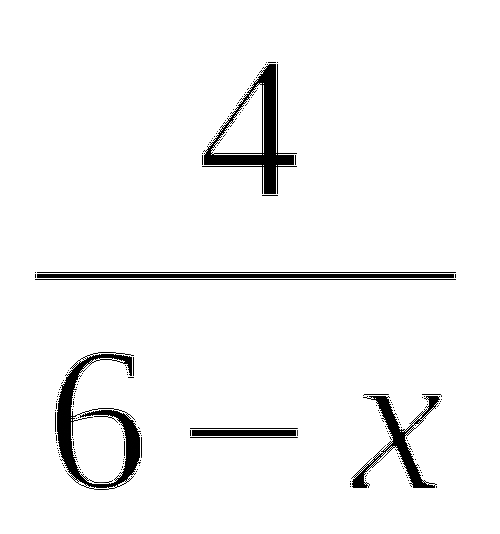
-
0,4x = 0,4 − 2(x + 2)
-
4x2 + 20x = 0
-
3x2 − 75 = 0
-
9x2 − 6x + 1 = 0
-
5x2 + 1 = 6x − 4x2
-
(6x + 3)(9 − x) = 0
-
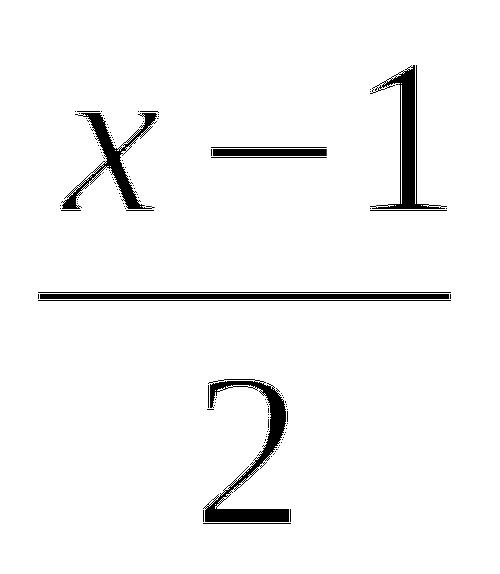 =
= 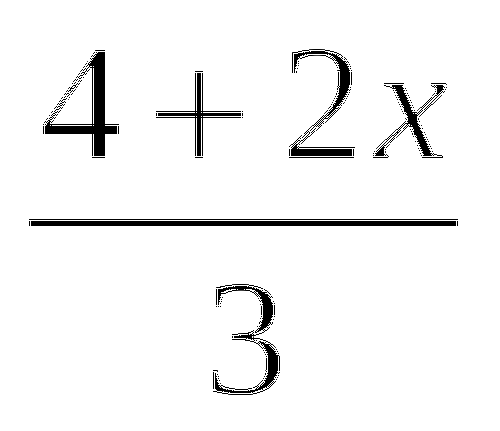
К. № 5 ОУ Решите уравнения:
-
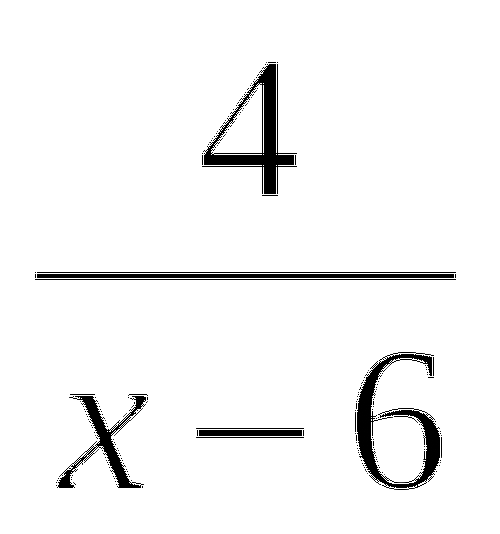 −
− 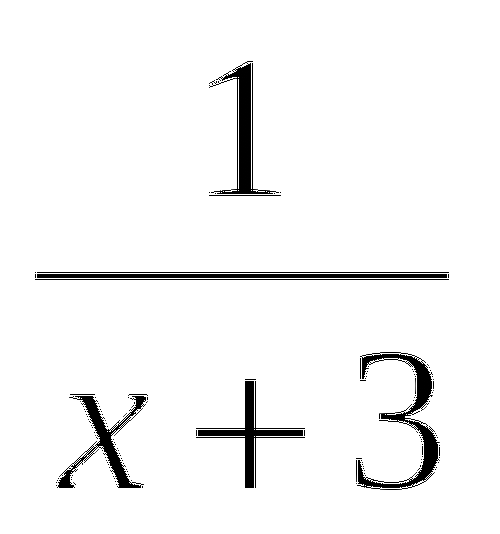 = −3
= −3 -
4x − 5,5 = 5x − 3(2x − 1,5)
-
3x2 − 12x = 0
-
3x2 − 15 = 0
-
5x2 − 3x − 2 = 0
-
x(x + 2) = 3
-
(x + 5)(2x −
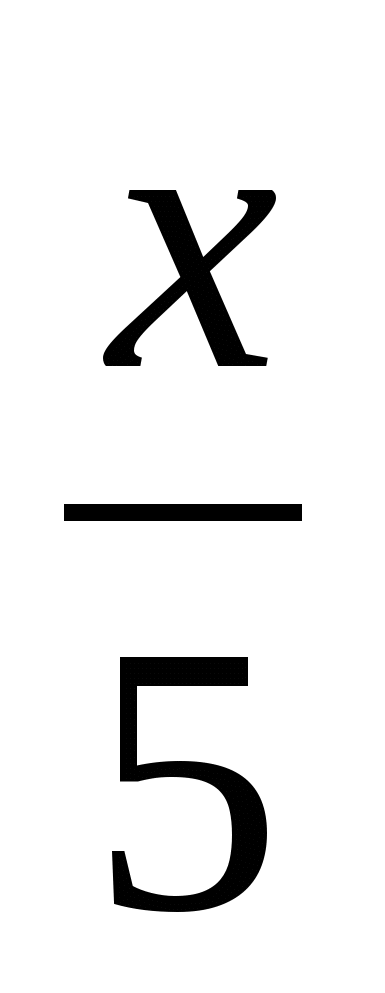 ) = 0
) = 0 -
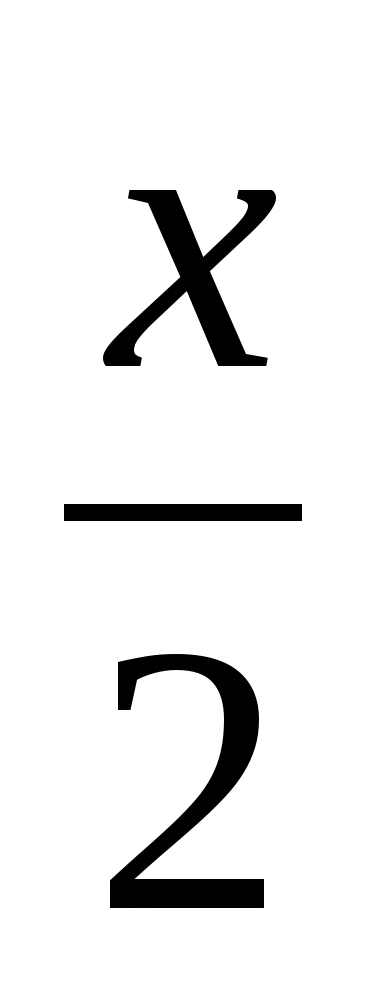 =
= 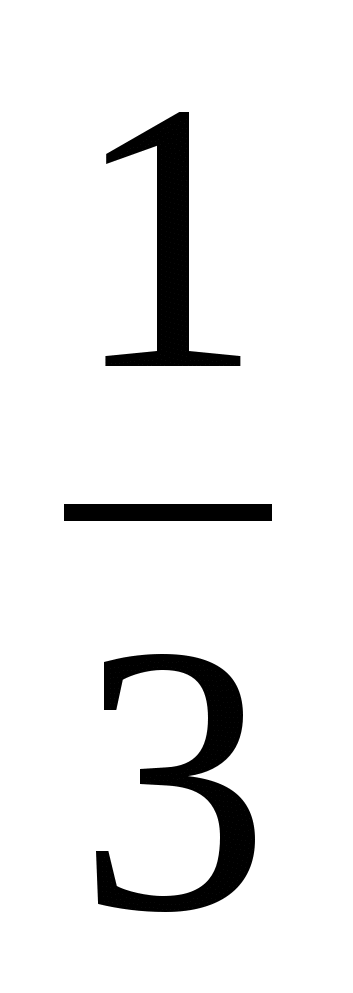
К. № ОУ Решите уравнения:
-
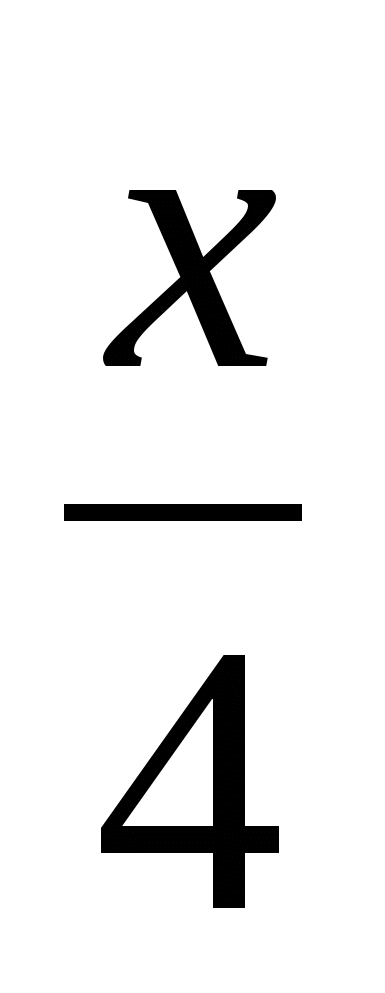 −
− 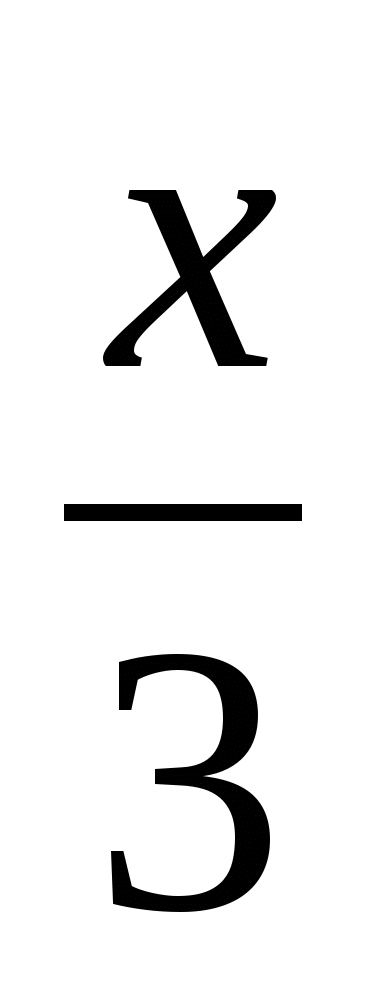 = − 1
= − 1 -
4 − 5(3x + 2,5) = 3x + 9,5
-
2x2 + x = 0
-
4x2 − 12 = 0
-
6x2 + x − 1 = 0
-
x(x + 3) = 4
-
(x − 1)(5x +
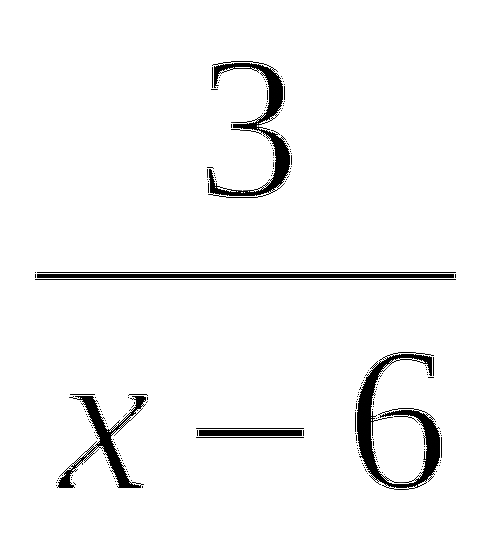 ) = 0
) = 0 -
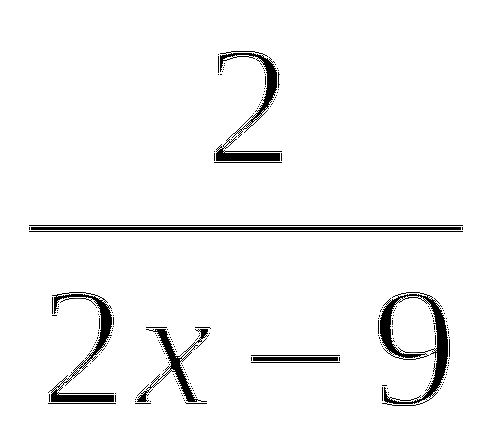 =
= 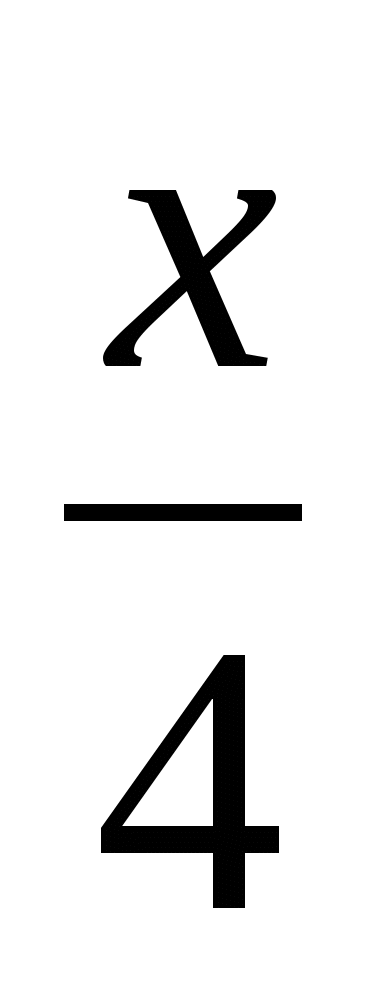
К. № 7 ОУ Решите уравнения:
-
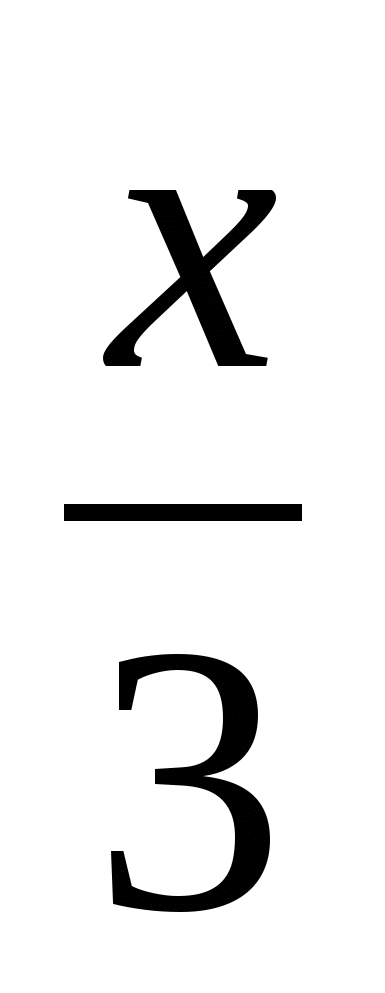 =
= 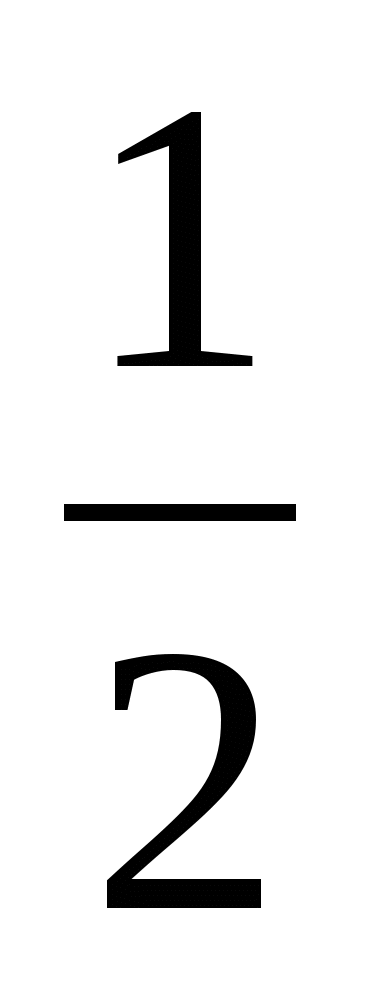
-
5(2 + 1,5x) − 0,5x = 24
-
4x2 − x = 0
-
2x2 − 32 = 0
-
5x2 − 8x + 3 = 0
-
x(2x + 1) = 3x + 4
-
6(10 − x)(3x + 4) = 0
-
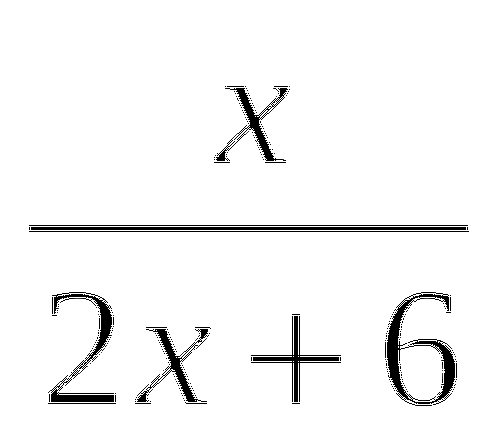 = 3
= 3
К. № 8 ОУ Решите уравнения:
-
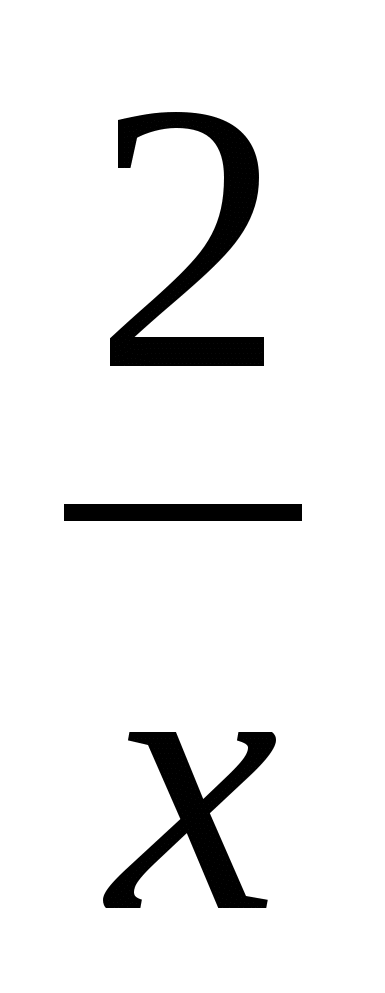 −
− 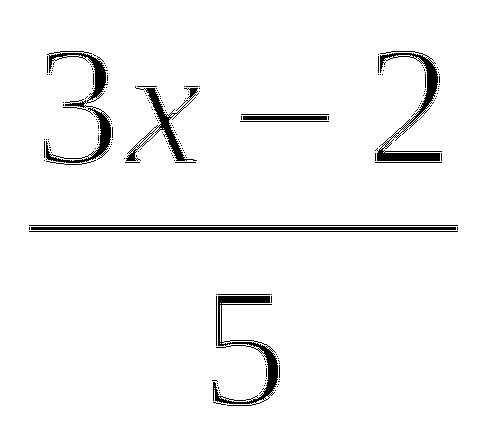 = 3
= 3 -
3(0,5x − 4) + 8,5x = 18
-
25 − 100x2 = 0
-
3x2 − 27 = 0
-
7x2+ 9x + 2 = 0
-
x2 + 2x = 16x − 49
-
2(5x − 7)(1 + x) = 0
-
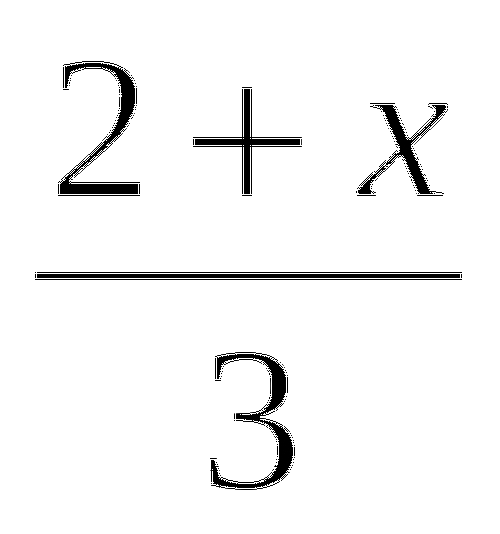 =
= 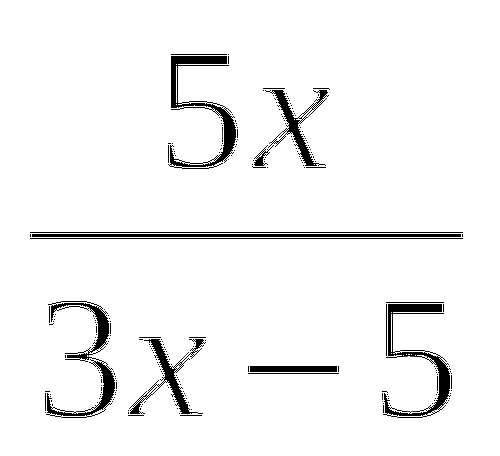
Задания для устной работы.
1. Решите неполное квадратное уравнение:
1) ![]()
6) ![]()
11) ![]()
16) ![]()
2) ![]()
7) ![]()
12) ![]()
17) ![]()
3) ![]()
8) ![]()
13) ![]()
18) ![]()
4) ![]()
9) ![]()
14) ![]()
19) ![]()
5) ![]()
10) ![]()
15) ![]()
20) ![]()
2. Решите квадратное уравнение, используя теорему Виета:![]()
![]()
1) ![]()
6) ![]()
11) ![]()
16) ![]()
2) ![]()
7) ![]()
12) ![]()
17) ![]()
3) ![]()
8) ![]()
13) ![]()
18) ![]()
4) ![]()
9) ![]()
14) ![]()
19) ![]()
5) ![]()
10) ![]()
15) ![]()
20) ![]()
3. Решите квадратное уравнение, используя формулу ![]() :
:
1) ![]()
6) ![]()
11) ![]()
16) ![]()
2) ![]()
7) ![]()
12) ![]()
17) ![]()
3) ![]()
8) ![]()
13) ![]()
18) ![]()
4) ![]()
9) ![]()
14) ![]()
19) ![]()
5) ![]()
10) ![]()
15) ![]()
20) ![]()
4. Найдите дискриминант квадратного уравнения по формуле ![]() :
:
1) ![]()
6) ![]()
11) ![]()
16) ![]()
2) ![]()
7) ![]()
12) ![]()
17) ![]()
3) ![]()
8) ![]()
13) ![]()
18) ![]()
4) ![]()
9) ![]()
14) ![]()
19) ![]()
5) ![]()
10) ![]()
15) ![]()
20) ![]()
![]() 5. Сколько корней имеет квадратное уравнение, если
5. Сколько корней имеет квадратное уравнение, если ![]() равно:
равно:
1) ![]()
6) ![]()
11) ![]()
16) ![]()
2) ![]()
7) ![]()
12) ![]()
17) ![]()
3) ![]()
8) ![]()
13) ![]()
18) ![]()
4) ![]()
9) ![]()
14) ![]()
19) ![]()
5) ![]()
10) ![]()
15) ![]()
20) ![]()
6. Решите квадратное уравнение:
1) ![]()
6) ![]()
11) ![]()
16) ![]()
2) ![]()
7) ![]()
12) ![]()
17) ![]()
3) ![]()
8) ![]()
13) ![]()
18) ![]()
4) ![]()
9) ![]()
14) ![]()
19) ![]()
5) ![]()
10) ![]()
15) ![]()
20) ![]()
1) ![]()
Решение
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
Ответ: ![]() .
.
8) ![]()
Решение
![]() ,
, ![]() ;
; ![]() .
.
![]() ;
; ![]() ;
; ![]() .
.
Ответ: ![]() .
.
2) ![]()
Решение
![]() .
. ![]() .
.
![]() ;
; ![]() .
.
![]() ;
; ![]() .
.
Ответ: ![]() .
.
9) ![]()
Решение.
О.Д.З. уравнения: ![]() .
.
Умножим обе части уравнения на ![]() , получим:
, получим: ![]() ;
;
![]() ;
; ![]() . Ответ:
. Ответ: ![]() .
.
3) ![]()
Решение
![]() .
.
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Ответ: ![]() .
.
10) ![]()
Решение
Умножим обе части уравнения на число ![]() .
.
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Ответ: ![]() .
.
4) ![]()
Решение
![]() ;
; ![]() ;
; ![]() .
.
Ответ: ![]() .
.
11) ![]()
Решение
а) ![]() ;
; ![]() ;
; ![]() ;
;
б) ![]() ;
; ![]() .
.
Ответ: ![]() .
.
5) ![]()
Решение
![]() ;
; ![]() .
.
Ответ: ![]() .
.
12) ![]() .
.
Решение
О.Д.З. уравнения ![]() ,
, ![]() .
.
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
Ответ: ![]() .
.
6) ![]()
Решение
![]() .
.
Ответ: ![]()
![]() .
.
13*) ![]() .
.
Решение
![]() ;
; ![]() ;
; ![]() .
.
а)![]() ;
; ![]() .
.
7) ![]()
Решение
а) ![]() ;
;
б) ![]() . Ответ:
. Ответ: ![]() .
.
14*) ![]() ;
;![]() ;
;
О.Д.З.: ![]()
![]() ;
;![]() ;
;![]() ;
;![]() .
.
Ответ: ![]() .
.![]() Уравнения ОУ. Алгоритмы решения уравнений.
Уравнения ОУ. Алгоритмы решения уравнений.
Ответы. Уравнения. Обязательный уровень.
К.№ 1
К.№ 2
К.№ 3
К.№ 4
К.№ 5
К.№ 6
К.№ 7
К.№ 8
1
9
4
5,4
-11
10
12
4
16
2
-9
-8
-0,75
-1,5
2
-1
2
3
3
-0,5; 0
0; 10
-6; 0
-5; 0
0; 4
-0,5; 0
0; 025
![]()
4
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5
-2,5; 1
-2; 0,5
![]() ; 1
; 1
![]()
-0,4; 1
![]()
![]()
![]()
6
![]()
-1; 0
1,5
![]()
-3; 1
-4; 1
-1; 2
-1; 1,4
7
![]()
![]()
-8; 0,8
-0,5; 9
-5;![]()
-0.1; 1
10; ![]()
-1; 1,4
8
4,6
-0,2
26
-6
3,75
-2,6
3,75
2,6
Уравнения. Практикум. Задания повышенного уровня.
Метод разложения на множители
Учеб.(№272е) 1.Решить уравнение:![]() .
.
Решение. ![]() ;
; ![]() ;
; ![]() ;
;
![]()
![]()
![]() ;
; ![]() .
.
Ответ: -4; 0; 1; 4.
ГИА 9 (Лысенко Ф.Ф.) (111) 2. Решить уравнение: ![]() .
.
Решение. ![]() ;
; ![]()
![]() ;
; ![]() ;
;
![]() .
.
Реши сам. Уч. Алгебра 9 (Ю.Ш. Макарычев ) №272д,з; ГИА 9 математика (Ф.Ф. Лысенко) №109-110.
№109: ![]() ; №110:
; №110: ![]() ;№272д:
;№272д: ![]() ;
;
№272з: ![]() . Ответы: №109: 0;2,5 №110: 0;-2;2;-1,5. №272д:
. Ответы: №109: 0;2,5 №110: 0;-2;2;-1,5. №272д:![]() ; №272з: 0;
; №272з: 0;![]() .
.
Метод замены переменной
Учеб.(№277в) 1.Решить уравнение: ![]() ;
;
Решение. ![]() ;
; ![]()
![]()
![]() По т. Обр. т.Виета
По т. Обр. т.Виета
![]() (
(![]() . Вернёмся к замене,
. Вернёмся к замене,
а) ![]()
![]() корней нет.
корней нет.
б) ![]()
![]() два корня.
два корня. ![]() . Ответ: -4; 3.
. Ответ: -4; 3.
Реши сам. Уч. Алгебра 9 (Ю.Ш. Макарычев ) №277б; ГИА 9 математика (Ф.Ф. Лысенко) №128№130.
№277б: ![]() ; №128:
; №128:![]() ; №130:
; №130:![]() . Ответы: №277б: 2; №128: 2; 4. №130:
. Ответы: №277б: 2; №128: 2; 4. №130: ![]() .
.
Дробные рациональные уравнения
ГИА 9 м. (Ф.Ф. Лысенко) №105: 1.Решить уравнение: ![]() .
.
Решение. ![]() .
.
1) Разложим кв. трёхчлены![]()
![]() на множители по формуле
на множители по формуле
![]() .
. ![]()
![]() .
.
-
ОДЗ уравнения
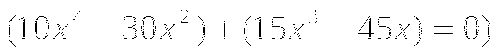
-
Умножим обе части уравнения на
 получим
получим
![]()
![]()
![]()
![]()
Оба корня удовлетворяют ОДЗ уравнения. Ответ: 2; 9.
Реши сам. Уч. Алгебра 9 (Ю.Ш. Макарычев ) №290б;№291б;
ГИА 9 математика (Ф.Ф. Лысенко) №106№120№121.
Уч. А 9 (Ю.Ш. Макарычев ) №290б: 1.Решить уравнение ![]()
ГИА 9 м. №106: ![]() №120:
№120: ![]() №121
№121
![]() Ответы: №290б: 0; №106: -3; 4. №120: 4; №121: 1.
Ответы: №290б: 0; №106: -3; 4. №120: 4; №121: 1.
Уравнения. Повышенный уровень. Задания к зачёту.
Задания.
Решите уравнения:
1.Биквадратные уравненния
1)![]() ; 2)
; 2)![]() ;
;
3)![]() : 4)
: 4)![]() .
.
2.Метод разложения на множители
1) ![]() ; 2)
; 2) ![]() ;
;
3) ![]() ; 4)
; 4) ![]()
3.Метод замены переменной
1)![]() ; 2)
; 2) ![]() .
.
3) ![]() ; 4)
; 4) ![]()
4. Дробные рациональные уравнения
1) ![]() ; 2)
; 2) ![]() ;
;
3) ![]() ; 4)
; 4) ![]() .
.
*5. Дробные рациональные уравнения
1) ![]() ; 2)
; 2) ![]() ;
;
3) ![]() ; 4)
; 4) ![]() .
.
* 6.Метод замены переменной
1) ![]() ; 2)
; 2) ![]() ;
;
3)![]() ; 4)
; 4) ![]() .
.
**7 Уравнения с параметром
1) При каких значениях а корни уравнения: x2 - 2ax + (a + 1)(a - 1) = 0 принадлежат промежутку [− 5; 5]?
2) При каких значениях p корни уравнения: x2 - 2(p + 1)x + p(p + 2) = 0 принадлежат промежутку [− 1; 3]?
3) При каких значениях b уравнение x2 + 2(b + 1)x + 9 = 0 имеет два различных положительных корня?
4) При каких значениях k уравнение x2 - 4x + (2 - k)(2 + k) = 0 имеет корни разных знаков?
**Уравнения
1)Не вычисляя корней x1 и x2 уравнения x2 − 7x − 21 = 0, найдите значение выражения: x12 + x22.
2) x1 = −3 является корнем уравнения 5x2 + 12x + q = 0. Найдите x2, q.
3) Сумма квадратов корней уравнения x2 + px − 3 = 0 равна 10. Найдите значение числа p.
4)Не вычисляя корней x1, x2 уравнения x2 − 7x + 12 = 0, найдите значение выражения: x12 + x22.
Указание: ![]()
![]()
![]() прив.ур. или
прив.ур. или ![]() ).
).
Уравнения. Повышенный уровень. Ответы
Ответы
Уравнения:
1.Биквадратные уравненния
1)![]() ; 2)
; 2)![]() ; 3)
; 3)![]() : 4)
: 4)![]() .
.
2.Метод разложения на множители
1) ![]() ; 2)
; 2)![]() ; 3)
; 3)![]() ; 4)
; 4) ![]() .
.
3.Метод замены переменной
1)![]() . 2)
. 2)![]() . 3)
. 3) ![]() . 4)
. 4)![]() .
.
4.Дробные рациональные уравнения
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
*5.Дробные рациональные уравнения
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
* 6.Метод замены переменной
1) ![]() . 2)
. 2) ![]() . 3)
. 3) ![]() . 4)
. 4) ![]() .
.
**7 Уравнения с параметром
1) ![]()
![]()
![]() . 2)
. 2) ![]() . 3)
. 3) ![]()
![]()
![]() . 4)
. 4) ![]()
![]()
![]()
**8 Уравнения
1) ![]() . 2) x2 = −9; q = 27. 3) P = ± 2. 4)
. 2) x2 = −9; q = 27. 3) P = ± 2. 4) ![]() .
.
.
Приложение.
Контроль знаний.
Уравнения Обязательный уровень.
№
п/п
Фамилия
имя
№ зад.
№ К.
1
2
3
4
5
6
7
8
Контроль знаний.
Уравнения Повышенный уровень.
№
п/п
Фамилия
имя
№ зад.
№ К.
1
2
3
4
5
6
7
8