Конспект урока Решение задач на применение аксиом стереометрии и их следствий

Урок 4. Решение задач на применение аксиом стереометрии и их следствий

Цель урока:

- сформировать навык применения аксиом стереометрии и их следствий при решении задач.

</ Ход урока

1. Организационный момент

2. Проверка домашнего задания

Двое учащихся у доски, один готовит решение задачи из домашней работы, другой доказательство одного из следствий из аксиом на выбор.

Остальные отвечают на вопросы математического диктанта.

Вариант I

1. Как называется раздел геометрии, изучающий фигуры в пространстве? (Стереометрия.)

2. Назовите основные фигуры в пространстве.

3. Сформулируйте аксиому А₂ .

4. Сформулируйте аксиому A₃.

5. Могут ли прямая и плоскость иметь только две общие точки? (Нет.)

6. Сколько плоскостей можно провести через три точки, не лежащие на одной прямой? (Одну.)

Вариант II

1. Как называется раздел геометрии, изучающий фигуры на плоскости? (Планиметрия.)

2. Назовите основные фигуры на плоскости.

3. Сформулируйте аксиому А₁.

4. Сколько плоскостей можно провести через прямую и не лежащую на ней точку? (Одну.)

5. Сколько может быть общих точек у прямой и плоскости? (Одна; бесконечно много; ни одной.)

6. Могут ли прямая и плоскость иметь только одну общую точку? (Да.)

Собрать листочки с ответами. Заслушать решение задачи и доказательство теоремы у доски.

3. Решение задач (фронтальная работа)

1. Назовите прямую, по которой пересекаются плоскости: а) МАВ и MFС, б) MCF и АВС.

2. Найдите длину CF и S_ABС.

3. Как построить точку пересечения прямой ДЕ с плоскостью АВС?

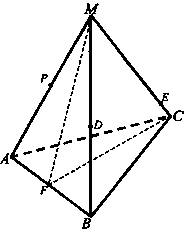
Решение:

М ∊ МАВ, М ∊ MFC,

1. а) => аксиома А₃ МАВ ∩ MFC = MF.

F ∊ МАВ и F ∊ MFC

C∊MCF, C∊ABC,

б) => аксиома А₃ MCF ∩ АВС = FC.

F ∊ MFC и F ∊ АВС

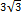
2. ΔАВС - равносторонний => FC - медиана, высота, биссектриса. ΔCFB - прямоугольный: СВ = 6 (см), FB = 3 (см). По теореме Пифагора FC = 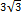(см). Sabc = АВ • CF; Sabc= 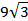(см²).

• Как еще можно найти длину FC?

• Как по-другому найти S_ABC?

3. DЕ и ВС лежат в плоскости ВМС. Пусть они пересекаются в точке К, так как К принадлежит ВС, значит К принадлежит плоскости АВС (аксиома А₂):

1 )DЕ ∊ ВМС, ВС ∊ ВМС;

2)DЕ ∩ ВС = К (К ∊ ВС => К ∊ АВС).

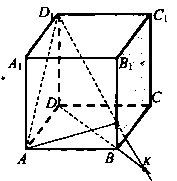
Задача № 2Дан куб АВСDА₁В₁С_1D1, РЄВВ₁, В₁Р ⁼ РВ.

1. Как построить точку пересечения плоскости АВС с прямой D₁Р?

2. Как построить линию пересечения плоскости АD₁Р и АВВ₁ ?

3. Вычислите длину отрезков АР и АD₁, если АВ = а.

Решение:

1. D₁Р и DВ лежат в одной плоскости Д₁ДВ. Пусть они пересекаются в точке К. Тогда точка К принадлежит прямой DВ, а значит, К Є АВС.

2. Точка Р принадлежит ВВ₁, а значит, и плоскости АВВ₁. Точка Р принадлежит АВ, а значит, и плоскости АВВ₁. Следовательно, по аксиоме А₂: АР с АВВ₁. Аналогично АР с АD₁Р. Значит, АD₁Р∩ АВВ₁ =АР.

а) Из ΔАВР, по теореме Пифагора АР =

б) Из ΔАDD₁ по теореме Пифагора АD₁ = а .

Далее работа строится следующим образом:

I уровень (задачи № 3, 4- фронтальная работа)

II уровень (самостоятельная работа)

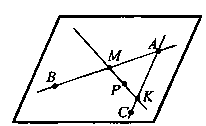
Задача N 3Точки А, В, С не лежат на одной прямой. МЄАВ,КЄАС,РЄМК.Докажите, что точка Р лежит в плоскости АВС.

Решение:

АВ ∩ АС=А. По второму следствию прямые АВ и АС определяют плоскость ά. Точка М Є АВ, а значит, принадлежит плоскости ά, и точка К Є АС, а значит, и плоскости ά . По аксиоме А₂: MKc ά. Точка Р Є МК, а значит, и плоскости ά .

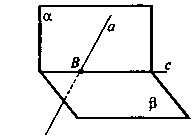
Задача № 4Плоскость ά и β пересекаются по прямой с. Прямая а лежит в плоскости ά и пересекает плоскость β. Пересекаются ли прямые a ис? Почему?

Решение:

По условию, прямая а пересекает плоскость β. Пусть a ∩ β = В(ВЄ а). По условию прямая а принадлежит плоскости ά, значит,

В Є ά. По аксиоме А₃ существует прямая с, такая, что ВЄс.

II уровень (самостоятельное решение задач)

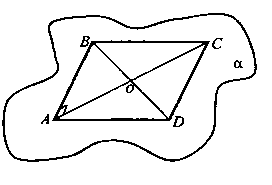
1. Дан прямоугольник АВСД, О - точка пересечения его диагоналей. Известно, что точки А, В, О лежат в плоскости ά. Докажите, что точки С и Д также лежат в плоскости ά. Вычислите площадь прямоугольника, если АС =8 (см), <AOB = 60°.

1) Так как В принадлежит ά и точка О принадлежит ά, то ВО принадлежит ά. Так как точка Д принадлежит ВО, то Д принадлежит ά (по аксиоме А₂). Аналогично точка С принадлежит ά:

1. В Є ά, О Є ά => ВО с ά;

2. Д Є ВО =>ДЄ ά (акс. А₂);

3. А Є ά, О Є ά => АО c ά ;

4. СЄАО => С Є ά (акс. А₂).

2) Возможны различные способы решения задачи:

1. Найти стороны прямоугольника.

2. Использовать тот известный факт, что диагонали параллелограмма (прямоугольника) разбивают его на четыре равновеликих треугольника, и найти сначала площадь одного из треугольников.

3. Использовать формулу S =d₁ d₁ sinά.

(Ответ: 16 см².)

4. Подведение итогов

Оценки за урок.

Домашнее задание пп. 1-3 учить

Домашнее задание

1. Точки А, В, С не лежат на одной прямой. МЄАВ,КЄАС,РЄМК.Докажите, что точка Р лежит в плоскости АВС.

2. Плоскость ά и β пересекаются по прямой с. Прямая а лежит в плоскости ά и пересекает плоскость β. Пересекаются ли прямые a ис? Почему?

Домашнее задание

1. Точки А, В, С не лежат на одной прямой. МЄАВ,КЄАС,РЄМК.Докажите, что точка Р лежит в плоскости АВС.

2. Плоскость ά и β пересекаются по прямой с. Прямая а лежит в плоскости ά и пересекает плоскость β. Пересекаются ли прямые a ис? Почему?

Домашнее задание

1. Точки А, В, С не лежат на одной прямой. МЄАВ,КЄАС,РЄМК.Докажите, что точка Р лежит в плоскости АВС.

2. Плоскость ά и β пересекаются по прямой с. Прямая а лежит в плоскости ά и пересекает плоскость β. Пересекаются ли прямые a ис? Почему?

Домашнее задание

1. Точки А, В, С не лежат на одной прямой. МЄАВ,КЄАС,РЄМК.Докажите, что точка Р лежит в плоскости АВС.

2. Плоскость ά и β пересекаются по прямой с. Прямая а лежит в плоскости ά и пересекает плоскость β. Пересекаются ли прямые a ис? Почему?

Домашнее задание

1. Точки А, В, С не лежат на одной прямой. МЄАВ,КЄАС,РЄМК.Докажите, что точка Р лежит в плоскости АВС.

2. Плоскость ά и β пересекаются по прямой с. Прямая а лежит в плоскости ά и пересекает плоскость β. Пересекаются ли прямые a ис? Почему?

Домашнее задание

1. Точки А, В, С не лежат на одной прямой. МЄАВ,КЄАС,РЄМК.Докажите, что точка Р лежит в плоскости АВС.

2. Плоскость ά и β пересекаются по прямой с. Прямая а лежит в плоскости ά и пересекает плоскость β. Пересекаются ли прямые a ис? Почему?

Домашнее задание

1. Точки А, В, С не лежат на одной прямой. МЄАВ,КЄАС,РЄМК.Докажите, что точка Р лежит в плоскости АВС.

2. Плоскость ά и β пересекаются по прямой с. Прямая а лежит в плоскости ά и пересекает плоскость β. Пересекаются ли прямые a ис? Почему?

Домашнее задание

1. Точки А, В, С не лежат на одной прямой. МЄАВ,КЄАС,РЄМК.Докажите, что точка Р лежит в плоскости АВС.

2. Плоскость ά и β пересекаются по прямой с. Прямая а лежит в плоскости ά и пересекает плоскость β. Пересекаются ли прямые a ис? Почему?

Домашнее задание

1. Точки А, В, С не лежат на одной прямой. МЄАВ,КЄАС,РЄМК.Докажите, что точка Р лежит в плоскости АВС.

2. Плоскость ά и β пересекаются по прямой с. Прямая а лежит в плоскости ά и пересекает плоскость β. Пересекаются ли прямые a ис? Почему?