Урок по теме Производная

Муниципальное казенное общеобразовательное учреждение «СОШ №2»

Урок - семинар

по теме

«Производная. Правила вычисления производных».

10 класс

Учитель Щербакова Н.М.

2015 год

Урок - семинар по теме

«Производная. Правила вычисления производных».

Цель урока:

Обобщение знаний учащихся по данной теме, систематизация умений и навыков, проверка правильности использования математических символов.

План урока:

(для предварительного ознакомления учащимися)

1.Теоретические вопросы по теме

-определение производной;

-геометрический и физический смысл производной;

-правила вычисления производных функций;

-элементарные функции и их графики.

2. Подготовить историческую справку о возникновении понятия «производная».

3. Практическая часть на выполнение заданий по вычислению производных заданных функций.

Эпиграф к уроку:

«Природа формулирует свои законы языком математики»

Г.Галилей

Ход урока:

1.Экскурсия в историю дифференциального исчисления.

( историческая справка)

«История математики в школе 9-10 классы», Г.И. Глейзер.

2.Устный опрос учащихся на знание теории и основных формул дифференцирования.

- определение производной;

-геометрический и физический смысл производной;

- основные формулы дифференцирования: производная суммы, произведения, частного, производная синуса, косинуса, сложной функции, частные формулы, правила дифференцирования.

3. Игра - соревнование «Найди себе пару»

Задание:

Выписать пары «функция» - «производная». На столах учащихся раздаточный материал в виде таблицы.

x⁵

¹

x

2

2x

3

1

4

2

5

x ^-3

⁶

7

sin x

8

5x⁴

⁹

-3x ^-4

¹⁰

x²

¹¹

-3

12

-sin x

13

-2/x³

¹⁴

ax

15

a

16

cos x

17

1/(2)

18

0

19

12x ^-5

²⁰

Проверить устно правильность выполнения задания. Например,

1-9,2-4,3-5,15-16,7-18,8-17,17-13,10-20,4-19,5-19,6-10,12-19,

16-19,11-2.

4.Устная работа на нахождение производных функций.

(см. приложение 1)

5. Опрос учащихся у доски.

Найти производные функций:

1) у=2х²+3х 1)у=3х⁴

2)у=2х³ 2)у=5х⁵+4х³-х²+2х-5

3)у=7х^-2 3)у =х ^-6

4)у = 4)у =

5)у =7(5х² -3)⁴ 5)у=-11(3-8х³)⁵

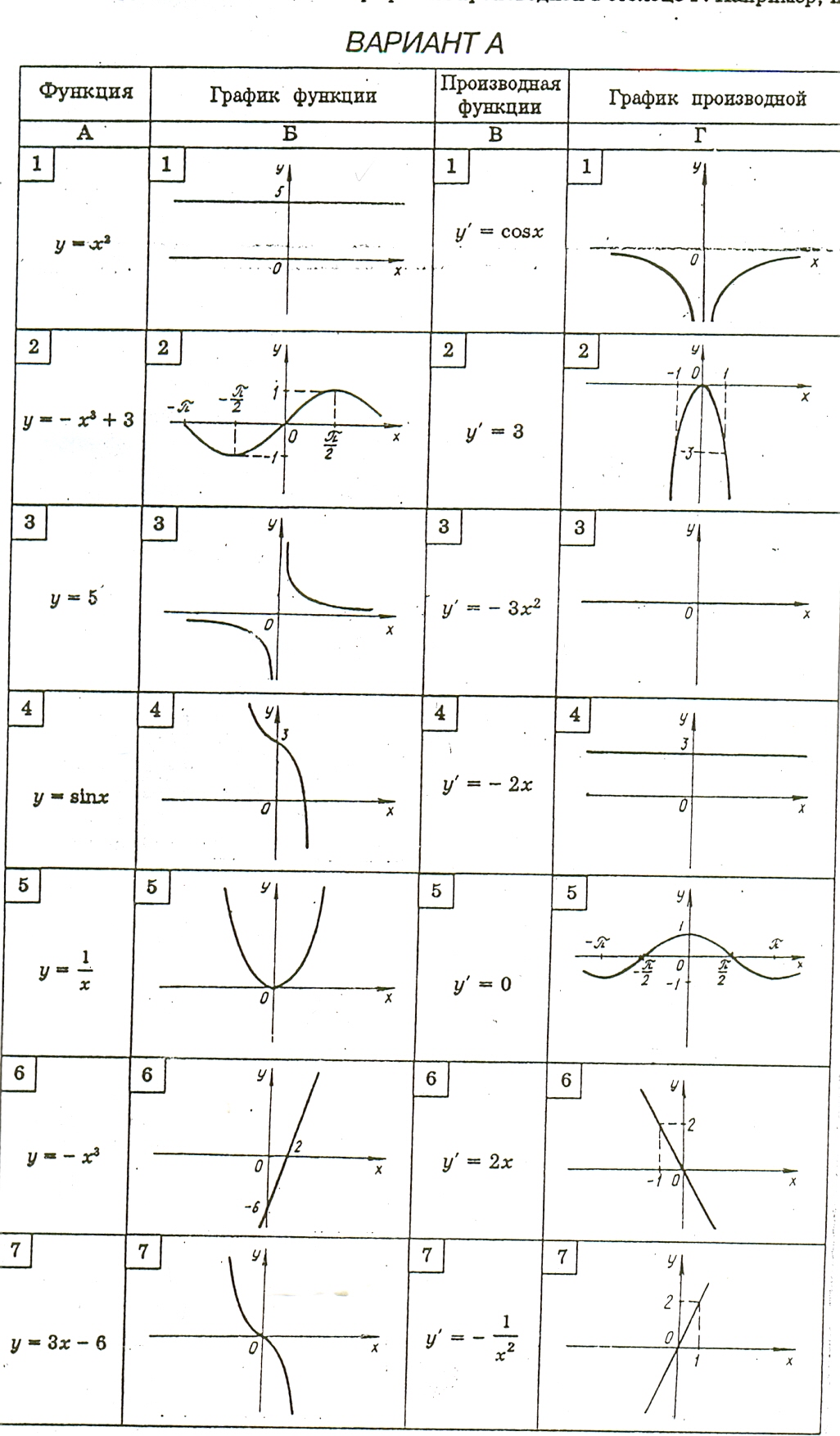
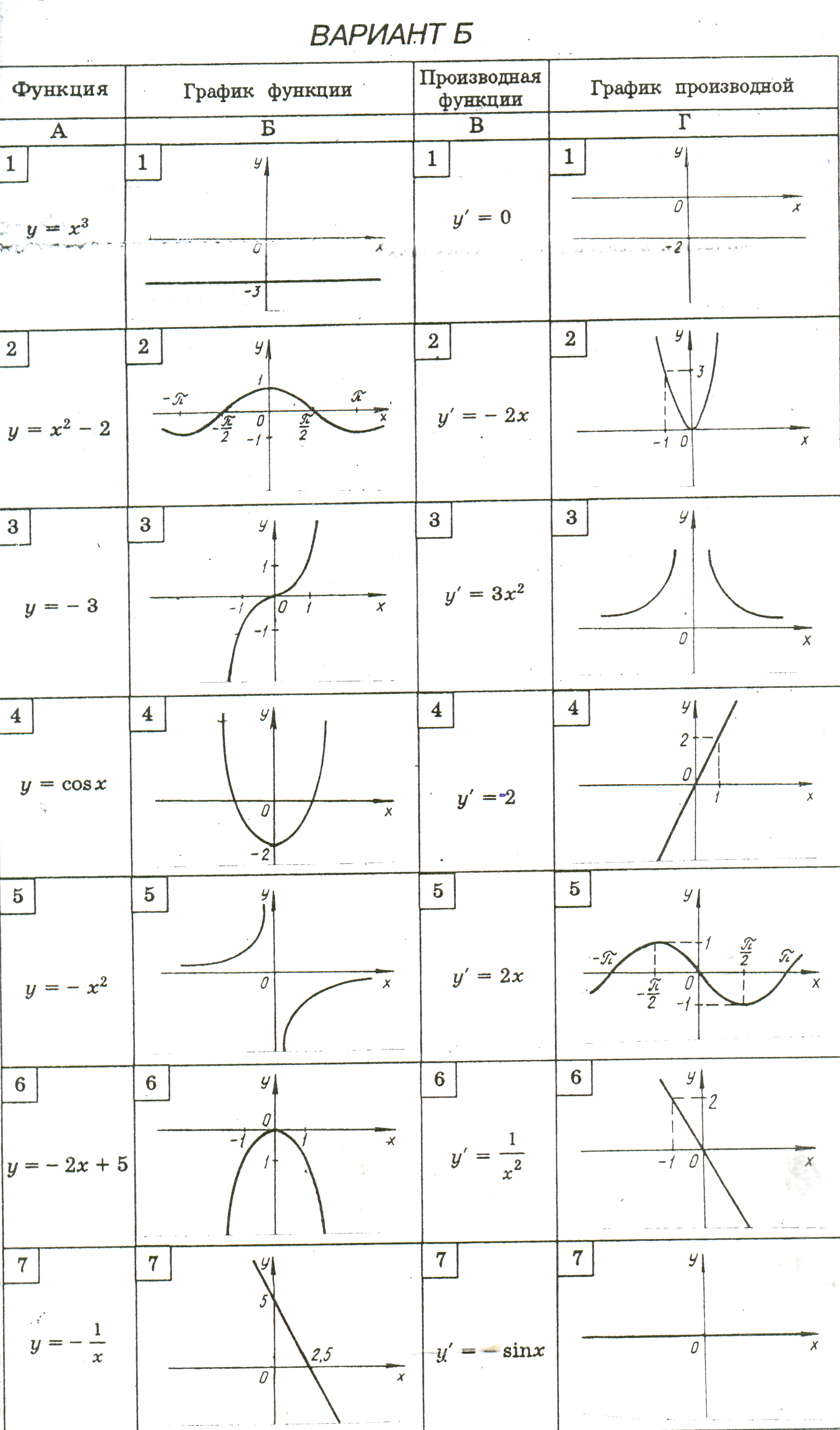
6. «Задачи-картинки». Установите соответствие между функцией, записанной в столбце «А», ее схематическим графиком, изображенным в столбце «Б», производной функции в столбце «В» и графиком производной в столбце «Г».

(Проверка на закрытой доске)

(Приложение 2)

Вариант «А» Вариант «Б»

7. 1-3-3-2

   2. 2-4-5-4

3. 1. 5. 3. 3-1-1-7

4. 2. 1. 5. 4-2-7-5

5. 3. 7. 1. 5-6-2-6

6. 7. 3. 2. 6-7-4-1

7. 6. 2. 4. 7-5-6-3

7.Самостоятельная работа по вариантам.

1 вариант 2 вариант

1.Найдите производную функции:

a) f(x) =x² - 2; a)f(x)=2 x² - 4;

б)f(x) = cos 5x - tgx б)f(x) =sin 7x +3ctgx

2.Вычислите значение производной функции в точках:

f(x) = 3x-4x³ f(x) =-2x²+x⁴

x₀=1; x₀=-5 x₀=2; x₀=-

3.Решите неравенство:

f′ (x) ≥ 0, если f(x)=6x-3x² f′ (x) < 0, если f(x)=-4x+2x²

8. Подведение итогов урока.

ПРИЛОЖЕНИЕ 1

Устные упражнения по теме:

«Правила нахождения производной»

Таблица 1

-5x² + 4x⁶)′

-10x + 24x⁵

x² + x

3x²

-17x²

-4x³

0,5x³

13x²+26

8x²-16

3x²-5x+6

5x²+6x-7

x⁴+2x²

2x¹¹+7x ^-5

x⁷ - x ^-13

8x ^-24 +36

-x¹²¹ - x⁷²

x¹¹ - 28x

13x¹⁵ + 10x ^-34 -25x-π

Таблица № 2

(2x - 3)²

(6x - 3)⁵

(x - 3)^-3

( - x⁴)²

(1 - 2x)⁴

(1 - 5x)⁵

(x + 1)²- 3x

(x - 3)⁷

(3x - 1)^-3

(3x + 2)^-4

(-4x + 6)³

(x⁵ + 5x)⁴

(5x³ + 7x² - x⁴)⁵

(2+x³ - x ^-2)⁷

Таблица № 3

cosx

-6sin 7x+5

-3cos5x+4

-8tg x

-3ctg x+x²

5cos 3x - 6

cos x-7

-8tg x+5

5cos x- x⁴

ctg 2x

-sin 3x

-4cos 2x

sin³ x

-cos⁴ x

tg³ 3x

Таблица № 4

функции в точке x₀

Пример: 2x²

x₀ = 3; f′(x) = 4x;

f′(3) = 4·3 =12

-8 x⁴

x₀ = - 2

11x² +x

x₀ = -1

8x⁵ - 3x

x₀ = 1

(2 -x)³

x₀ = 1

(7x -4)⁴

x₀ = 2

sin x

x₀ = π

-cos x

x₀ = π

3tg x

x₀ = 0

ctg x

x₀ = π

7x⁴-5sin3x

x₀ = 0

11x² - 5x³ + x

x₀ = - 1

π - 42cos x + 30sin x

x₀ = 3π

tg x - 3 sin x +185

x₀ = 2π

14x ^{- 2} +15x⁴ + x

x₀ = - 1

Приложение 1

8 класс.

Тема урока «Решение квадратных уравнений»

Цель урока: обобщение и систематизация знаний обучающихся по теме "Решение уравнений".

Форма работы: групповая, индивидуальная.

Подготовка к уроку: класс разбит на пять групп по 5 человек в каждой. У учеников в группе номера от 1 до 5. В группе выбирается консультант. Консультант оказывает помощь товарищам по группе, проверяет решения, выставляет оценки.

Оборудование: карточки с заданиями .

Ход урока:

1.Фронтальный теоретический опрос учащихся в группах.

Задания группам:

-Квадратное уравнение. Виды квадратных уравнений. Общий вид.

-Неполные квадратные уравнения. Способы их решения. Определение, общий вид.

-Приведенные квадратные уравнения. Способы их решения.

-Дискриминант квадратного уравнения. Сколько корней имеет квадратное уравнение?

-Сформулируйте теорему Виета. Чему равны сумма и произведение корней квадратного уравнения ах² +bx +c =0?

Проверка основных формул на доске.

Карточка №1:

1. Ответ: D=0, x=-1

2. ответ: D=49,

3. ответ: х=-3, 3

Карточка №2:

1. ответ: D=36, x=-5, 1

2. ответ: D=0, x=0,5

3. ответ: х=0, 7

Карточка №3:

1. ответ х=0, 2

2. ответ х=-4, 4

3. ответ D=9, x=-3, -6

Карточка №4:

1. ответ D=4, x=1, 3

2. ответ D=16, x=3, -1

Карточка №5:

1. ответ D=4, x=4, 2

2. ответ D=4, x=-1, -3

Сгруппировать уравнения по какому-либо признаку.

х²+2х-9=0 7х²-14х=0

х²-7х=0 3х²-2х+19=0

х²-3х+1=0 16х²=0

х²-9=0 х²-19х+48=0

7х-х²=4 5х²=6х

ГРУППЫ УРАВНЕНИЙ

полные неполные

х²+2х-9=0 7х²-14х=0

3х²-2х+19=0 х²-7х=0

х²-3х+1=0 16х²=0

х²-19х+48=0 х²-9=0 7х-х²=4 5х²=6х

Самостоятельная работа по теме «Квадратные уравнения»

Вариант А1 Вариант А2

1.Решить уравнения:

а) x²-5x+6=0 a) x^2-7x+10=0

б)y²+8y+16=0 б) y²-10y+25=0

в)-t²-3t+1=0 в)-t²+t+3=0

г)3a²+a=7 г)2a²-a=3

2.При каких значениях х равны значения многочленов:

(х+1) ² и 7х-3х²? (х-1) ² и 2х-2х²?

Вариант Б1 Вариант Б2

1.Решить уравнения:

а)х² +7х-44=0 а)х² -10х-39=0

б)9у² +6у-44=0 б)4у² -4у+1=0

в)-2t² +8t+2=0 в)-3t² -12t+6=0

г)а² +3а=-11 г)4а² +5=а

2.При каких значениях х равны значения многочленов:

(2-х)(2х+1) и (х-2)(х+2)? (1-3х)(х+1) и (х+1)(х-1)?

Вариант В1 Вариант В2

1.Решить уравнения:

а)х² +х-72=0 а)х² -5х-84=0

б)2у² -2у+0,5=0 б)8у² +4у+0,5=0

в)-15=3t(2-t) в)10t=5(t² -4)

г)а=а² +4 г)а=а² +1

2.При каких значениях х равны значения многочленов:

х² - 1,5х - 0,5 и х-1? х² -х- и 2х+4?

ТРЕНАЖЕРЫ УСТНОГО СЧЕТА

ПО ТЕМЕ

1.ПРАВИЛА НАХОЖДЕНИЯ ПРОИЗВОДНОЙ

2.СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ