Исследование уравнений с параметрами 11 класс

Тема: Исследование уравнений с параметрами

Цель: продолжить формулировать умение решать уравнения, содержащие параметры

Тип: урок новых знаний

Ход урока:

1. Вводное слово

Задачи с параметрами отличаются особенным разнообразием и нестандартностью. Не случайно без них, как правило, не обходиться Олимпиады всех уравнений, вступительные экзамены в наиболее престижные вузы.

Задания, которые мы разберём сегодня на уроке представляют собой наиболее распространённые виды задач с параметрами, которые удобно решаются графически. Это примеры повышенной сложности. Они требуют глубокого анализа условия. Прежде всего следует вспомнить, что существует два основных способа решения уравнений с параметрами: графический и аналитический.

Графический способ: применяется тогда, когда параметр присутствует в уравнение только в качестве слагаемого и не связок с переменной. В этом случае приём решения состоит из следующих действий.

1. Уединить параметр в оду из частей уравнения

2. Решить полученное уравнение графически

3. Найти(по графику) значения параметра, удовлетворяющие условию задачи

Аналитический способ: это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Иногда говорят, что это способ силового, в хорошем смысле «наглого» решения. По мнению специалистов аналогичный способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности.

2. Начнём с тренировочных упражнений:

1)Установить соответствие между чертежами на доске и…

y=x-2

y=Ix-2I

y=IxI-2

IyI=x-2

y=IIxII-2I

Заполните таблицу и сдайте учителю

а

б

в

г

1

2

3

4

5

2)Остановимся на построение графика y=IIxI-2I

Какие этапы мы должны пройти при построении данного графика функции

3)Постройте график функции

Y=IIxI-2I

4)Сколько корней имеет уравнение IIxI-2I-a=0

при различных значениях параметра а?

1. y=IIxI-2I

y=a

Ответ:(требуется глубокий анализ условий)

a<0

а=0

0

a´=2

a>2

3. Составить алгоритм:

4. Решить уравнение и найти решение для каждого а

Ix-1I+Ix-3I=a

Ответ: a<2

a=2

a>2

5. Найти все значения а при которых уравнение

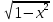=а-x имеет единое решение

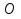твет: a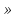[-1;1)U{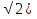

6. При каких значениях

1. K уравнение

Ix²-6*IxI+8I=K

Ответ: k=0; x=-4;-2;2;4

1<k<8;

2)

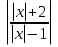=k

Ответ: 1

7. Закончите фразу

1. Существует аналитический метод решения уравнений с параметром и…

2. Графический удобно применить, если параметр присутствует в уравнение, как слагаемое и не зависит от…

3. При решении графическим методом первое, что мы должны сделать, это…

4. Второе…

5. Третье…

6. Вы сегодня работали….