Урок по теме Площадь криволинейной трапеции

Конспект открытого урока

По теме:

Площадь криволинейной трапеции

Цель урока - закрепить навыки нахождения определенного интеграла, обеспечить усвоение студентами понятия «криволинейная трапеция» и различных способов нахождения площади криволинейной трапеции, отработать навыки нахождения площади криволинейной трапеции путем вычитания площадей.

Задачи урока:

Образовательная -формирование умений нахождения площади,

Развивающая - развитие психических качеств студентов (умений применять полученные знания на практике); развитие познавательных умений и мышления (выделять главное, анализировать, сравнивать, определять и объяснять понятия).

Воспитательная - активизировать интерес к получению новых знаний, воспитание положительного отношения к знаниям, дисциплинированности;

Тип урока: комбинированный.

Оснащение:

- мультимедийный проектор, экран;

- операционная система Microsoft Office 2003/2007: PowerPoint, Word, Excel;

- Колмогоров А.Н. и др Алгебра и начала анализа . Учебник для 0-11классов общеобразовательных учреждений, М.:Просвещение.2000

- карточки-задания.

- презентация PowerPoint;

- ЭОР.

1.Самоопределение к деятельности

(оргмомент)

Проверяет готовность обучающихся к уроку; отмечает отсутствующих;

формулирует тему и цели урока

Готовятся к восприятию материала

На экране тема, цель

2. Актуализация опорных знаний

Обеспечивает повторение знаний и умений, полученных на предыдущих уроках:

тест (часть класса) - вопросы прилагаются;

Вопросы:

Сформулируйте формулу Ньютона-Лейбница.

Вычислите интеграл

Историческая справка.

Проходят тестирование

фронтальный опрос с решением примеров.

Решают примеры.

Историческая справка (задание с прошлого урока).

задание на экране 1. ехе

слайд 1

3. «Открытие» новых знаний

Формулирует тему урока

Записывают тему урока в тетрадях.

слайд 2

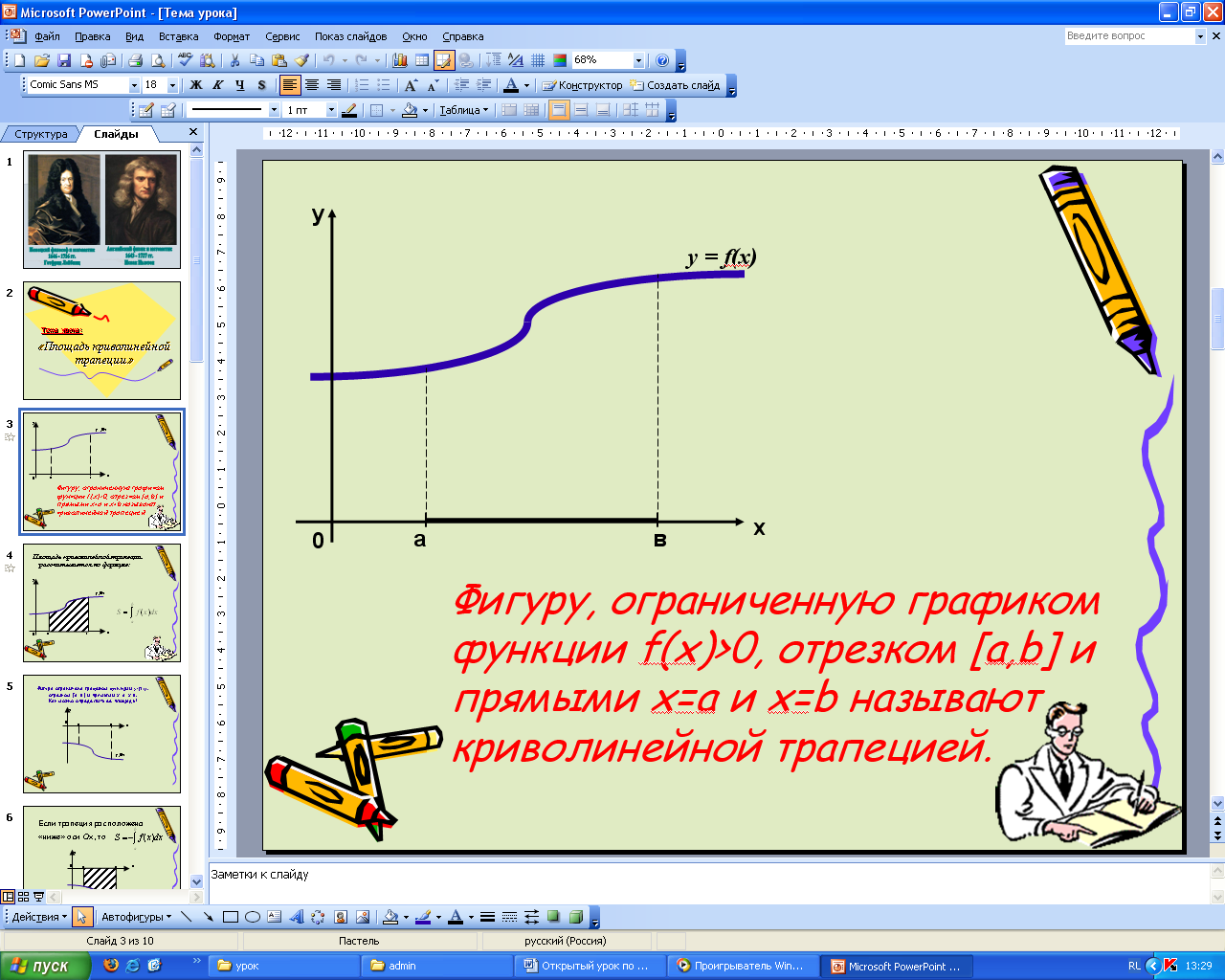
Формулирует определение криволинейной трапеции

Делают чертеж и записывают определение в тетрадях.

слайд 3

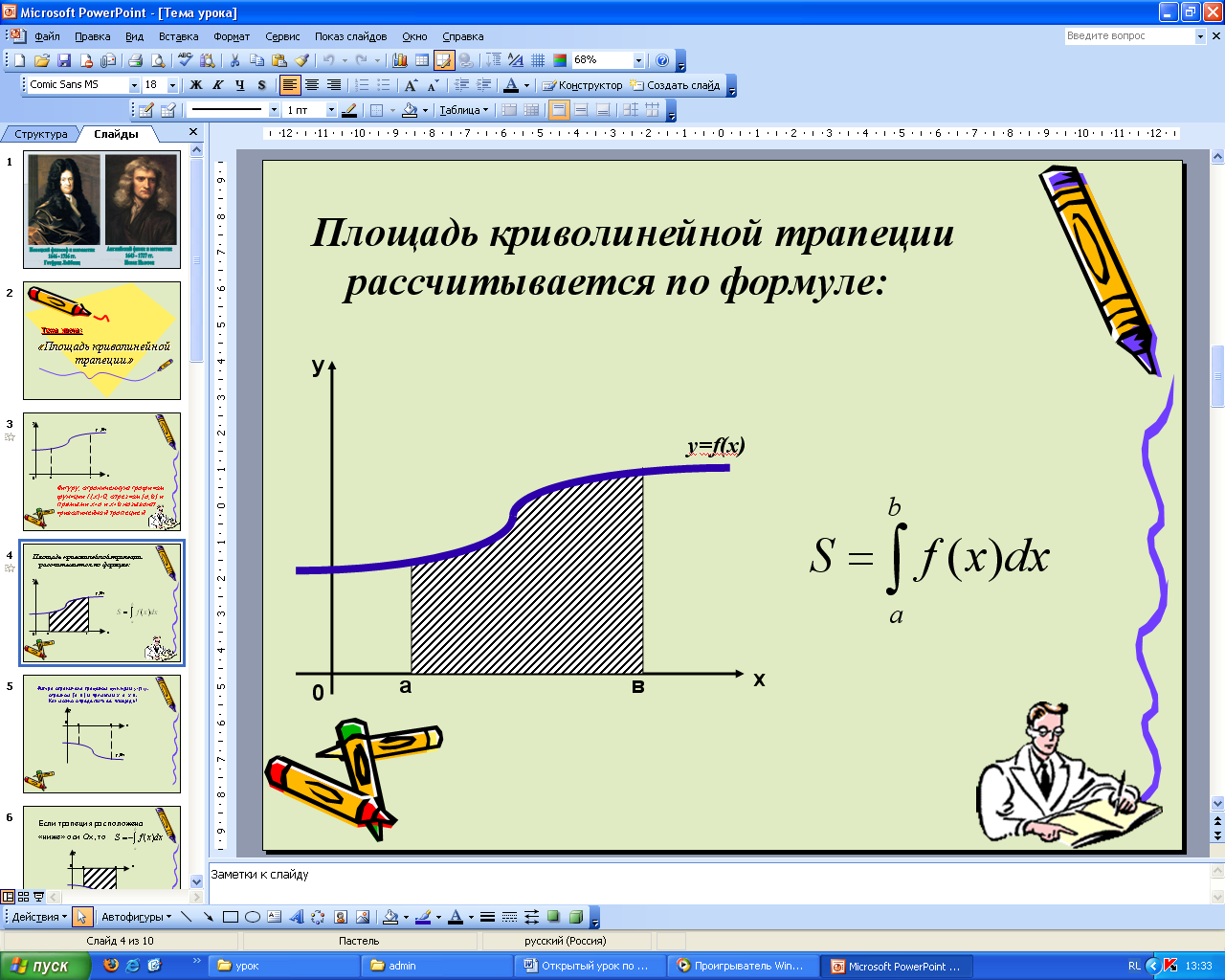
Записывает формулу площади криволинейной трапеции

Приводит способы нахождения площадей различных фигур

Записывают формулу в тетрадях.

Отвечают на поставленные вопросы.

Записывают в тетрадях.

слайд4

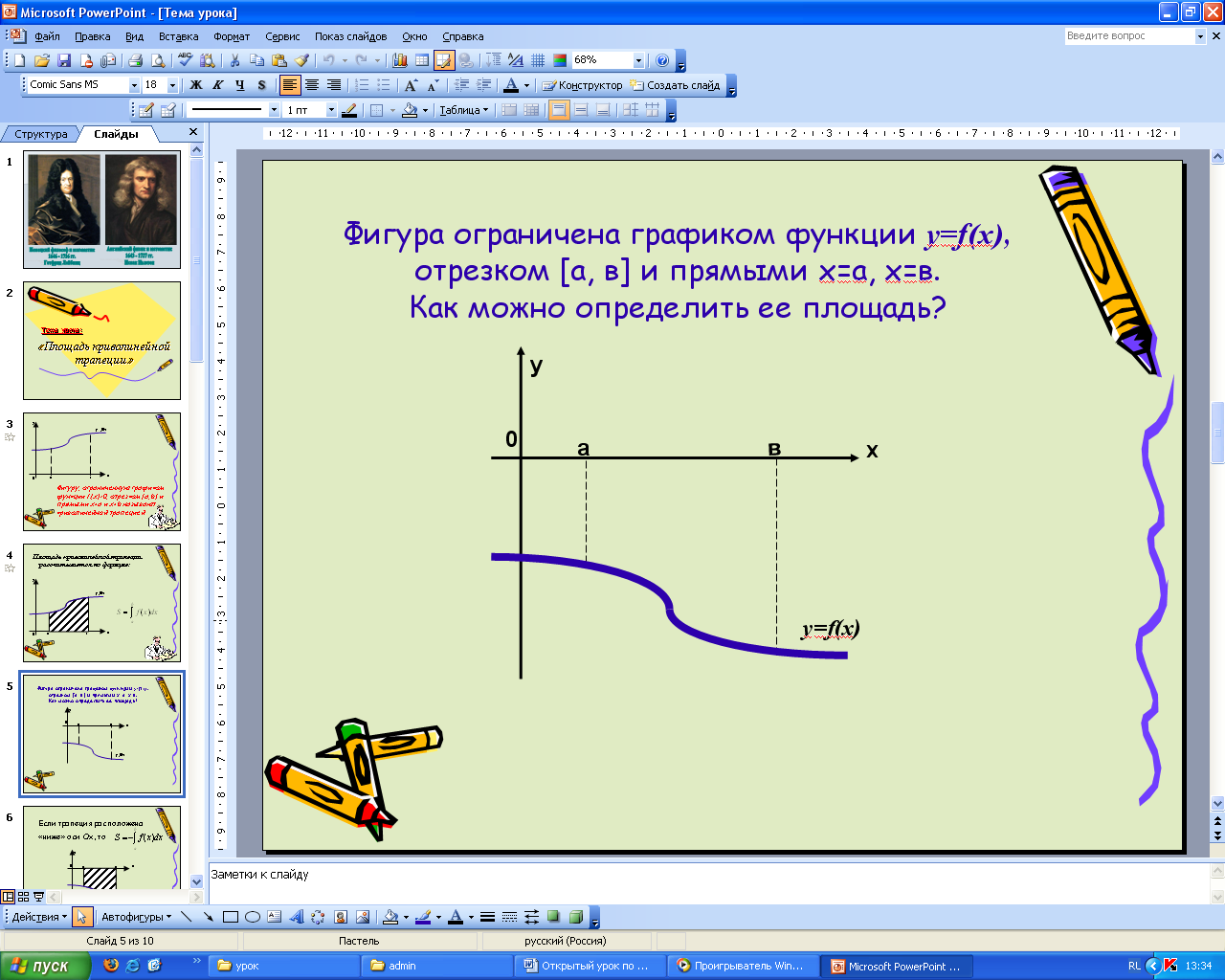
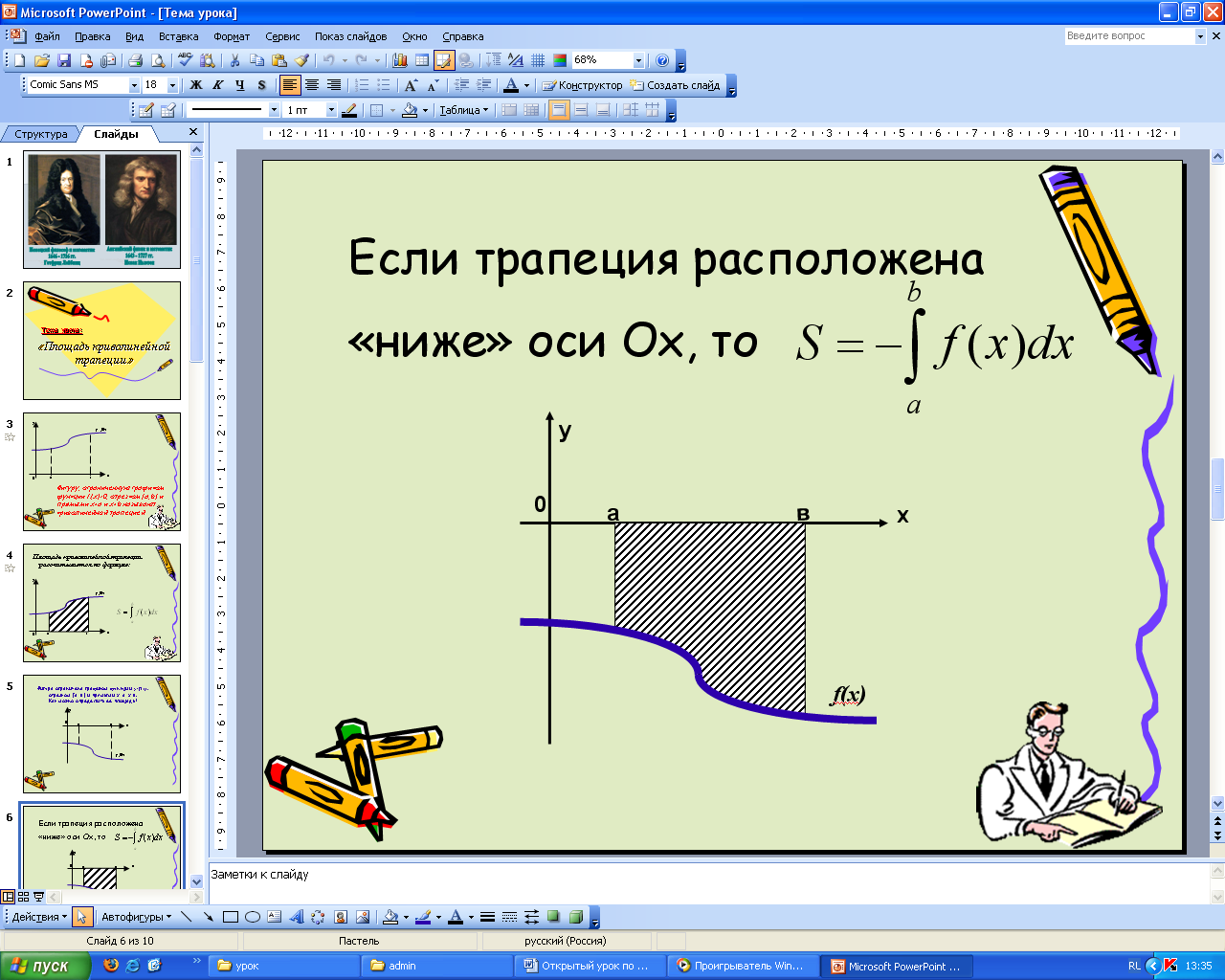
слайды 5,6,7.8,9,10

4. Применение знаний, формирование умений

Решает пример ЭОР

Записывают решение в тетрадях.

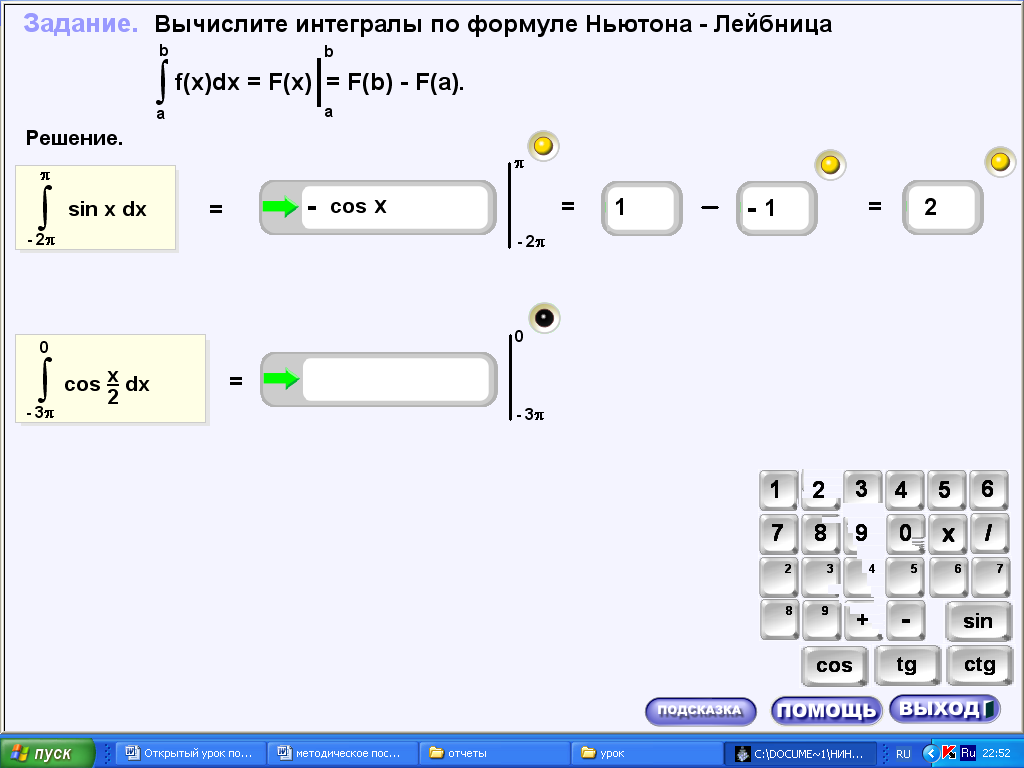
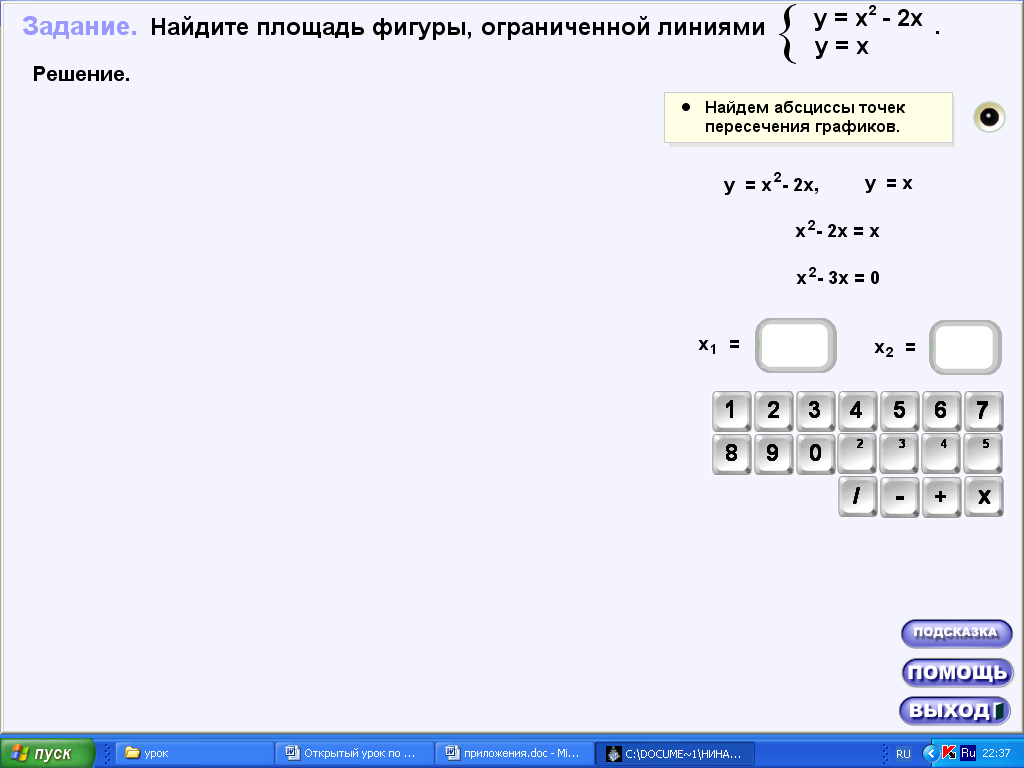
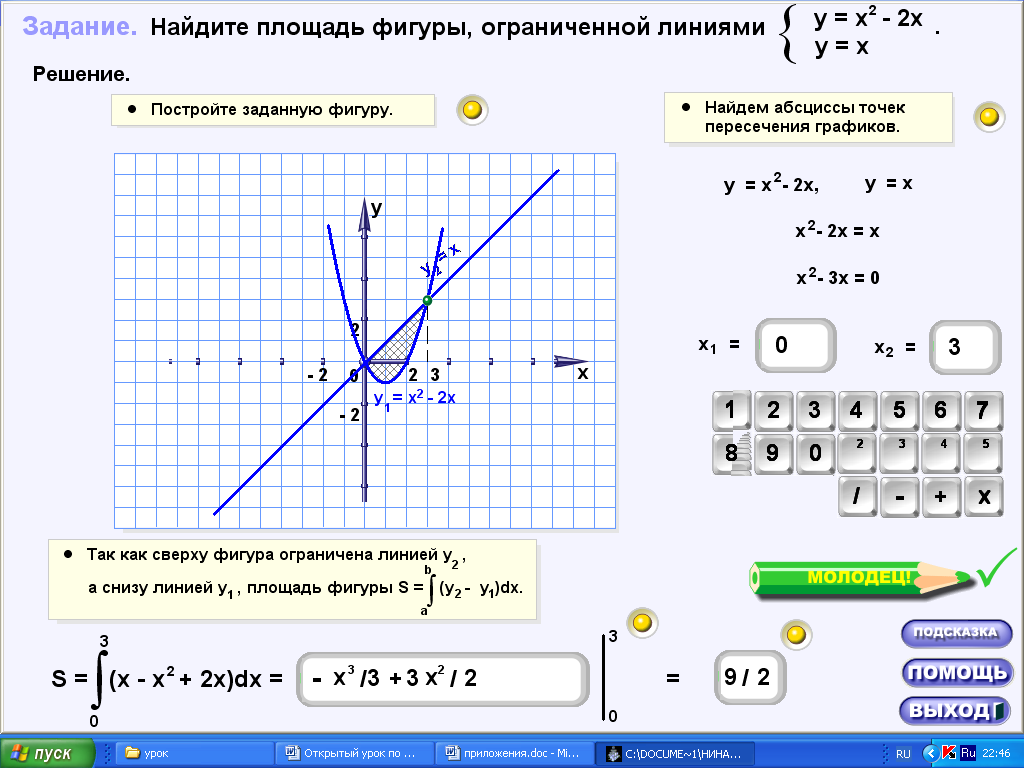
2.ехе, практика, задача 2

Руководит решением примеров на ИД

Решают примеры и записывают их в тетрадях.

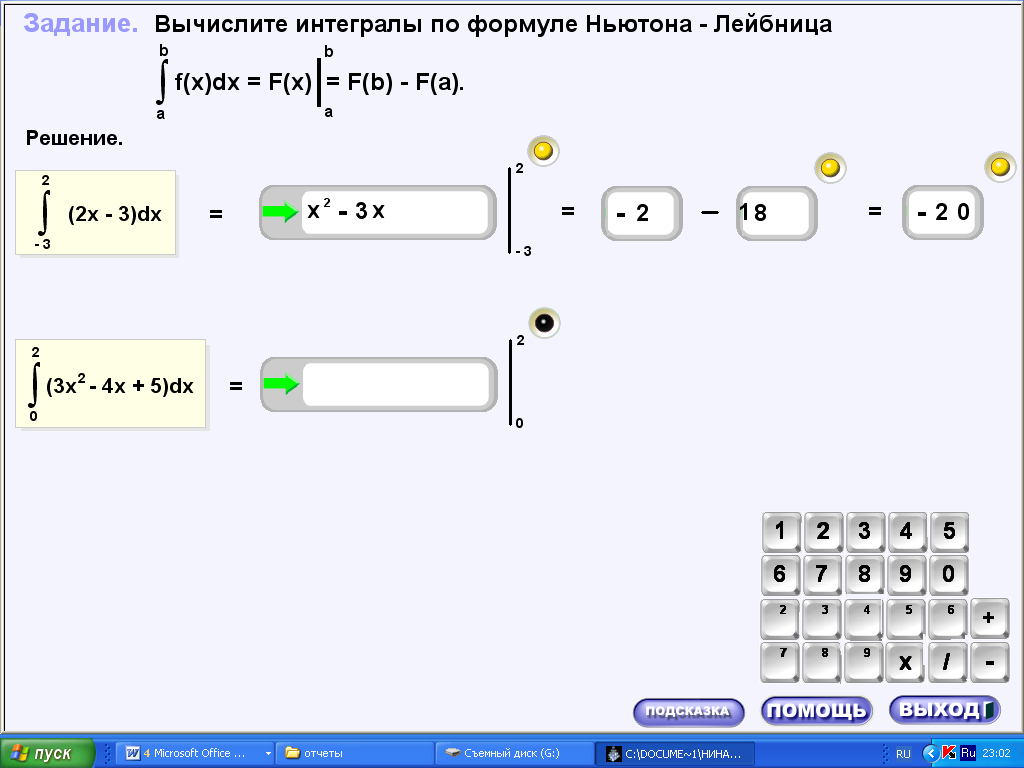
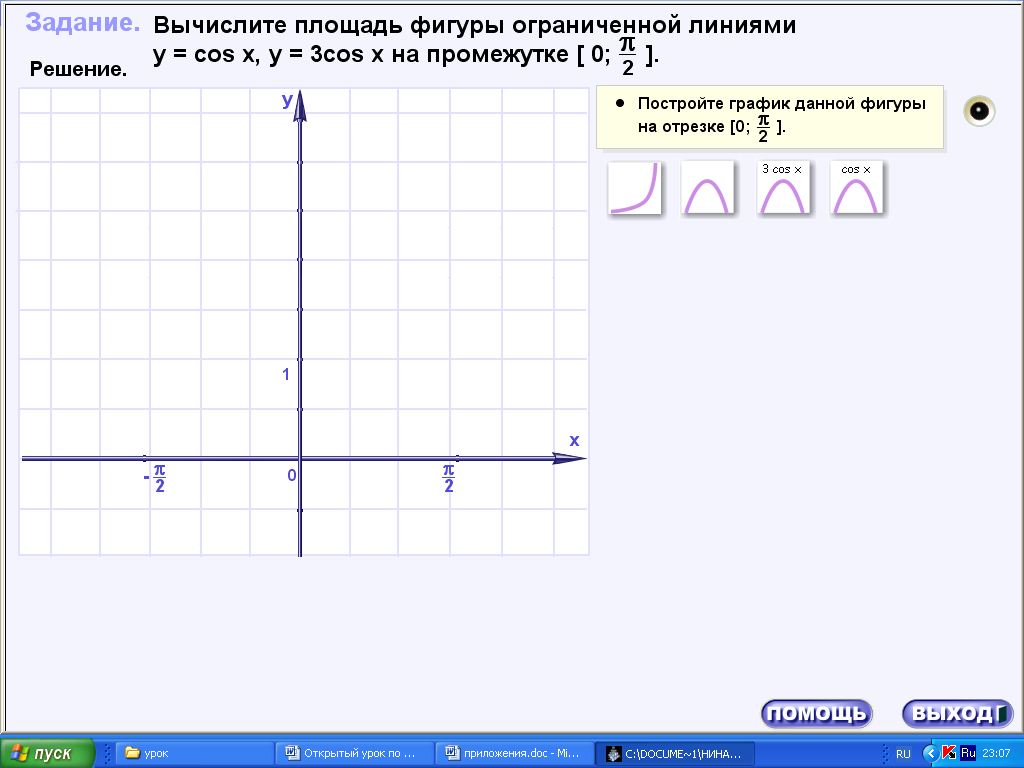
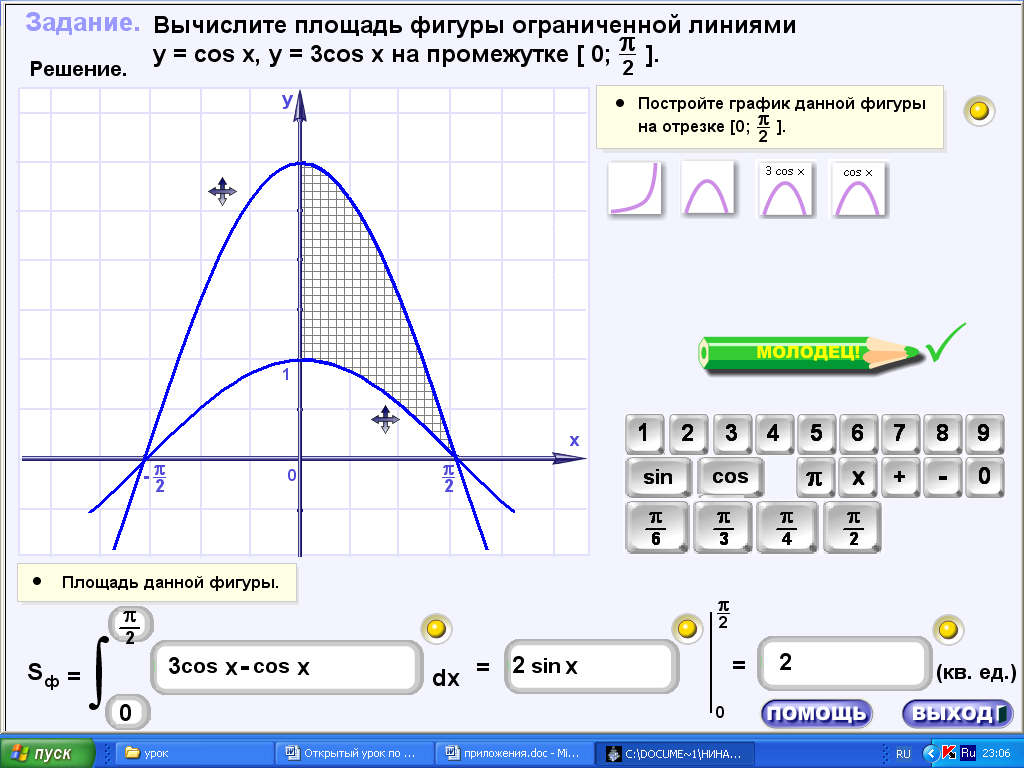
15.ехе. практика, задача1

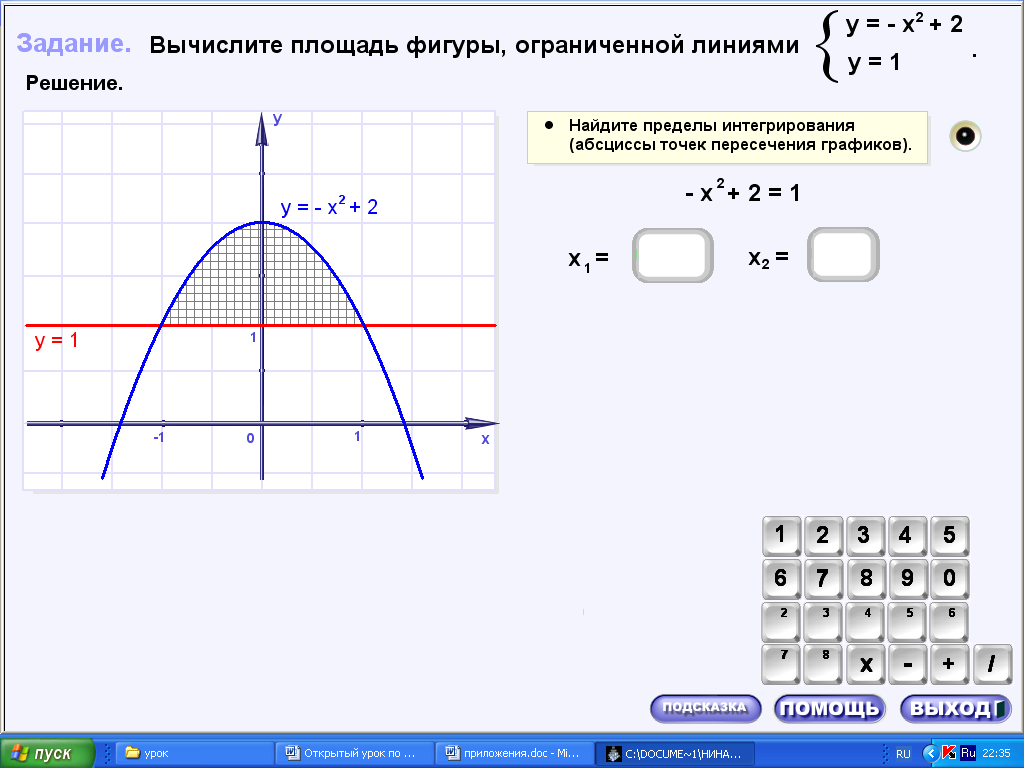
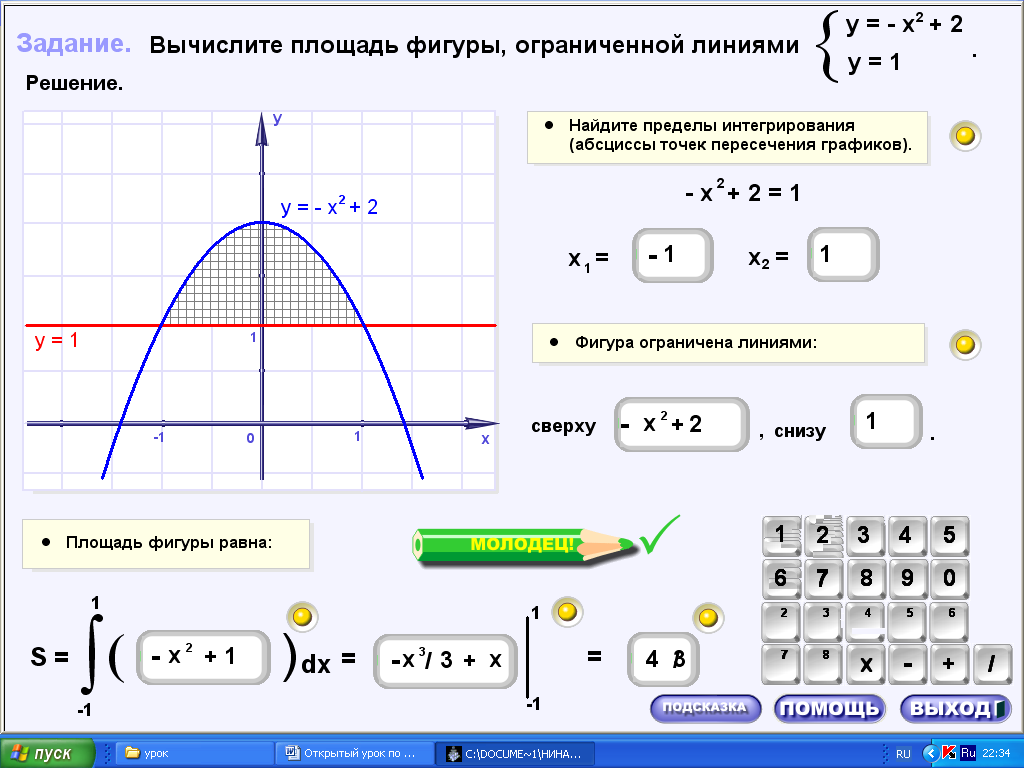
3.ехе, задача 3

Контролирует написание самостоятельной работы.

На выданных листах решают дифференцированную самостоятельную работу.

5. Рефлексия

Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.

Отвечают на вопрос

6. Подведение итогов.

Д/задание.

Выставление оценок.

Домашнее задание -вычислить площади фигур ограниченных линиями

Дополнительное задание:

Найти в Интернет примеры практического применения вычисления площади криволинейной трапеции.

Записывают домашнее задание в тетрадях.

Приложение 1

Вопросы тестового контроля

1. Чему равен нижний предел интегрирования в интеграле

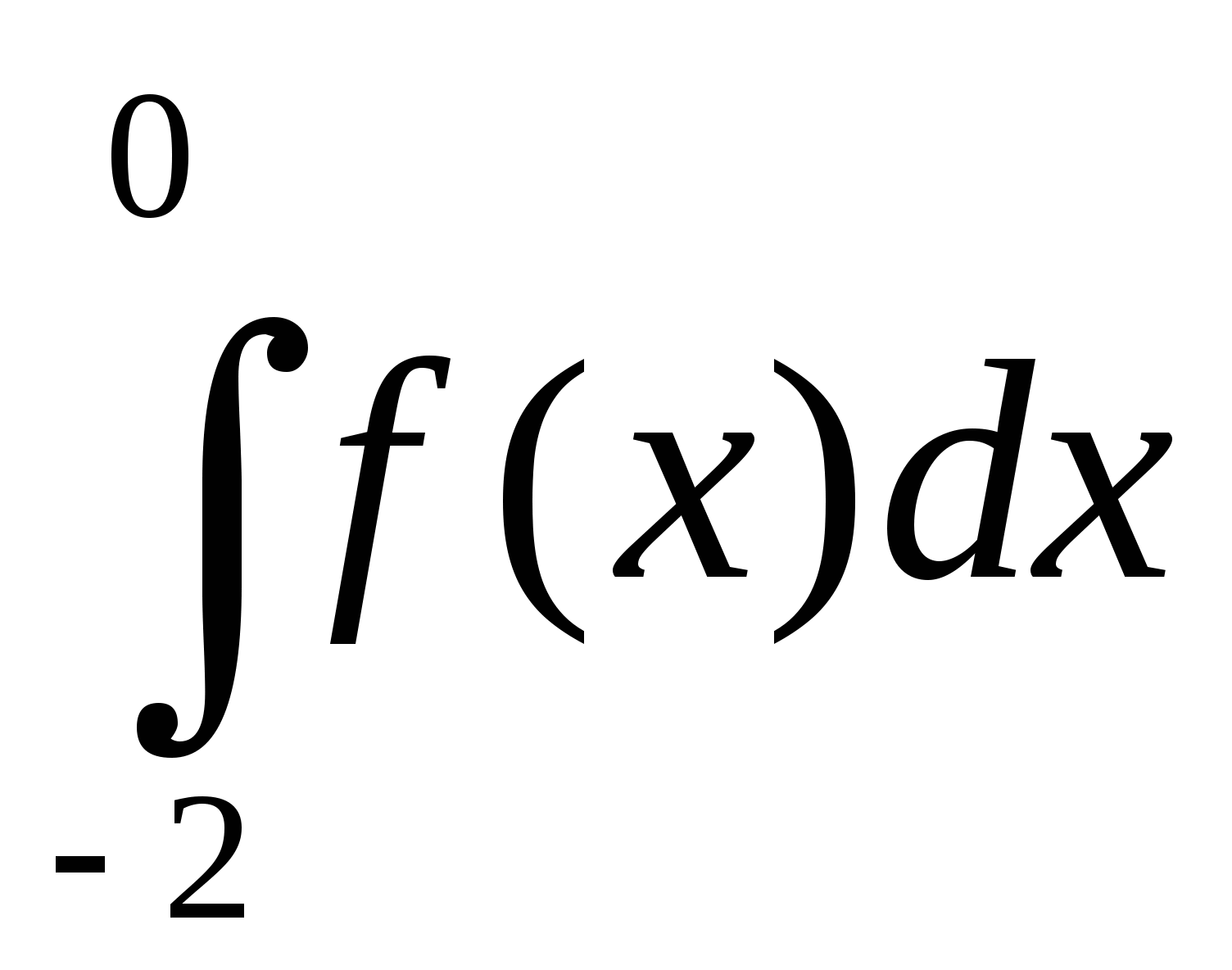
2. Данный интеграл 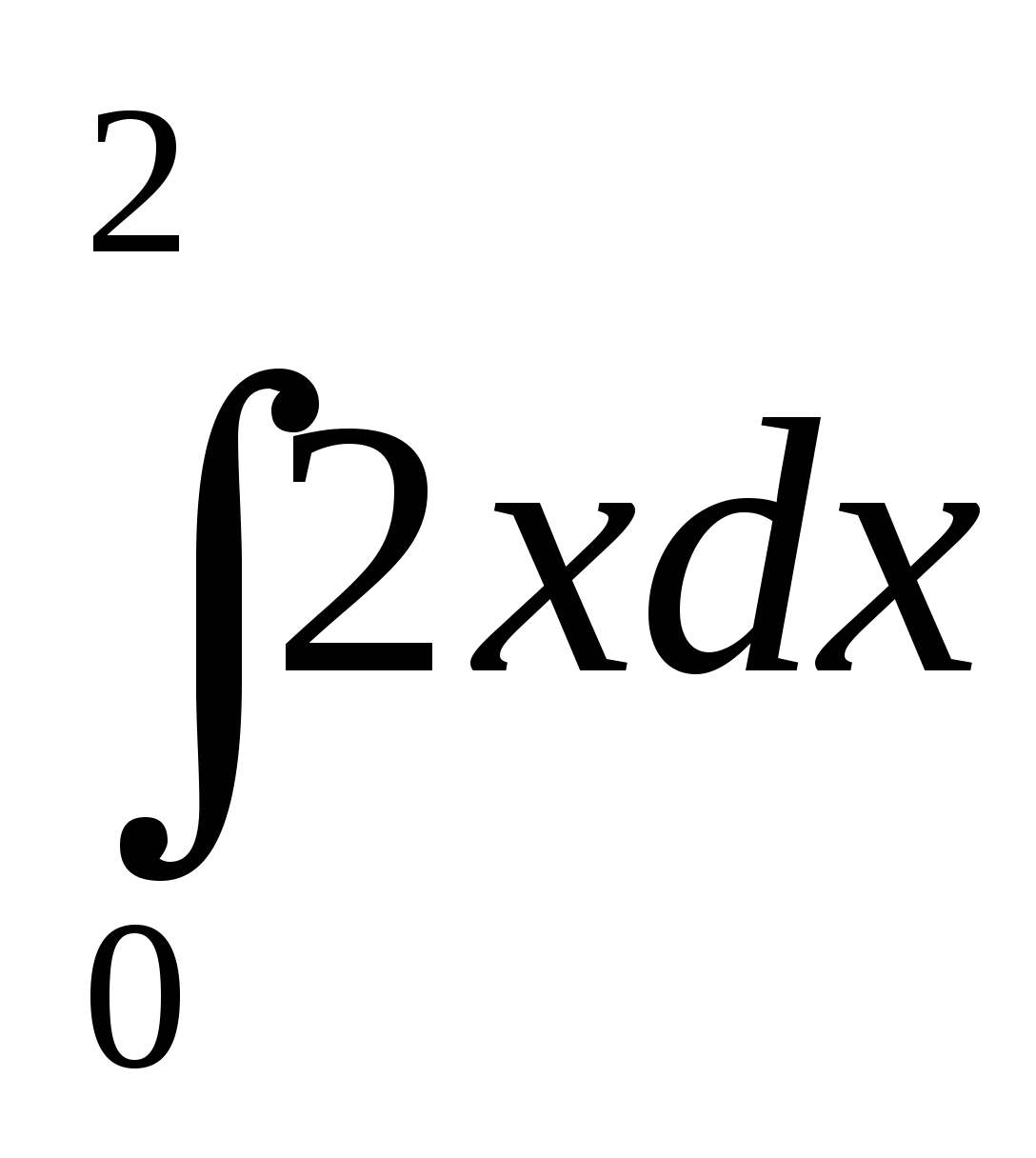равен:

а) 0

б) -4

в) 4

г) 8

3. В данном интеграле 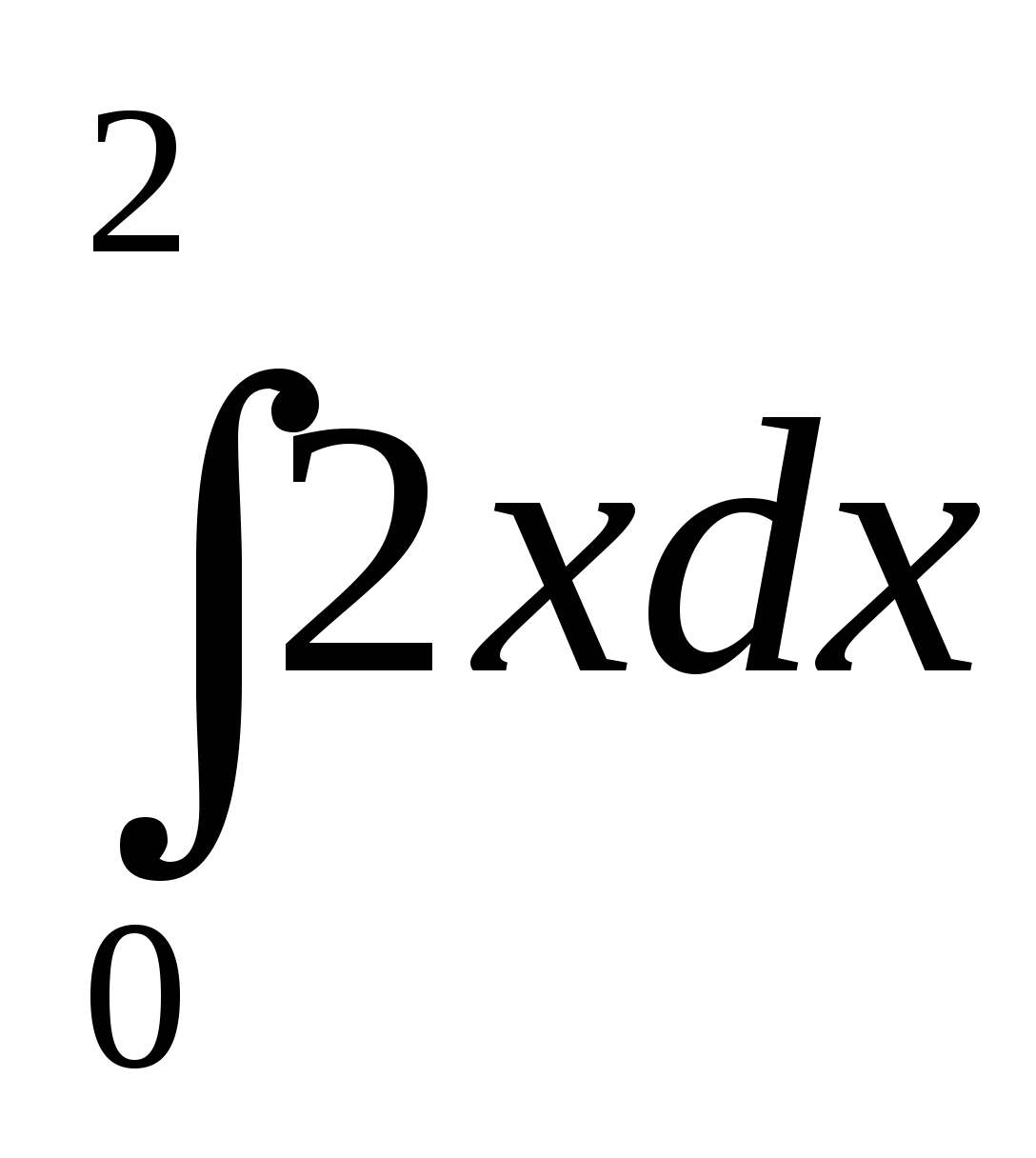подинтегральная функция равна:

а) 2х

б) dх

в) 0

г) 2

4. Данный интеграл 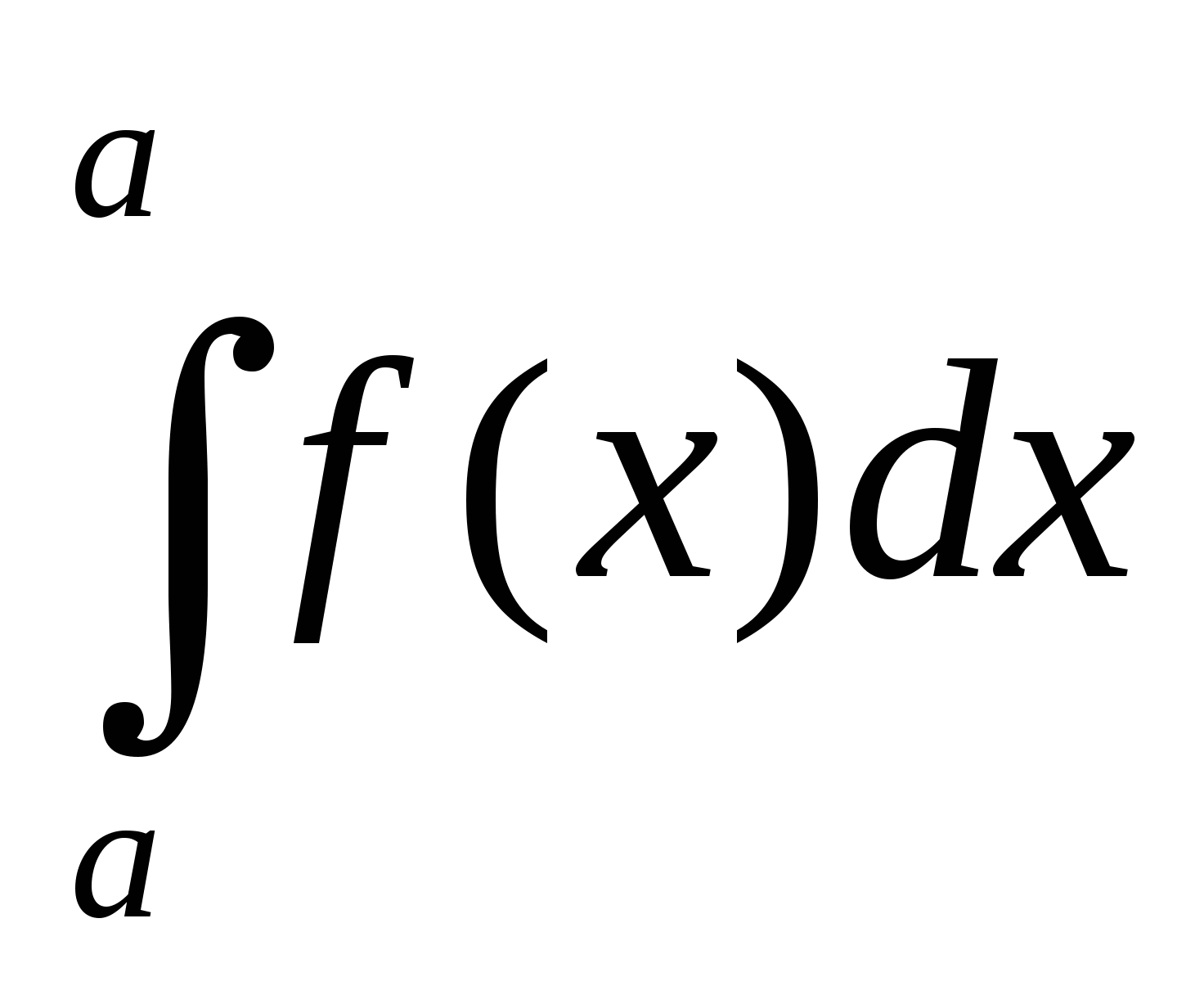равен:

а) 1

б) С

в) 0

г) зависит от подинтегральной функции

5. Выражение данного вида 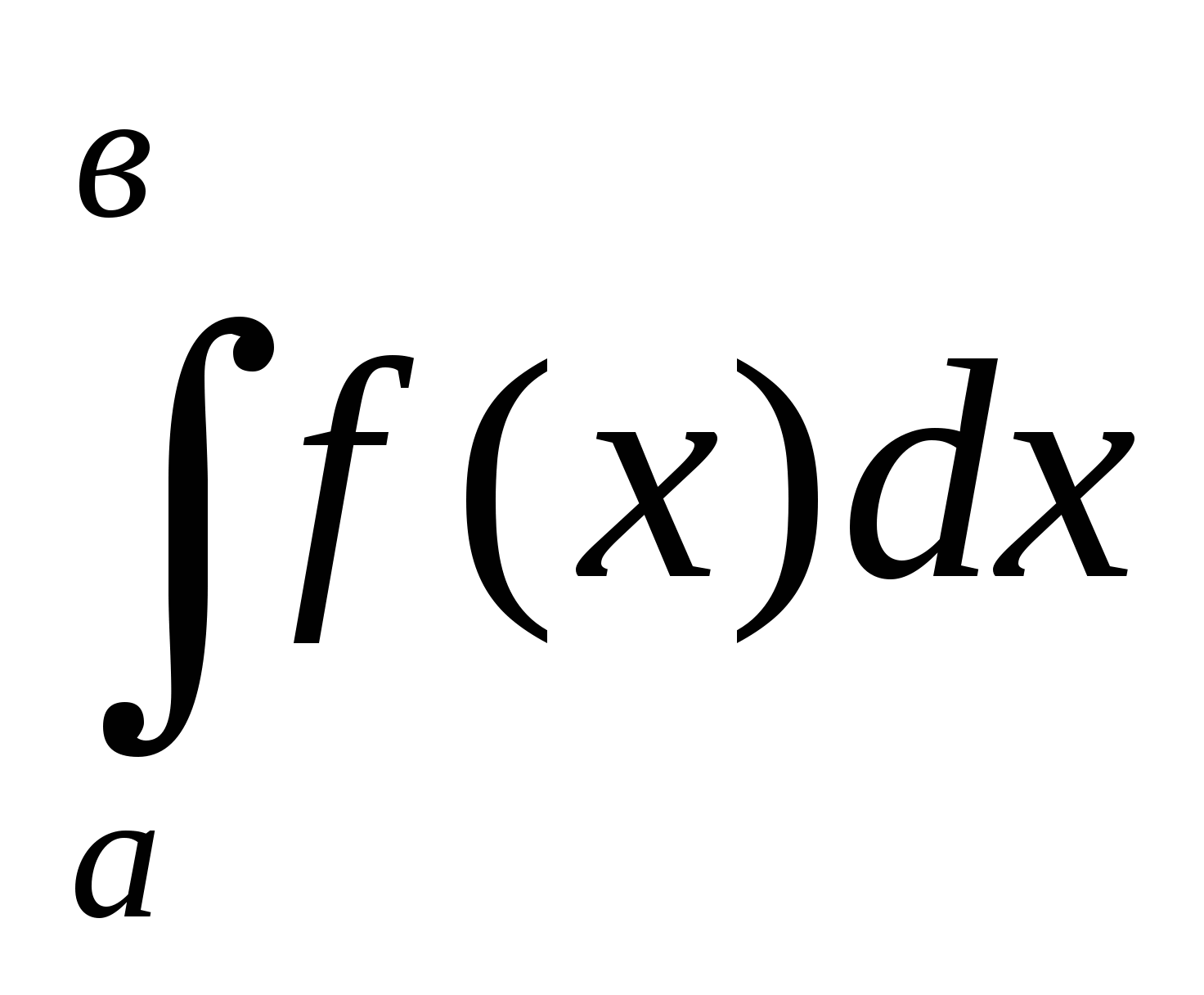называется:

а) определенный интеграл

б) неопределенный интеграл

в) интегралом функции

г) дифференциалом

6. Определенный интеграл вычисляется с помощью формулы:

а) Лейбница

б) Ньютона

в) Лагранжа

г) Ньютона-Лейбница

7. При перестановке пределов интегрирования в определенном интеграле, интеграл ...

а) не изменится

б) увеличится в 2 раза

в) поменяет знак

г) подинтегральная функция изменится на обратную

Приложение 2

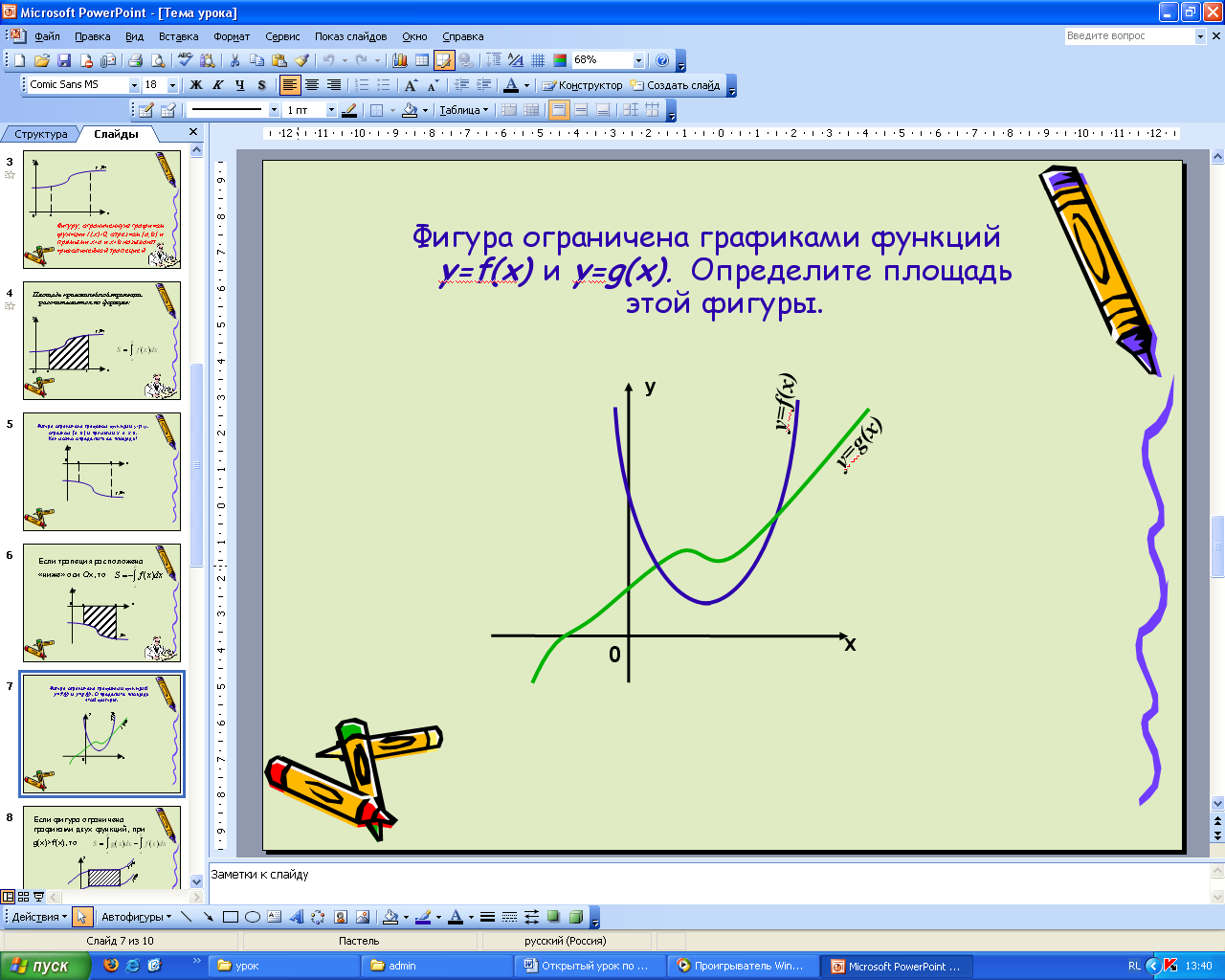
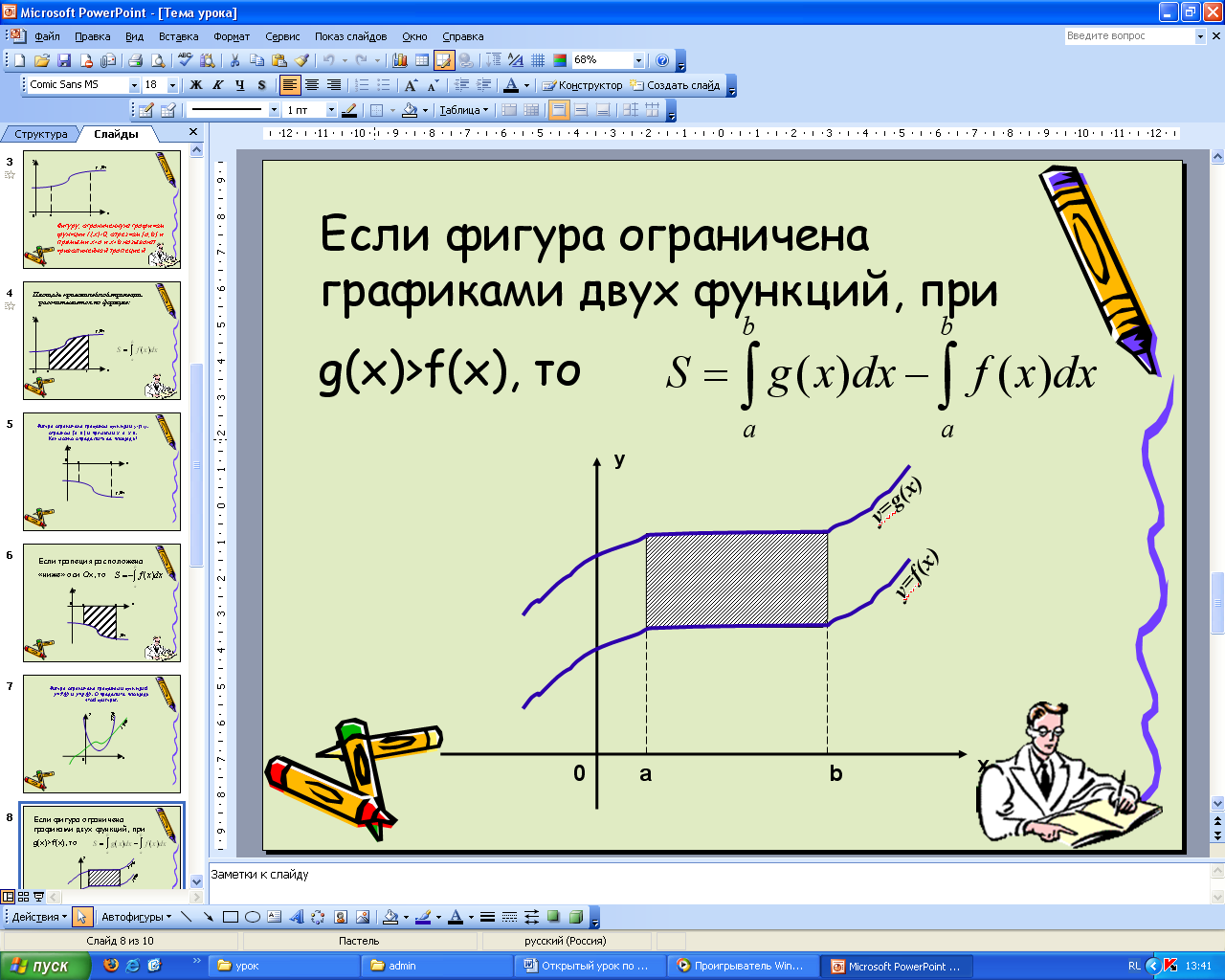
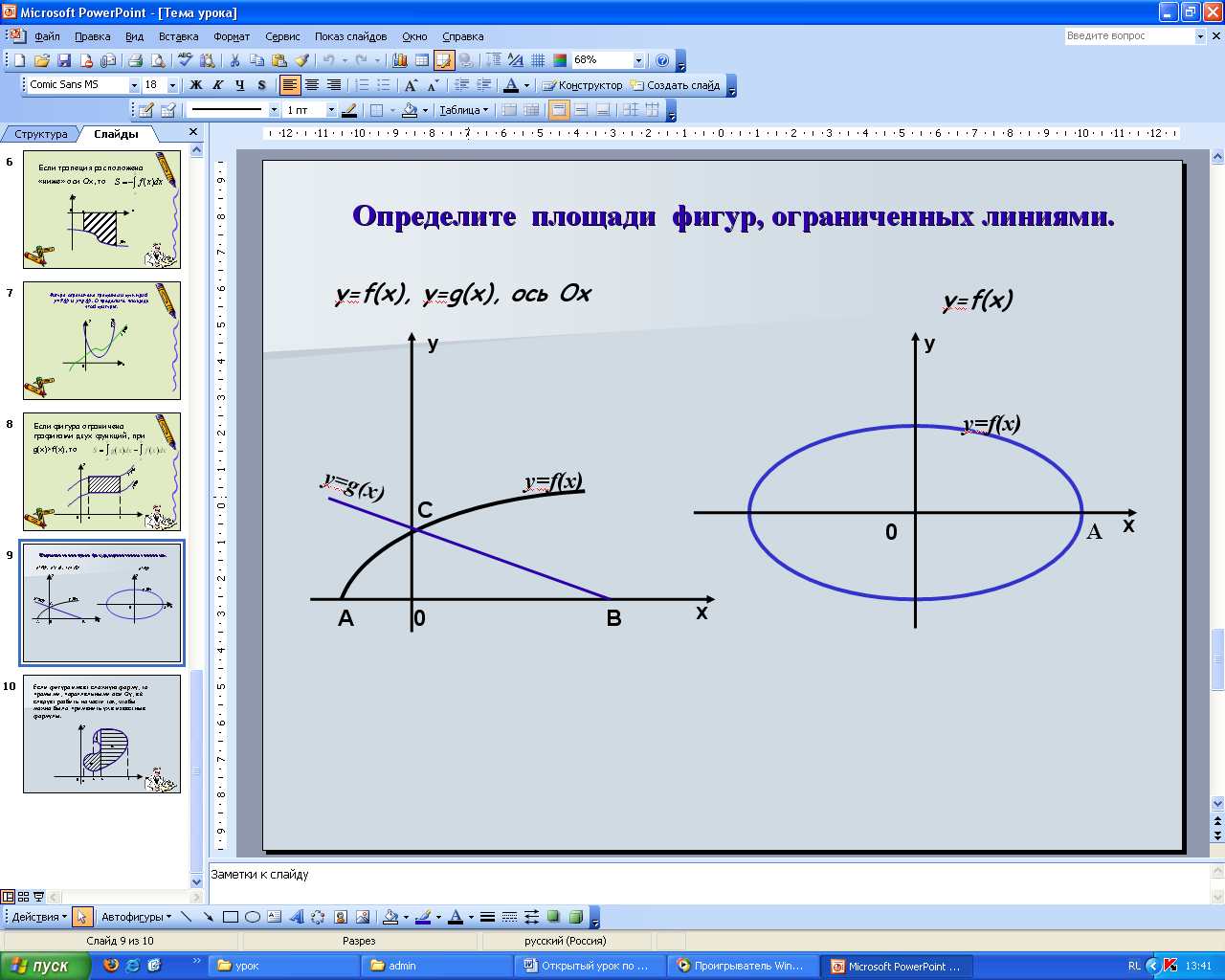
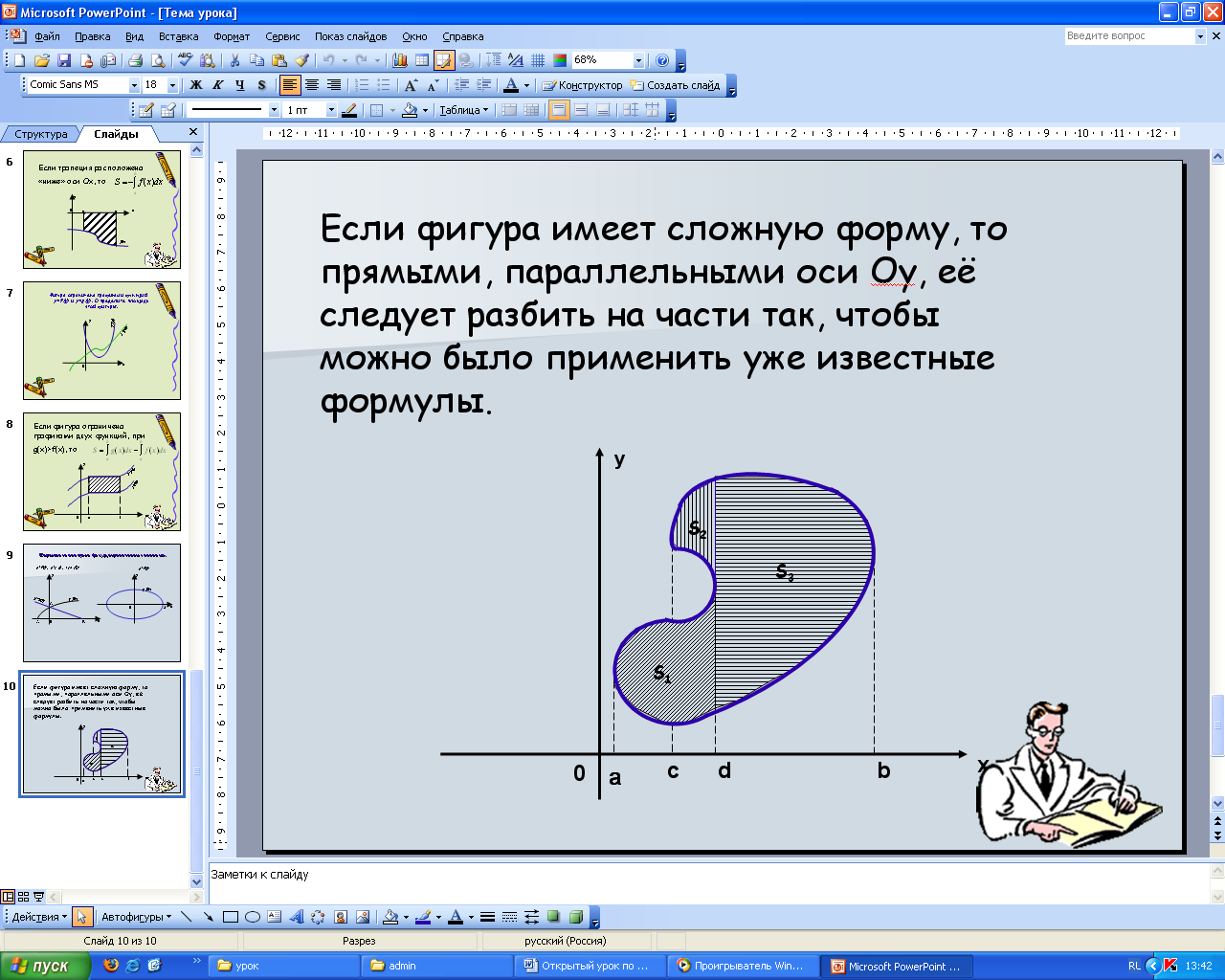
Приложение 3

Приложение 4

Домашняя работа

1. Н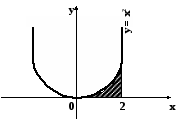айдите площадь криволинейной трапеции, изображенной на рисунке:

2. Н

   yайдите площадь фигуры, изображенной на рисунке:

0

у = sin x

х

0

3. Н

   х

   yайдите площадь фигуры, ограниченной прямой 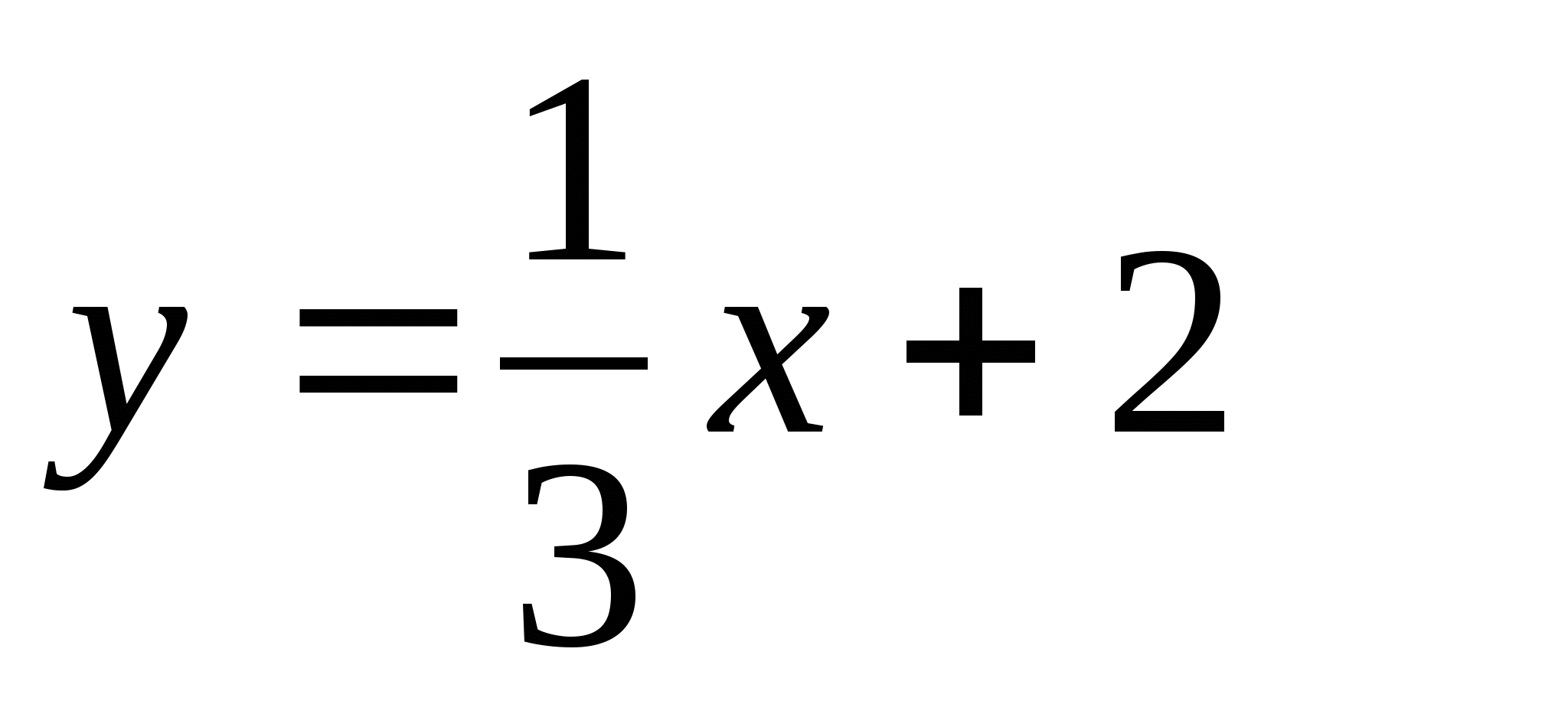и параболой