Конспект урока по теме:Формула Ньютона-Лейбница

Учитель Ступина В.В. 02.02.15г.

Урок по алгебре и началам математического анализа в 11-А классе (физико-математический профиль обучения)

Тема: «Формула Ньютона-Лейбница».

Цели: выучить формулу Ньютона-Лейбница, её практическое применение, сформировать первичные умения и навыки применения этой формулы, развивать абстрактное мышление, математическую речь учащихся, воспитывать культуру умственного труда (коммуникативные, здоровьесберегающие навыки).

Оборудование: проектор, презентация «Исторические сведения», слайды к уроку («Домашнее задание»), раздаточный материал: инструктивные карточки с планом изучения нового материала.

Ход урока:

I.Организационный момент.

II.Повторение ранее изученного:

1.Проверка домашнего задания в парах (меняемся тетрадями)

(слайд на доске)

№6.3(а)

Пользуясь геометрическим смыслом определенного интеграла, вычислите:

; =у; 1-=; +=1 - уравнение окружности с центром в начале координат и радиусом, равным 1.; =

у

х

-1 0 1

Ответ:

№6.33(б)

Пользуясь геометрическим смыслом определенного интеграла, вычислите: dх;

Площадь прямоугольника АКСД равна 3

Площадь треугольника ВКС равна ;

Тогда = 21- 9 =12

K

Cу

7

D

B

A1

0 3 х Ответ:

II. Сообщение темы.

Ш. Целеполагание.

IV. Мотивационный блок урока.

V. Актуализация опорных знаний: для того, чтобы применять формулу Ньютона-Лейбница, нужно знать табличные значения неопределённых интегралов. Интерактивная игра «Задай вопрос» (Две команды задают друг другу вопросы)

(x )

+ C (n)

(x)

(x)

=

VI.Изучение нового материала.

-Краткое сообщение «Исторические сведения о великих ученых И.Ньютоне и Г. Лейбнице», презентация.

- работа в группах по плану (план на экране) с учебником с.185, п.6.6.

План:

1. Теорема Ньютона-Лейбница.

2. Вычисление определённого интеграла по формуле Ньютона-Лейбница.

3.Вычисление площади криволинейной трапеции, ограниченной линиями у=0, х=а, х=в, у=f(х), причем функция у=f(х) на интервале интегрирования принимает положительные и отрицательные значения.

4. Вычисление площади фигуры:

а) ограниченной линиями, у=f(х), х=а, х=в;

б) ограниченной линиями у=у=.

у=f(х), у=у= - функции непрерывные на области интегрирования.

-изложение материала учащимися у доски по плану:

1.Пусть функция f(x)непрерывная на отрезке и пусть F(х) есть какая-либо её первообразная. Тогда справедливо равенство Это равенство называют формулой Ньютона-Лейбница.

4.Вычислим площадь фигуры, ограниченной линиями y= и у= (ученик готовится у доски)

+ (ед.кв.)

y

4

4 C

2

B x

A O 1 2D

Ответ:4,5(ед.кв.)

3. Вычислить площадь криволинейной трапеции, ограниченной графиком функции прямыми (ученик готовится у доски)

у

1 1способ: Ф=

- 0 x

-1 =1-(-1)=2(ед.кв.) -(-1)+1=2(ед.кв.)

(ед.кв.)

Ответ: 4 (ед.кв.)

2 способ:

относительно оординат. Равные фигуры имеют равные площади.

=2-(-1)+1)=4(ед.кв.)

Ответ: 4 (ед.кв.)

2.Объяснение вычисления определённого интеграла по формуле Ньютона-Лейбница

(ученик у доски сразу начинает отвечать)

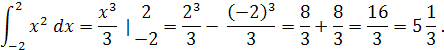
VI. Формирование умений и навыков (продолжим в классе):

1.Учебник с.189 №6.46-№6.48 (формирование умений и навыков применения формулы Ньютона-Лейбница при вычислении определённых интегралов).

2.Практическое применение формулы Ньютона-Лейбница при вычислении площадей фигур, ограниченных линиями: №6.59*(а)

VII. Домашнее задание:п.6.6.-читать, с 185-186 №6.60

VIII. Итог урока.

Тестовые задания

1. Первообразная является функцией обратной:

A) производной;

B) ее области определения;

C) ее области значений;

D) логарифмической функции.

2. Интеграл, с равными пределами интегрирования, равен:

A) единице;

B) нулю;

C) нельзя вычислить;

D) первообразной функции.

3. Формула Ньютона-Лейбница позволяет вычислить:

A) первообразную функции;

B) неопределенный интеграл;

C) площадь криволинейной трапеции;

D) производную функции.

4. Первообразная суммы двух функций равна:

A) сумме первообразных этих функций;

B) разности первообразных этих функций;

C) произведению первообразных этих функций;

D) сумме производных этих функций.

5. Постоянный множитель можно:

A) удалить из произведения;

B) вынести за знак интеграла;

C) заменить на слагаемое;

D) заменить на ноль.

6. Если поменять местами пределы интегрирования, то:

A) результат удвоится;

B) результат не изменится;

C) результат изменит знак;

D) определенный интеграл не вычисляется.

7. Действие, обратное интегрированию, называется:

A) дифференцирование;

B) логарифмирование;

C) потенцирование;

D) извлечение корня.

8. Интеграл - это:

A) множество всех производных для данной функции;

B) множество всех первообразных для данной функции;

C) дифференциал функции;

D) область определения функции.

9. Интеграл - это:

A) среднее значение пределов интегрирования;

B) максимальная точка ординаты криволинейной трапеции;

C) число, показывающее значение площади криволинейной трапеции;

D) число, показывающее значение периметра криволинейной трапеции.

10. Основное свойство первообразной - это:

A) любая первообразная может быть записана в виде F (x) + C;

B) любая первообразная может быть записана в виде F (x) · C;

C) первообразная произведения равна сумме первообразных;

D) первообразную можно определить для любой функции.

Код ответов (1,2,3)