Научно-исследовательская работа Нахождение угла между скрещивающимися прямыми

Содержание.

1.Введение.

2.Теоретическая часть.

3.Практическая часть.

4.Заключение

5.Список используемой литературы

6. Приложение

Введение.

В представленной работе исследуются методы нахождения угла между скрещивающимися прямыми. Решая тесты ЕГЭ, обратил внимание на то, что в них присутствуют задачи такого типа и не всегда их можно решить, используя только один метод. Решая задачи, я всегда ищу более короткое, рациональное, наиболее красивое решение.

Эта работа актуальна потому что, исследуя методы на нахождение угла между скрещивающимися прямыми, у меня появилась возможность расширить полученные на уроках знания, научиться решать задачи новыми способами, а в дальнейшем применять эти знания на олимпиадах и заданиях ЕГЭ. Предметом моих исследований стали геометрические задачи на нахождение угла между скрещивающимися прямыми.

Цели работы:

1. Рассмотреть теоретический аспект угла между скрещивающимися прямыми.

2. Обобщить все знания, полученные в ходе исследования.

3. Сделать выводы.

Задачи:

1. Изучить литературу по данной теме.

2. Познакомиться с новыми методами нахождения угла между скрещивающимися прямыми.

3. Подобрать задачи по данной теме.

4. Исследовать задачи на примере изученных методов и находить наиболее рациональное решение.

Гипотеза: С помощью изученных методов можно найти наиболее рациональное решение олимпиадных задач и заданий ЕГЭ - С2».

Теоретическая часть.

Скрещивающиеся прямые.

Определение: Прямые не лежащие в одной плоскости называются скрещивающимися (см. Рис.1).

Теорема: Если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке не лежащей на первой прямой, то эти прямые скрещивающиеся.

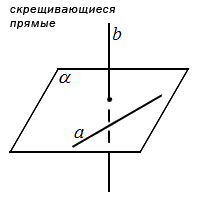
Рисунок 1. Скрещивающиеся прямые.

Угол между скрещивающимися прямыми.

Определение: Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, параллельными данным скрещивающимся прямым (см. рис 2).

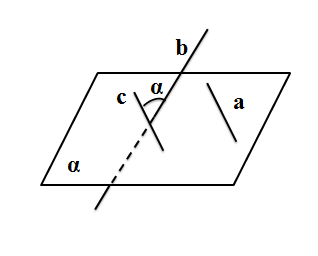
Рисунок 2. Угол между скрещивающимися прямыми b и a.

Способы нахождения угла между скрещивающимися прямыми.

Поэтапно-вчислительный.

Первый способ - с помощью параллельного переноса. Напомним, в чем его суть: мы производим перенос одной из скрещивающихся прямых (или сразу двух) так, чтобы прямые, полученные в результате этого преобразования, пересекались. Тем самым исходная задача сводится к нахождению угла между двумя прямыми на плоскости.

Алгоритм решения:

1. Определение типа прямых.

2. Параллельный перенос одной или обеих прямых.

3. Нахождение требуемого угла.

Пример (см.рис.3).

а) Пусть а и b - данные скрещивающиеся прямые. Через одну из них, например, b и через какую-нибудь точку А, лежащую на прямой а, проведем плоскость α.

б) Через точку А проведем прямую с||b. Получившийся ∠MAN- угол между скрещивающимися прямыми.

в) Выберем на прямой а - какую-нибудь точку М, а на прямой с - точку N. Получим треугольник AMN. Вычислим стороны треугольника по теореме косинусов и найдем .

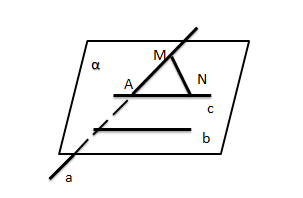
Рисунок 3. Поэтапно-вычислительный метод.

Метод трех косинусов.

Алгоритм:

1. Определить тип прямых.

2. Спроектировать скрещивающуюся прямую на плоскость.

3. Найти косинус

4. Нахождение искомого угла.

Пример (см. рис. 4).

а) а и b-скрещивающиеся прямые. Проведем через прямую а плоскость α пересекающую прямую b.

б) Спроектируем b на α. b1- проекция.

в)

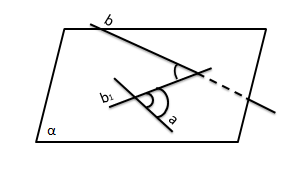
Рисунок 4. Метод трех косинусов.

Метод проектирования обеих скрещивающихся прямых на плоскость перпендикулярную одной из них.

Пример (см. рисунок 5).

а) а и b - скрещивающиеся прямые.

б) Плоскость α перпендикулярна прямой а, b пересекает α в точке В, точка А - проекция прямой а, а прямая b1 проекция прямой b.

в) На прямой b лежит отрезок длинной d, а его проекция на плоскость α имеет длину d1.

г) Тогда верна формула , где α- угол между прямыми а и b.

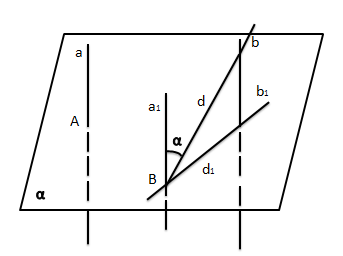
Рисунок 5. Метод проектирования обеих скрещивающихся прямых на плоскость перпендикулярную одной из них.

Метод проектирования отрезка одной из скрещивающихся прямых на другую (см. прил. 9).

Пример (см.рис. 6):

а) a и b - скрещивающиеся прямые.

б) На прямой a находится отрезок длины d, и его ортогональной проекцией на прямую b является отрезок длиной d1.

в) Тогда верна формула , где α - угол между прямыми a и b.

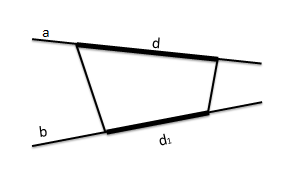
Рисунок 6. Метод проектирования отрезка одной из скрещивающихся прямых на другую.

Метод тетраэдра.

Весьма эффективный метод, но встречается достаточно редко.

Пример (см. рис. 7).

Для тетраэдра верна формула .

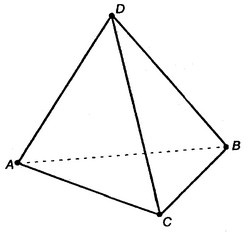
Рисунок 7. Метод тетраэдра.

Я подробней остановлюсь на самом универсальном на мой взгляд, самом доступном для понимания, координатном методе.

Координатный метод.

Алгоритм:

1. На рисунке изображаем указанные в задаче прямые (которым придаем направление, т.е. векторы).

2. Вписываем фигуру в систему координат.

3. Находим координаты концов векторов.

4. Находим координаты Векторов.

5. Подставляем в формулу "косинус угла между векторами".

6. После чего (если требуется в задаче), зная косинус, находим значение самого угла.

Чтобы освоить этот метод, надо хорошо уметь находить координаты точки в пространстве и правильно располагать многогранники в системе координат. Более подробно с расположением стереометрических фигур в системе координат вы можете ознакомиться в приложение (см. прил. 1-6).

Формула косинуса угла между векторами.

,

где .

Практическая часть.

Задача №1. На ребре ВВ1 куба ABCDA1B1C1D1 взята точка К так, что BK:KB1=3:1. Найдите угол между прямыми AK и BD1 (см. рис.8).

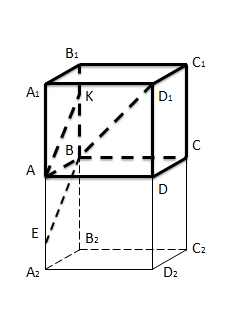
Рисунок 8. Задача №1.

1) AK и BD1 - скрещивающиеся прямые.

2) Д.П. достроим куб до призмы A1B1C1D1A2B2C2D2, где ABCDA2B2C2D2-куб. Отметить точку Е на АА1 так, что АЕ : ЕА2=3:1. Тогда AK параллельна BE. Рассмотрим треугольник EBD1. Возьмем сторону АВ=1; BE =1.25 (по теореме Пифагора).

3), по правилу параллелепипеда.

4), по теореме Пифагора.

по теореме косинусов.

5)Получим , где α искомый угол.

Ответ: .

Пример решения этой же задачи можете пронаблюдать в приложение (см.прил.7-8).

Задача №2. В правильный 4-х угольной призме ABCDA1B1C1D1 сторона основания равна 2,боковое ребро равно 1. Найдите угол между АА1 и B1D(см.рис.9).

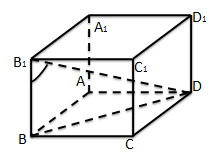
Рисунок 9. Задача №2.

1. АА1 и B1D - скрещивающиеся прямые.

2. т. А - проекция АА1, на плоскость ABC.

3. BD- проекция BD1-на АВС, тогда

4. ;

Ответ:.

Задача №3. В правильной 6-ти угольной пирамиде АВС…F1 сторона основания равна корню квадратному из 2-х, а боковое ребро равно 1. Найдите угол между АF1 и B1C(см. рис. 10).

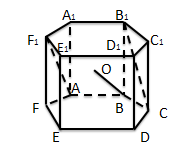
Рисунок 10. Задача №3

1. AF1 и B1C- скрещивающиеся прямые.

2. F1A||BO, где O-центр 6-ти угольника ABCDEF.

3. Рассмотрим тетраэдр OBB1C:, по теореме Пифагора; в правильном треугольнике OB1A1;BB1=1;BC= по условию

Ответ:.

Задача №4. В правильной треугольной призме все ребра равны 1. Найдите угол между прямыми AС1 и СB1.

10