Урок по геометрии по теме 'Вписанная окружность'

Урок по теме «Параллельные прямые»

Цель урока: формирование знаний о параллельных прямых.

Задачи урока:

Образовательные:

· ввести понятие параллельных прямых;

· научить школьников распознавать параллельные прямые на чертеже;

· научить строить параллельные прямые;

· познакомить с историей развития теории о параллельных прямых;

· показать актуальность темы.

Развивающие:

· развивать логическое мышление, память, математическую речь;

· развивать организационные умения;

· развитие творческой самостоятельности и инициативы.

Воспитательные:

· · формирование деятельностных познавательных интересов обучающихся;

· стимулировать мотивацию и интерес к изучению предмета.

Ход урока

I. Анализ самостоятельной работы.

II. Актуализация знаний

1. Какие прямые называются перпендикулярными?

2. С помощью каких инструментов можно построить перпендикулярные прямые?

III. Объяснение материала

ответ

ответ

число

буква

число

буква

1) -17+33=

1) -17+33=

2) -3 *(-5)=

2) -3 *(-5)=

3)-156:(-12)=

3)-156:(-12)=

4) 12,3+2,7=

4) 12,3+2,7=

5) -2-3+11=

5) -2-3+11=

6) -18: ( - 3)=

6) -18: ( - 3)=

7) 0,1+0,2+10-0,3-1=

7) 0,1+0,2+10-0,3-1=

8) 138:23=

8) 138:23=

9) 6,84:0,36=

9) 6,84:0,36=

10) 6,25:1,25=

10) 6,25:1,25=

л

п

о

р

а

е

с

6

16

19

13

15

9

5

Название параллельных прямых произошло от греческого слова «параллелос», что значит «идущие рядом». Для обозначения параллельных прямых древнегреческие математики использовали знак «=», однако 18 веке этот знак начали использовать для обозначения равенства чисел или выражений. А параллельные прямые начали обозначать «‖».

Приведите примеры параллельных прямых в окружающей обстановке.

1. Две различные прямые могут либо пересекаться в одной точке либо не пересекаться. (Показать на спицах или на других предметах окружающей обстановки.)

Если рельсы железнодорожного пути изобразить прямыми линиями, то эти линии будут идти рядом, нигде не пересекаясь, - они параллельны.

2. Определение параллельных прямых: прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. Название произошло от греческого «параллелос», что означает «идущий рядом».

3. Обозначение параллельности: MN || АВ (рис. 104 учебника).

Если АВ || MN, то MN || АВ.

4. Как и в случае перпендикулярности линий, можно говорить о параллельных отрезках, лучах.

5. Определение параллельных отрезков (лучей) (рис. 105, 106 учебника).

6. Рассмотреть рисунок 107 учебника и записать в тетрадях вывод: Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны: а  в и с  в, то а || с.

Поэтому противоположные стороны любого прямоугольника параллельны (рис. 108).

Они образуют прямые углы с двумя другими сторонами этого прямоугольника.

Параллельные линии можно обнаружить в разлиновке ваших тетрадей, на шахматной доске и много где еще.

7. Именно это свойство используют как при построении параллельных прямых, так и для проверки их параллельности (рис. 109).

8. На доске показать построение параллельных прямых с помощью линейки и чертежного треугольника. Учащиеся выполняют построение в тетрадях.

9. На плоскости проведена прямая и отмечена точка, не лежащая на этой прямой. Сколько прямых, параллельных данной, можно провести через эту точку? Сделать вывод.

Постройте в тетрадях прямоугольник ABCD. Назовите его противоположные стороны. Продолжите стороны ВС и AD за пределы прямоугольника. Что вы можете сказать про эти прямые? Как вы думаете, пересекутся ли эти прямые, если их продолжить еще дальше? (Нет)

IV. Закрепление изученного материала.

1. Решить № 1370 на доске и в тетрадях.

2. Решить № 1373 устно по рис. 110 учебника.

3. Решить № 1374 на доске и в тетрадях.

4. Начертите какой-нибудь четырехугольник. Соедините отрезками середины смежных сторон. Проверьте, будут ли параллельны противоположные стороны нового четырехугольника.

Ответ: Да, параллельны.

5. Постройте четырехугольник АВСД, в котором АВ || СД.

6. Постройте пятиугольник, у которого две стороны параллельны.

7. Решить № 1375 на доске и в тетрадях.

8. Решить № 1383 (1) самостоятельно с проверкой.

V. Итог урока.

Ответить на вопросы п. 44 на с. 241 учебника.

Домашнее задание: выучить правила п. 44, решить № 1384 (рис. 112, а; б), № 1386, № 1388, № 1389 (а).

ответ

ответ

число

буква

число

буква

1) -17+33=

1) -17+33=

2) -3 *(-5)=

2) -3 *(-5)=

3)-156:(-12)=

3)-156:(-12)=

4) 12,3+2,7=

4) 12,3+2,7=

5) -2-3+11=

5) -2-3+11=

6) -18: ( - 3)=

6) -18: ( - 3)=

7) 0,1+0,2+10-0,3-1=

7) 0,1+0,2+10-0,3-1=

8) 138:23=

8) 138:23=

9) 6,84:0,36=

9) 6,84:0,36=

10) 6,25:1,25=

10) 6,25:1,25=

ответ

ответ

число

буква

число

буква

1) -17+33=

1) -17+33=

2) -3 *(-5)=

2) -3 *(-5)=

3)-156:(-12)=

3)-156:(-12)=

4) 12,3+2,7=

4) 12,3+2,7=

5) -2-3+11=

5) -2-3+11=

6) -18: ( - 3)=

6) -18: ( - 3)=

7) 0,1+0,2+10-0,3-1=

7) 0,1+0,2+10-0,3-1=

8) 138:23=

8) 138:23=

9) 6,84:0,36=

9) 6,84:0,36=

10) 6,25:1,25=

10) 6,25:1,25=

ответ

ответ

число

буква

число

буква

1) -17+33=

1) -17+33=

2) -3 *(-5)=

2) -3 *(-5)=

3)-156:(-12)=

3)-156:(-12)=

4) 12,3+2,7=

4) 12,3+2,7=

5) -2-3+11=

5) -2-3+11=

6) -18: ( - 3)=

6) -18: ( - 3)=

7) 0,1+0,2+10-0,3-1=

7) 0,1+0,2+10-0,3-1=

8) 138:23=

8) 138:23=

9) 6,84:0,36=

9) 6,84:0,36=

10) 6,25:1,25=

10) 6,25:1,25=

л

п

о

р

а

е

с

6

16

19

13

15

9

5

л

п

о

р

а

е

с

6

16

19

13

15

9

5

л

п

о

р

а

е

с

6

16

19

13

15

9

5

л

п

о

р

а

е

с

6

16

19

13

15

9

5

л

п

о

р

а

е

с

6

16

19

13

15

9

5

л

п

о

р

а

е

с

6

16

19

13

15

9

5

л

п

о

р

а

е

с

6

16

19

13

15

9

5

л

п

о

р

а

е

с

6

16

19

13

15

9

5

Тема: Описанная окружность.

Цель: Формирование навыков самостоятельной познавательной деятельности в процессе проблемного диалога

Задачи:

• уметь выделять существенные признаки вписанной и описанной окружности и на основе их давать определения;

• уметь, пользуясь определением, классифицировать окружности;

• переводить язык чертежа на математический я зык и язык разговорный;

• строить умозаключения о свойствах фигур по примерам на основе ранее доказанных теорем и их следствий.

Ход урока.

1. Организация начала урока

2. Актуализация знаний

Тест

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.

2. Центром вписанной в треугольник окружности является точка пересечения:

• Биссектрис треугольника

• Высот треугольника

• Медиан треугольника

• Серединных перпендикуляров к сторонам треугольника.

3. Вписанная в четырехугольник окружность изображена на рисунке:

б

а

в

4. В треугольник можно вписать только _________________________.

5.Вписанная в треугольник окружность изображена на рисунке:

а

б

в

г

3. Изучение нового материала

-Рассмотрите рисунки и выделите группы рисунков.(вписанные)

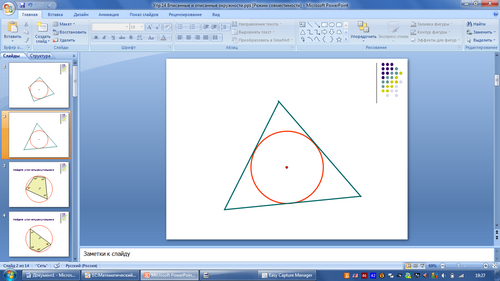
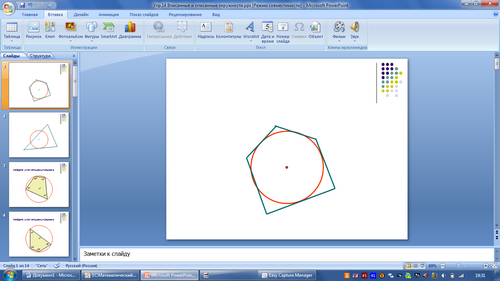
Рисунок 1

Рисунок 2

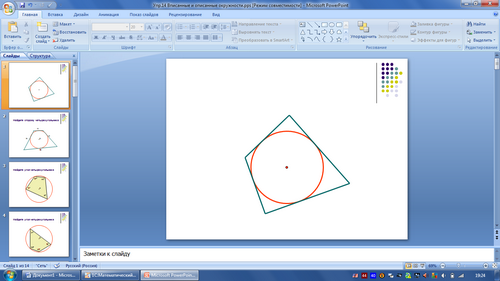
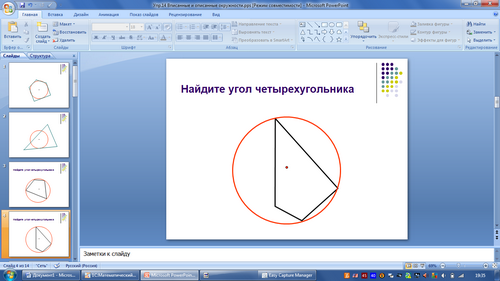
Рисунок 3

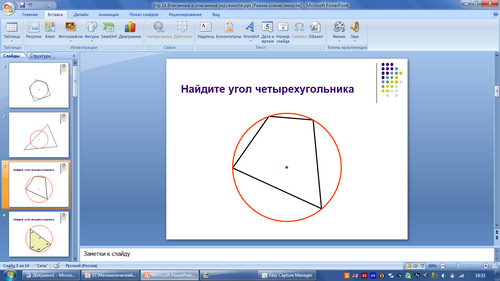
Рисунок 4

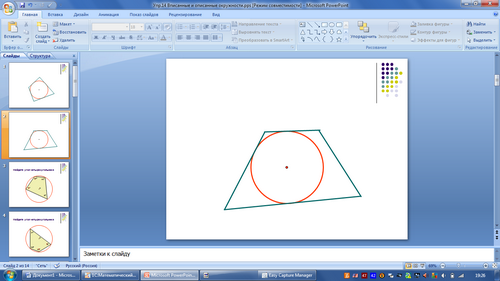
Рисунок 5

Рисунок 6

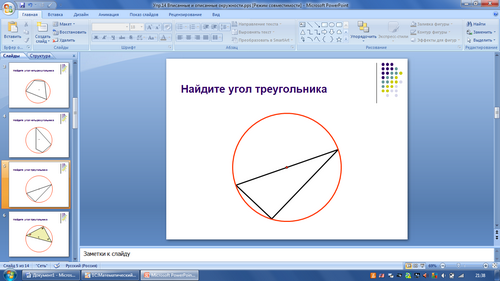
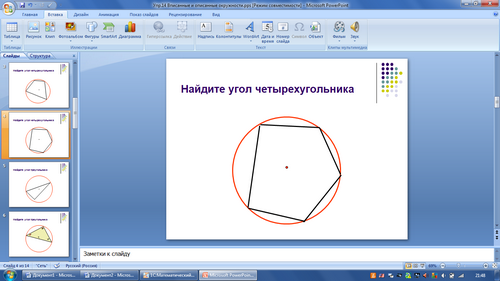
Рисунок 7

Рисунок 8

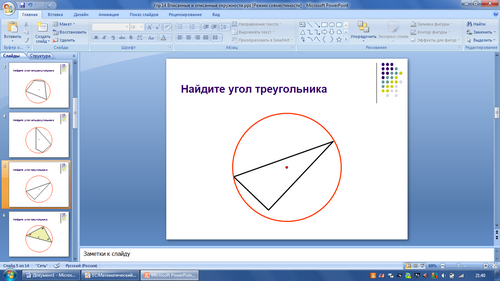
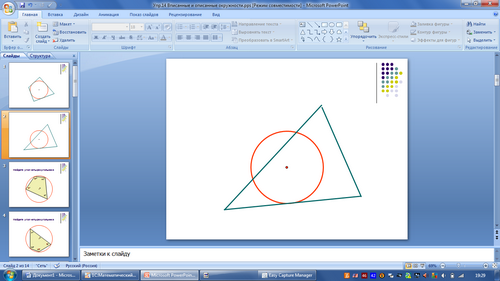
Рисунок 9

Рисунок 10

- Определите по оставшимся рисункам тему урока.

- Какие вопросы нам нужно разрешить?

Описанная окружность

1. Определение

2. Связь с треугольником

3. связь с четырёхугольником

Из оставшихся рисунков выделите те, на которых на ваш взгляд описанная окружность.

- Найдите определение описанной окружности в учебнике. Подходят наши окружности под определение?

- Перейдём ко второму вопросу.

- Что необходимо определить у окружности?

- Где может находиться точка, равноудалённая от вершин?

- Всегда ли есть такая точка у треугольника? Сколько их?

- Итак, сделаем вывод об описанной окружности около треугольника, её центре и радиусе.

-С опорой на что поведём речь при рассмотрении третьего вопроса? Посмотрите внимательно на рисунок и определите какая связь между углами четырёхугольника.

-Какой вывод можно сделать?

4. Первичное закрепление материала

1.решить № 702

2. Решить № 703

3. решить 706

5. Итог урока

решение нестандартных задач

1. Некто имеет сад в форме правильного треугольника, в вершинах которого дерево здоровья, хорошего настроения и удачи. Может ли он сделать беговую дорожку по кругу так, чтобы каждый раз задевать эти три дерева рукой? Если да, то как?

6. Домашние задание .

вопросы 24, 25, с. 188; №№ 711 (для прямоугольного и равностороннего треугольников), 705

Тест

5. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.

6. Центром вписанной в треугольник окружности является точка пересечения:

• Биссектрис треугольника

• Высот треугольника

• Медиан треугольника

• Серединных перпендикуляров к сторонам треугольника.

7. Вписанная в четырехугольник окружность изображена на рисунке:

б

а

в

8. В треугольник можно вписать только _________________________.

5.Вписанная в треугольник окружность изображена на рисунке:

а

б

в

г

Тест

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.

2. Центром вписанной в треугольник окружности является точка пересечения:

• Биссектрис треугольника

• Высот треугольника

• Медиан треугольника

• Серединных перпендикуляров к сторонам треугольника.

3. Вписанная в четырехугольник окружность изображена на рисунке:

б

а

в

4. В треугольник можно вписать только _________________________.

5.Вписанная в треугольник окружность изображена на рисунке:

а

б

в

г

Рисунок 1

Рисунок 2

Рисунок 3

Рисунок 4

Рисунок 5

Рисунок 6

Рисунок 7

Рисунок 8

Рисунок 9

Рисунок 10