Конспект урока по геометрии 8 класс по теме 'Площадь параллелограмма'

Разработка урока геометрии по технологической карте.

Тема: Площадь параллелограмма (8 класс).

Предмет, класс

Геометрия - 8 класс

ФИО учителя

Игнатьева Лариса Викторовна

Тема

Площадь параллелограмма.

Цель темы

Вывести формулу площади параллелограмма.

Основное содержание темы, термины и понятия

Вывод формулы площади параллелограмма. Площадь параллелограмма.

Тип урока:

Открытие новых знаний

Цели урока:

• образовательные цели направлены на выведение формулы площади параллелограмма;

• развивающие цели данного урока направлены на развитие у учащихся аналитико-синтезирующего, абстрактного мышления, развитие умений применять знания в различных ситуациях;

• воспитательные цели данного урока направлены на формирование у учащихся положительной мотивации, созданию «ситуации успеха» на уроке.

Методы и приемы обучения:

методы проблемного обучения: эвристический метод (постановка проблемы и организация совместной поисковой деятельности по ее разрешению);

методы организации учебно-познавательной деятельности: практические (закрепление умений и навыков происходит в ходе выполнения практических заданий), словесные.

Формы обучения:

фронтальная (на этапе изучения нового материала ведется работа со всем классом, что необходимо для закрепления материала обязательного уровня всеми учениками класса),

индивидуальная и групповая (учащиеся работают самостоятельно и в группах).

Задачи урока:

1.Повторить свойства площадей фигур; формулы площади прямоугольника и квадрата; вывести формулу для нахождения площади параллелограмма; рассмотреть задачи с ее применением.

2. Развивать умения анализировать, сопоставлять, логически мыслить, обобщать; развивать внимание, память, активность и самостоятельность.

3. Воспитывать умение работать в коллективе; воспитывать в учащихся личностную рефлексию: стал ли он сам для себя изменяющимся субъектом деятельности.

Оборудование:

компьютер, мультимедийный проектор, карточки с текстом вывода формулы площади параллелограмма. Урок проводится с использованием мультимедийной презентации Power Point.

Планируемый результат

Предметные умения

УДД

Уметь выводить формулу для вычисления площади параллелограмма.

Уметь устанавливать логические отношения между данными и искомыми.

Использовать для решения геометрических задач графические модели в соответствии с содержанием задания.

Личностные: осознание математической составляющей окружающего мира.

Регулятивные: осознание возникшей проблемы, определение последовательности и составление плана и последовательности действий для решения возникшей проблемы, внесение необходимых дополнений и коррективов в план и способ действия в случае расхождения эталона, реального действия и его результата с учётом оценки этого результата самим обучающимся, учителем, товарищами;

Познавательные: моделирование ситуации из жизни, постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера, выбор наиболее эффективных способов решения задач в зависимости от конкретных условий, рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; владение монологической и диалогической формами речи, умение работать индивидуально и в парах.

Организация пространства.

Межпредметные связи

Формы работы

Ресурсы

Черчение, алгебра, технология, повседневная жизнь

Фронтальная, в группах, индивидуальная

Ученик "Геометрия 7-9" п/р Атанасяна

Методическое пособие

ЭОР - презентация "Задачи на готовых чертежах"

Наглядный и раздаточный материал

Этап

Деятельность учителя

Деятельность учащихся

УУД

Цель этапа

1) включить учащихся в учебную деятельность:

2) определить содержательные рамки урок: продолжаем работать над формулами для вычисления площадей фигур.

1. Самоопределение к деятельности. Организационный момент

Сегодня на уроке мы продолжим разговор о нахождении площадей многоугольников. Мы повторим известные нам свойства площадей, изученные формулы площадей некоторых видов многоугольников, применение их при решении задач, продолжим исследование одного из видов многоугольников с целью вычисления его площади.

Нам на уроке пригодятся:

- хорошее настроение,

- знание материала,

- желание открыть истину,

- добросовестная работа,

- осмысление произведенной деятельности.

Подготовка класса к работе.

Личностные: самоопределение;

регулятивные: целеполагание;

коммуникативные:

планирование сотрудничества с учителем и сверстниками.

Цель этапа:

1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала:

2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;

3) зафиксировать все понятия и алгоритмы в виде символов;

4) зафиксировать индивидуальное затруднение в деятельности, самостоятельно найти выход из ситуации.

2. Актуализация знаний и фиксация затруднения в деятельности.

Посмотрите на картинку слайда. Какие свойства геометрических фигур иллюстрируют следующие рисунки? (Слайд 3, 4, 5,6).

На какие определения, теоремы и свойства мы опирались при доказательстве теоремы о площади прямоугольника?

Проверка домашнего задания

В ходе изучения четырехугольников вы выполняли практические задания по «перекраиванию» различных фигур. Давайте посмотрим некоторые из возможных «перекраиваний» одних многоугольников в другие, которые вы выполнили к уроку.

Используя анимационные возможности презентации продемонстрировать возможные "перекраивания" фигур. (Слайд 7,8,9)

Что сохранилось у прямоугольника и треугольника?

Как называются такие фигуры?

Посмотрите второй способ «перекраивания» равнобедренной трапеции в параллелограмм.

За исключением второй задачи, какой вывод можно сделать?

2. Заранее подготовлены ЭОР "Задачи на готовых чертежах":

1) Стороны прямоугольника 2 см и 4,5 см. Чему равна сторона равновеликого квадрата?

2)

К

А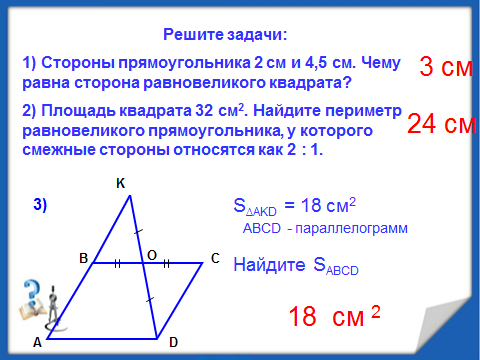

Площадь треугольника АКД равна 18 см² АВСД - параллелограмм. Найдите площадь параллелограмма.

1. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

2. Равные фигуры имеют равные площади.

3. Площадь квадрата равна квадрату его стороны.

4. Площадь прямоугольника равна произведению смежных сторон.

При доказательстве теоремы мы опирались на формулы площади квадрата, на формулы сокращенного умножения (квадрат суммы), на свойства площадей многоугольников.

Показывают выполненные дома, «перекроенные» фигуры:

1. прямоугольник в равнобедренный треугольник;

Площадь

Площадь

Фигуры, имеющие равные площади, называются равновеликими.

2) прямоугольник в равнобедренный треугольник, так чтобы площадь треугольника была равна половине площади прямоугольника;

3) равнобедренную трапецию в параллелограмм;

4)параллелограмма в прямоугольник.

При каждом «перекраивании» одной геометрической фигуры в другие- фигуры оставались равновеликими, т.е. имеющими равные площади.

Устанавливают логические отношения между данными и искомыми величинами.

Выбирают способ решения задачи.

Выдвигаются версии при ответе на вопрос, т.к. неизвестно по какой формуле находится площадь.

Фиксируется затруднение в деятельности.

Предметные: установление логических связей между данными и искомыми величинами, использование для решения геометрических задач графических моделей.

Познавательные: анализ задачи с целью выявления существенных признаков, выбор эффективного способа решения, контроль и оценка результатов деятельности.

Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли, опираясь на определения и теоремы.

Цель этапа:

организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;

3. Постановка учебной задачи.

Создает проблемную ситуацию: В домашней работе, с какой фигурой работали наиболее часто при «перекраивании» и вторая задача в устном счете бала на нахождении чего?

Попробуйте спрогнозировать тему урока.

Попробуем сформулировать наши дальнейшие действия (цель)

При работе дома наиболее часто при «перекраивании» встречался параллелограмм. Вторая задача в устном счете бала на нахождении чего?

Площадь параллелограмма.

Вывести формулу вычисления площади параллелограмма.

Перед учащимися возникает проблема: как найти площадь параллелограмма?

Регулятивные: целеполагание.

Познавательные: самостоятельное выделение и

формулирование проблемы.

Цель этапа:

1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;

2) зафиксировать новый способ действия

4. Построение проекта выхода из затруднения.

Возьмите в руки макет параллелограмма и попробуйте «перекроить» его в равновеликую фигуру, площадь которой мы умеем вычислять.

В

А

К

Н

D

С

Проведем в параллелограмме ABCD высоты ВН и СК. Что можно сказать об отрезках АВ и СD ?

Что вы можете сказать о треугольниках АВН и DCK? Почему?

А что мы знаем о площадях равных фигур?

Посмотрите на чертеж параллелограмма. Из каких двух фигур он состоит?

Переместим треугольник АВН, тем самым «перекроим» параллелограмм фигуру НВСК, из каких многоугольников состоит она?

Что можно сказать о фигурах ABCD и HBCK?

Чем является фигура НВСК?

Чему равна площадь НВСК?

Каким отрезком параллелограмма можно заменить отрезок НК?

И так , чему равна площадь ABCD?

Какой вывод мы можем сделать из проведенного исследования, как же найти площадь параллелограмма ABCD?

Сторону AD параллелограмма называют основанием. А если в качестве основания взять сторону CD и провести к ней высоту ВК, то как мы найдем площадь параллелограмма?

Еще раз прослушаем доказательство теоремы: «Площадь параллелограмма равна произведению длины стороны параллелограмма на высоту, проведенную к этой стороне». Учитель проводит еще раз доказательство по рисунку

Работа в группах (перекраивают параллелограмм в прямоугольник).

Решение поставленной задачи проводится совместными исследованиями и обоснованиями учителя и учащихся, используя наглядные возможности анимации.(Слайд 9 ).

Они равны как противоположные стороны параллелограмма.

Они прямоугольные и равны по гипотенузе и острому углу.

Их площади равны.

Из трапеции HBCD и треугольника ABH.

Из трапеции HBCD и треугольника DCK.

Они равновелики по разложению, значит, их площади равны.

Прямоугольником, так как это параллелограмм с прямыми углами.

Произведению длин НК и ВН- смежных сторон прямоугольника.

Отрезком AD. Так как HK=BC=AD.

Произведению длин отрезков AD и BH.

Провести высоту ВН и найти произведение длин отрезков AD и BH.

Площадь параллелограмма равна произведению длины его стороны на высоту, проведенную к этой стороне. ( Слайд 10)

Смотрят на слайд и слушают, задают вопросы.

Предметные: умение выводить формулу для вычисления площади параллелограмма.

Регулятивные: планирование,

прогнозирование.

Познавательные: моделирование ситуации, построение логической цепи рассуждений, выдвижение гипотез и их обоснование,

Доказательство теоремы.

Коммуникативные: сотрудничество в поиске и выборе способа решения возникшей проблемы.

Физминутка

Слайд

Цель этапа

зафиксировать изученное учебное содержание.

6. Диагностика качества учебно-познавательной деятельности

Организует деятельность по применению новых знаний в виде обучающей самостоятельной работы.

Возьмите лист с печатной основой и докажите теорему о площади параллелограмма.

Выполняют самостоятельную работу.

Записывают на листе с печатной основой доказательство теоремы

Личностные: самоопределение. Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения.

Цель этапа:

1) зафиксировать новое содержание, изученное на уроке;

2) оценить собственную деятельность на уроке;

3) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;

4) обсудить и записать домашнее задание.

8. Рефлексия деятельности.

Организует рефлексию. Слайд

Осуществляют самооценку собственной учебной деятельности, соотносят цели и результаты, степень их соответствия.

Личностные: смыслообразование.

Познавательные: рефлексия

Коммуникативные: умение с

достаточной полнотой и

точностью выражать свои мысли.

7. Запись домашнего задания

Записываем в дневник домашнее задание

№459, п 52

Записывают в дневник домашнее задание.

Личностные: самоопределение. Регулятивные: контроль, коррекция.