- Учителю
- Урок по математике для 8 класса «Теорема Виета»
Урок по математике для 8 класса «Теорема Виета»
Конспект урока по математике в 8 классе «Теорема Виета»
Цель урока: Изучить теорему Виета и обратную ей теорему
Ход урока.
1 Этап подготовки к изучению нового материала.
Совместное обсуждение следующих вопросов:
Какую тему мы изучаем? Какие способы решения квадратных уравнений вы знаете? Какое уравнение называется приведенным? Что такое p и q?
Сегодня мы научимся решать приведенные квадратные уравнения еще одним способом.
Задание классу. Работа в парах.
Решите уравнения и заполните карточки (Карточки выдаются по одной на парту)
Уравнение
p
q
x1 +x2
x1x2
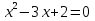
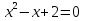
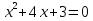
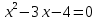
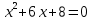
Проверка с помощью презентации или документ - камеры.
Уравнение
p
q
x1 +x2
x1x2
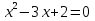
- 3
2
3
2
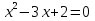
-1
- 2
1
-2
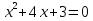
4
3
-4
3
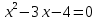
- 3
- 4
3
- 4
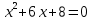
6
8
- 6
8
Не заметили ли вы какой -то закономерности?
Запишем вывод: 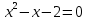
Как вы думаете, для всех уравнений выполняются эти соотношения? Можем мы проверить все уравнения? Значит, надо доказать.
2. Этап изучения нового материала.
Докажем. 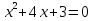 . Мы знаем, что
. Мы знаем, что 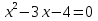 ,
, 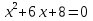 . Найдите самостоятельно
. Найдите самостоятельно 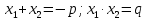
Смотрим у кого получилось. ( Проверяем через документ камеру)
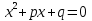
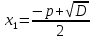
Мы с вами доказали теорему Виета: Если х1 и х2 корни квадратного уравнения, то 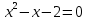 .
.
Виет - великий французский ученый, нас познакомит с ним …… Один из учеников выступает с сообщением о Франсуа Виете.
Учитель формулирует теорему обратную теореме Виета и предлагает учащимся ее доказать. Если числа m и n таковы, что m+n=-p и mn=q, то m и n корни квадратного уравнения 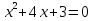 .
.
Доказательство
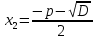
Раскроем скобки, сгруппируем слагаемые и разложим левую часть на множители
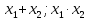
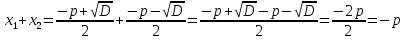
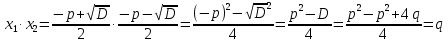
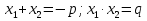
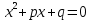
Что и требовалось доказать.
3. Этап первичного закрепления.
С помощью теоремы, обратной теореме Виета, можно устно находить корни квадратного уравнения. Попробуем. Записываем формулы и находим корни следующих трех уравнений.
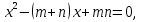 ,
, 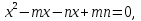 ,
, 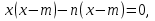
Какие вопросы у вас сейчас возникли?
-
А если числа большие?
-
А если корней нет? Как определить?
-
А если один корень?
-
А если уравнение не приведенное? Для него выполняется? (Можно привести) Формулируем теорему в общем случае.
Теорема Виета имеет очень широкое применение. Вот только несколько примеров.
Решить устно:
-
Найдите сумму и произведение корней уравнения
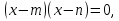
-
Верно ли решено уравнение?
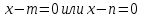
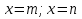
-
Составьте уравнение по его коням
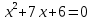
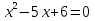
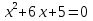
Получим уравнение 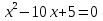
4 этап. Формулируем разноуровневое домашнее задание.
5 этап. Рефлексия.
Подводим итог урока. Продолжите предложения
Сегодня на уроке я узнал…
Сегодня на уроке я научился…
Сегодня на уроке я познакомился…