Разработка урока по геометрии на тему 'Медианы биссектрисы и высоты треугольника' (7 класс)

План-конспект

Тема: Медианы биссектрисы и высоты треугольника

Класс: 7

Тип урока: урок ознакомления с новым материалом

Методы: словесные, наглядные, практические, самостоятельной работы, фронтального опроса, контроля и оценки

Оборудование: раздаточный материал

Цель: выработать умение строить медианы, биссектрисы и высоты треугольника.

Задачи:

Образовательные:

• ввести понятие перпендикуляра к прямой, медианы, биссектрисы и высоты треугольника;

• сформировать умение строить медианы, биссектрисы и высоты треугольника.

Развивающие:

• развивать познавательный интерес и логическое мышление;

• развивать умение видеть проблему и выдвигать гипотезы по ее решению;

• развивать навыки коллективной работы учащихся в сочетании с самостоятельным умением анализировать, выделять главное, обобщать и делать выводы

Воспитательные:

• создать условия для воспитания коммуникативных навыков и навыков сотрудничества;

• вовлечь в активную деятельность всех учащихся класса;

• воспитывать у учащихся любознательность.

Структура урока

1. Организационный момент.

2. Проверка домашнего задания.

3. Повторение ранее изученного материала.

4. Изучение нового материала.

5. Закрепление изученного материала.

6. Подведение итогов урока.

7. Постановка домашнего задания.

Ход урока

1. Организационный момент.

Проверить готовность учащихся к уроку. Сформулировать тему и цели урока.

2. Проверка домашнего задания.

3. Повторение ранее изученного материала.

Геометрический марафон

а) Перпендикулярные прямые

б) Треугольник

в) Вертикальные углы

г) Тупой угол

д) Луч

е) Отрезок

ж) Острый угол

з) Точка

и) Развернутый угол

к) Смежные углы

л) Прямой угол

м) Биссектриса

н) Прямая

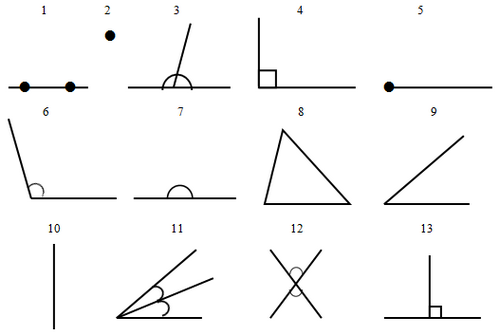
Ответы: е , з , к , л , д , г , и , б , ж , н , м , в, а .

Ответьте на вопросы:

1) А что называется треугольником? (Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых попарно отрезками).

2) Назовите элементы треугольника. (Три вершины, три стороны и три угла).

3) Какие виды треугольника вы знаете? (прямоугольный, равнобедренный, равносторонний)

4. Изучение нового материала.

1. Введение понятия перпендикуляра к прямой.

Практическая работа:

Начертите прямую а и отметьте точку А, не лежащую на этой прямой. (Аа)

Через точку А проведите прямую, перпендикулярную прямой а. Точку пересечения прямых обозначьте Н. (АН  а)

Как называются прямые АН и а? Запишите взаимное расположение прямых с помощью математических символов.

Подумайте, как может называться отрезок АН?

Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны.

А

а

Н

Сколько отрезков, удовлетворяющих нашему условию, можно провести к прямой а?

Теорема о перпендикуляре:

Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Работа по слайдам 5-8.

2. Введение понятия медианы треугольника

Постройте треугольник АВС. На стороне ВС поставьте точку М так, чтобы она являлась серединой отрезка. Соедините точки А и М. Отрезок АМ является медианой треугольника АВС.

А

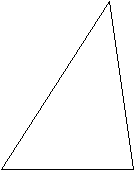
С М В

АМ - медиана треугольника

Дайте определение медианы треугольника. Сверим Ваше определение с определением записанным в учебнике на стр. 44.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

Сколько медиан можно провести в треугольнике?

3. Введение понятия биссектрисы

Постройте треугольник АВС. В треугольнике угол ВАС поделите лучом АА₁ пополам. Отрезок АА₁ является биссектрисой треугольника АВС.

А

С А₁ В

АА₁ - биссектриса треугольника

АСА = ВАА

Дайте определение биссектрисы треугольника. Сверим Ваше определение с определением записанным в учебнике на стр. 44.

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

Попросить учащихся выполнить построение биссектрис треугольника на листе контроля.

Сколько биссектрис можно провести в треугольнике?

4. Введение понятия высоты треугольника

Постройте треугольник АВС. Из вершины А на сторону ВС опустите перпендикуляр АН. Отрезок АН является высотой треугольника АВС. (АН  СВ)

А

С Н В

АН - высота треугольника

Дайте определение высоты треугольника. Сверим Ваше определение с определением записанным в учебнике на стр. 44.

Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

Сколько высот можно провести в треугольнике?

Физкультминутка

1. Потереть ладонью о ладонь. Закрыть глаза и положить ладони на них. Отдых 10-15 с.

2. Быстро поморгать глазами. Закрыть глаза. Отдых 10-15 с.

3. Открыть глаза.

Практическая работа

Работа проводится в парах по рядам на раздаточном материале.

Задание:

I ряд в треугольнике с помощью масштабной линейки проводит медианы треугольника.

II ряд в треугольнике с помощью транспортира и линейки проводит биссектрисы треугольника.

III ряд в треугольнике с помощью чертежного треугольника проводит высоты треугольника.

При этом учащиеся, сидящие за первыми партами работают с остроугольным треугольником, за вторыми партами - с прямоугольным треугольником, за третьими

партами - с тупоугольным треугольником, далее распределение по рядам продолжается в этом же порядке.

Примечание: при построении высот в тупоугольном треугольнике можно получить консультацию у учителя.

Выводы:

1. Учащиеся I ряда прикрепляют на доске получившиеся построения медиан в треугольниках.

Какой вывод можно сделать? Медианы в треугольнике пересекаются в одной точке.

В любом треугольнике медианы пересекаются в одной точке.

Точку пересечения медиан (в физике) принято называть центром тяжести

2. Учащиеся II ряда прикрепляют на доске получившиеся построения биссектрис в треугольниках.

Какой вывод можно сделать? Биссектрисы в треугольнике пересекаются в одной точке.

В любом треугольнике биссектрисы пересекаются в одной точке.

Точка пересечения биссектрис треугольника есть центр вписанной в треугольник окружности.

3. Учащиеся III ряда прикрепляют на доске получившиеся построения высот треугольника.

Какие трудности возникли при построении высот в треугольнике? Возникла проблема: как построить высоты из острых углов тупоугольного треугольника.

Какой вывод можно сделать? Высоты в треугольнике или их продолжения пересекаются в одной точке.

Точку пересечения высот называют ортоцентром.

4. Общий вывод

Каким замечательным свойством обладают медианы, биссектрисы и высоты треугольника?

5. Закрепление изученного материала.

1)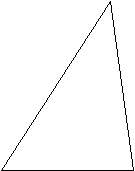

Задание: с помощью чертежных инструментов найдите на рисунке: а) медиану; б) биссектрису; в) высоту треугольника MKT.

а) Медиана - отрезок ВТ.

б) Биссектриса - отрезок АК.

в) Высота - отрезок СМ.

2) а) Назвать элемент и дать его определение

б) Проверочная работа.

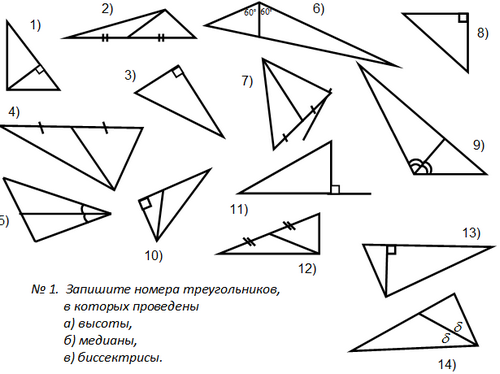
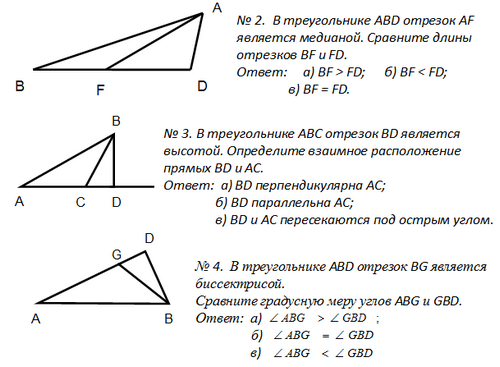
6. Подведение итогов урока.

Повторить основные понятия, изученные на уроке.

Продолжи фразу: я сегодня на уроке … .

7. Постановка домашнего задания. § 11, знать основные определения и формулировки утверждений и теорем, №135.

Лист контроля

Ф.И._____________________________

1. Геометрический марафон.

2. Построение

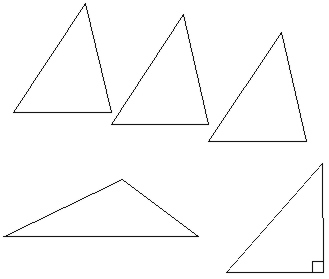
3. Проверочная работа

1) а)__________________

б)__________________

в)___________________

2) _____

3) _____

4) _____