Конспект урока геометрии по теме 'Параллельный перенос' 9 класс

Цели урока: слайд 2

• Закрепить знания по осевой и центральной симметрии. Установить что такое параллельный перенос. Учиться выполнять параллельный перенос и применять его при решении задач.

• 2. Развивать логическое мышление, умение доказательно развивать свою мысль и умение делать выводы.

• 3. Формирование умения работать в коллективе. Воспитывать умение делать собственный выбор. Воспитание любви к природе и Родине.

Тип урока: урок усвоения нового материала.

Оборудование:

1. карточки-задания;

2. учебник геометрии 7-9 классов Л.С.Атанасяна;

3. мультимедиапроектор (презентация по теме урока).

Ход урока.

I. Организационный момент. Проверка готовности класса к уроку.

Французский писатель 19 века Анатоль Франс однажды заметил:

«Учиться можно только весело. Чтобы переварить знания, надо поглощать их с аппетитом». слайд 3

Сегодня мы последуем совету писателя и будем с желанием поглощать знания, которые пригодятся нам в будущем.

II. Проверка домашнего задания. Фронтальный опрос. слайд 4

Давайте повторим всё, что мы узнали о движении, об осевой и центральной симметриях.

• Дайте определение движения.-

-Движение - отображение плоскости на себя, сохраняющее расстояние.

• Назовите свойства движения.

-При движении:

отрезок отображается на равный ему отрезок

треугольник отображается на равный ему треугольник

угол отображается на равный ему угол

луч отображается на луч

прямая отображается на прямую

любая фигура отображается на равную ей фигуру

• Являются ли осевая и центральная симметрия движением? слайд 5

-Осевая и центральная симметрия - движения.

• .Что называется осевой симметрией?

-Преобразование, при котором каждая точка фигуры преобразуется в симметричную ей относительно некоторой оси точку, называется

осевой симметрией или симметрией относительно прямой

• Что называется центральной симметрией?

-Преобразование, переводящее каждую точку фигуры в точку , симметричную ей относительно центра О, называется центральной симметрией или симметрией относительно точки.

Точка О называется центром симметрии и является неподвижной.

Других неподвижных точек это преобразование не имеет.

Теперь открыли тетради и дневники

III. Задание на дом: слайд 6

Запишите домашнее задание: п.116, вопросы 14, 15 (стр. 281), №1163(а), №1165. Принести циркуль и транспортир к следующему уроку.

IV. Математический диктант. слайд 7

Подпишите в тетрадях число. А теперь практическая проверка ваших знаний:

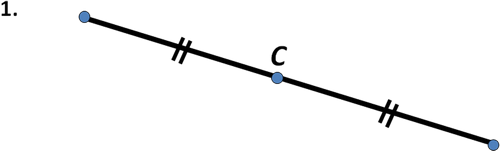
1.Отметьте точки Р и С. Постройте точку Р₁, симметричную точке P относительно точки С.

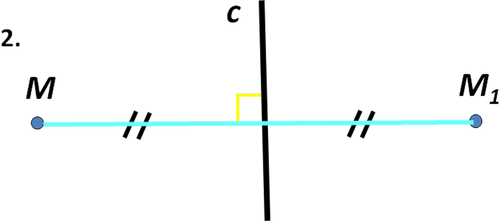
2. Начертите прямую с и точку М вне ее. Постройте точку М₁, симметричную точке М относительно прямой с

3.Закончите предложение:

«Преобразование фигуры F в фигуру F₁ называется движением, если оно ...».

4. Треугольники NCL и МКР симметричны относительно некоторой точки. Стороны ΔNCL равны 5 см, 9 см и 11 см. Найти периметр Δ МКР.

5. В какую фигуру переходит при движении отрезок длиной в 5 см?

V. Взаимопроверка диктанта. (слайд 8 - 9 - 10)

Поменяйтесь тетрадями в парах. Ответы вы видите на слайдах.

3. …если оно сохраняет расстояние»

4. 25 см

5. в отрезок длиной 5 см

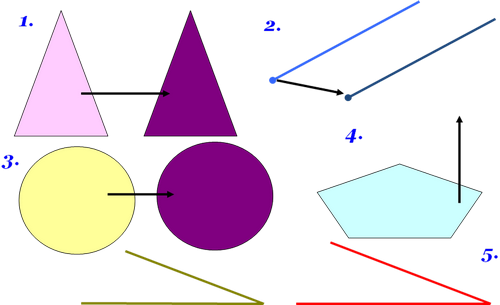
Ребята, как вы думаете, в какую фигуру при движении отображается:

1. Треугольник?

2. Луч?

3. Окружность?

4. Пятиугольник? и

5. Угол?

VI Актуализация опорных знаний (повторение пройденного материала)

Перед тем, как приступить к изучению темы урока, давайте вспомним:

1. Какие прямые называются параллельными?
2. Признак параллелограмма. (Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм).
3. Свойство сторон параллелограмма. (В параллелограмме противоположные стороны равны).
4. Что такое вектор?

Направленный отрезок, для которого указано начало и конец.

VII. Изучение новой темы. слайд 11

Запишите в тетради тему урока:«Параллельный перенос».

Что знакомо в названии?

Итак, предоставляется слово (ученик…), который подготовил нам объяснение данной темы.

-Определение: Преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении на одно и то же расстояние, называется параллельным переносом.

Чтобы задать преобразование параллельного переноса, достаточно задать вектор а ).

Докажем, что параллельный перенос - движение.

Параллельный перенос является движением т.е. отображение плоскости на себя, сохраняющим расстояния. Чтобы задать параллельный перенос достаточно указать: 1) направление 2) расстояние - слайд 12 - 16

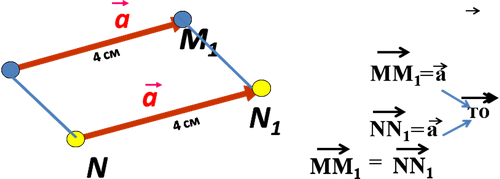
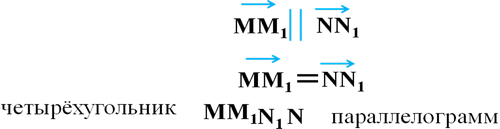
Для параллельного переноса имеют место следующие свойства:

1) отрезок переходит в равный ему отрезок;

2) угол переходит в равный ему угол;

3) окружность переходит в равную ей окружность;

4) любой многоугольник переходит в равный ему многоугольник;

5) параллельные прямые переходят в параллельные прямые;

6) перпендикулярные прямые переходят в перпендикулярные прямые.

VIII. Закрепление темы слайд 17 - 19

Решим № 1162, 1163(а), 1164

IX. Разноуровневая практическая работа.

А. Начертите отрезок АВ и вектор СС₁. Постройте отрезок А₁В₁, который получится из отрезка АВ параллельным переносом на вектор СС₁.

В. Начертите ΔАВК и вектор ММ₁. Постройте ΔА₁В₁К₁, который получится из ΔАВК параллельным переносом на вектор ММ₁.

С. Начертите пятиугольник МКРВТ и вектор АА₁. Постройте пятиугольник М₁К₁Р₁В₁Т₁, который получится из МКРВТ параллельным переносом на векторАА₁.

X.Рефлексия.

Ваше мнение об уроке…

Всё ли тебе было понятно…

Что было непонятно…

XI. Итог урока.

Какое отображение плоскости называется параллельным переносом?

Приведите примеры из жизни, где вы встречались с параллельным переносом.

Оценивание учащихся.