- Учителю
- Урок по алгебре в 11 классе по теме «Иррациональные уравнения»
Урок по алгебре в 11 классе по теме «Иррациональные уравнения»
Открытый урок по алгебре и началам анализа
в 11 «А» классе
Учитель: Дробышевская Л.А.
Тема урока: Иррациональные уравнения.
Цели урока: а) организовать работу учащихся по усвоению определения иррационального уравнения, изучению способов его решения; формировать умения учащихся решать иррациональные уравнения;
б) способствовать развитию мышления, памяти, внимания учащихся, умению самостоятельно добывать знания, способствовать развитию познавательных способностей учащихся;
в) воспитывать интерес учащихся к новым знаниям, настойчивость, дисциплинированность, ответственное отношение к учебному труду.
Эпиграф: «Считать несчастным тот день или тот час, в который ты не усвоил ничего нового, ничего не прибавил к своему образованию».
Ян Амос Коменский
План урока.
I. Организационный момент
II. Постановка цели урока.
III. Актуализация опорных знаний.
IV. Изучение нового материала.
V. Формирование навыков решения иррациональных уравнений.
VI. Контроль усвоения (устная работа).
VII. Домашнее задание.
VIII. Итог урока. Рефлексия.
Ход урока.
I. Организационный момент
Звучит негромкая музыка. Учитель читает стихотворение:
-- О, математика земная! Я славлю разум человека,
Светило всех земных светил. Дела его волшебных рук,
Тебя царицей величавой Надежду нынешнего века, Недаром Гаусс окрестил. Царицу всех земных наук!
II. Постановка цели урока.
-- В предыдущих классах вы решали линейные, квадратные, дробно-рациональные уравнения. Сегодня на уроке мы познакомимся с новым видом уравнений: иррациональными уравнениями. (Тема, эпиграф, задания записаны на доске). Вы должны усвоить определение иррационального уравнения, познакомиться со способами решения и научиться решать иррациональные уравнения.
III. Актуализация опорных знаний.
― Для того чтобы легче было работать на уроке, давайте повторим нужные нам сведения.
1.Вопросы ученикам:
―Что значит решить уравнение?
―Что такое корень уравнения?
―Какие уравнения называются равносильными?
―Как по-другому называется знак корня?
―Замените следующие корни степенью с дробным показателем: ![]() ,
,![]() ,
, ![]()
― Как возвести степень в степень?
2. Решить устно:
![]() А)
А)![]() Ответ: Г)
Ответ: Г) ![]() ‾ 5х + 6 = 0 Ответ:
‾ 5х + 6 = 0 Ответ: ![]()
![]()
![]() Б)
Б) ![]() Ответ: Д)
Ответ: Д) ![]() Ответ:
Ответ: ![]() ,
, ![]()
![]() В)
В) ![]() Ответ: Е)
Ответ: Е) ![]() Ответ:
Ответ: ![]() ,
, ![]()
3. Восстановите формулу:
1) ![]()
![]()
2) ![]()
![]()
3) ![]()
![]()
4) ![]()
![]()
IV. Изучение нового материала.
― Знаете ли вы, какие уравнения называются иррациональными?
― Откройте учебник и прочитайте в §6 определение иррационального уравнения.
― Так какое же уравнение называется иррациональным?
― Приведите примеры иррациональных уравнений.
― Какие, из записанных на доске уравнений, иррациональные?
1)![]() 5)
5) ![]()
2) ![]() 6)
6)![]()
3)![]() 7)
7) 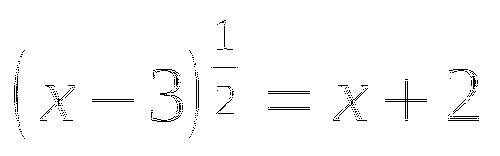
4)![]() 8)
8) 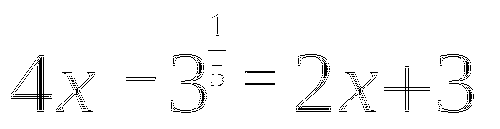
(Ответ: 1), 4), 5), 6).)
― При решении иррациональных уравнений необходимо иметь в виду, что радикалы с чётными показателями и их подкоренные выражения неотрицательны, подкоренное выражение радикала с нечётным показателем может быть любым действительным числом, знак радикала при этом совпадает со знаком подкоренного выражения.
―Как вы думаете, почему не имеет смысла приступать к решению уравнения ![]() ?
?
(Радикал с чётным показателем не может быть отрицательным числом.)
― Объясните, следует ли решать уравнения и почему?
1) ![]() (нет), 2)
(нет), 2)![]() (нет),
(нет),
3)![]() (нет), 4)
(нет), 4)![]() (да).
(да).
― Итак, последнее уравнение нужно решать.
― Какие же существуют способы решения иррациональных уравнений?
― Найдите ответ в учебнике и назовите эти способы.
(1. Возведение в степень. 2. Введение новой переменной.)
Объяснение способов решения иррациональных уравнений учителем.
― Решим следующие уравнения:
1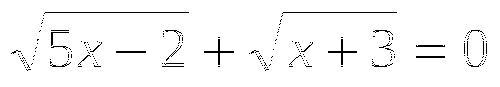 )
)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
.
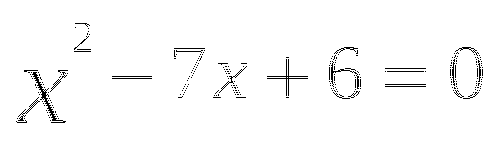
2)
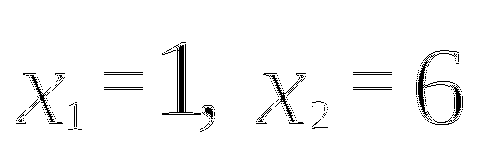
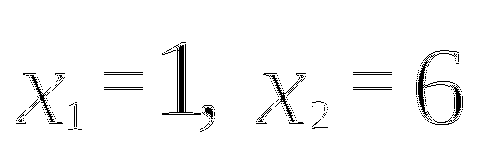
3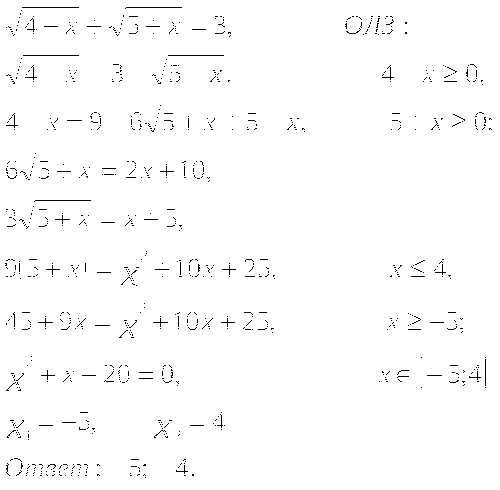 )
)
V.Формирование навыков решения иррациональных уравнений.
(Вызванные ученики решают у доски по одному примеру с комментариями, остальные ведут записи в тетрадях.)
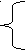
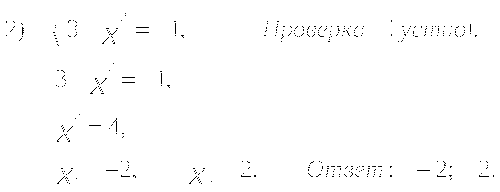
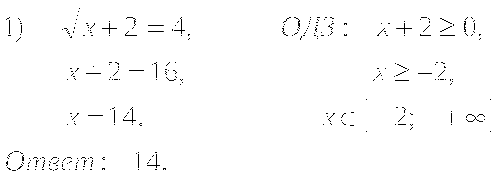
VI. Контроль усвоения (устная работа).
-
Какие из следующих уравнений являются иррациональными:

-
Решите устно:
![]()
VII. Домашнее задание.
§6, № 96 (2, 4), № 97 (2, 4).
VIII. Итог урока. Рефлексия.
―П родолжите фразу: «Сегодня на уроке я узнал(а)…».
родолжите фразу: «Сегодня на уроке я узнал(а)…».
«Сегодня на уроке я познакомился (лась)…».
«Сегодня на уроке я научился (лась)…»